P4967 黑暗打击 题解

P4967 黑暗打击 题解

题目

洛谷 P4967 黑暗打击

声明

由于本人实在是太菜，所以做这道题的时候还去看了好多相关的博客，也参考了洛谷上前几篇题解的一些思路，在此对写前几篇题解的巨佬表示感谢。

分析

这道题有很强的递推性，而数据范围又很大，所以我们首先想到了用矩阵加速来做这道题，但是 $10^{10000}$ 的数据范围还是会让朴素的矩阵过不了~~（何况你也不想去写高精吧）~~，所以我们还需要用到指数循环节定理，这样时间复杂度就能降能过的程度了。

过程

前置知识

我们先简简单单地讲一下解决本题需要运用到的矩阵加速以及指数循环节定理（如果您会可以直接跳过这一部分）。

矩阵加速

线性代数研究的向量多为列向量，根据这样的对矩阵乘法的定义方法，经常研究对列向量左乘一个矩阵的左乘运算，同时也可以在这里看出“打包处理”的思想，同时处理很多个向量内积。

矩阵乘法满足结合律，不满足一般的交换律。

利用结合律，矩阵乘法可以利用快速幂的思想来优化。

在比赛中，由于线性递推式可以表示成矩阵乘法的形式，也通常用矩阵快速幂来求线性递推数列的某一项。

——引用自oi-wiki

如上文所写，我们可以将每阶的“希尔伯特曲线土壤”存储在一个矩阵中，使用这个矩阵乘上状态转移矩阵的 $n$ 次方就可以得到 $n$ 阶“希尔伯特曲线土壤”的状态了。如果想要详细了解矩阵加速，请参阅oi-wiki，如果您看不懂也可以去搜博客。

欧拉函数

讲欧拉函数是为了方便各位理解指数循环节定理。最简单地来讲，$n$ 的欧拉函数表示为 $\phi (n)$，其意义为 $1\sim (n-1)$ 中与 $n$ 互质的数的个数。如果要详细了解，我推荐这篇博客。

指数循环节

我们在这里直接放出公式，想要看详细证明可以看这篇博客。
$$a^b\equiv a^{b\%\phi (m)+\phi (m)}(\mathrm{mod}m)$$

转移矩阵推导

为了推导这道题，我们先画出几张“希尔伯特曲线土壤”的图，其中蓝色表示水能淹到的区域，橙色表示不能淹到的区域（由于是用画图一个一个像素画的，所以每个格子的大小是和墙壁一样宽的，可能会出现一点变形。

由于前几个矩阵太小，不具有多少推导价值，所以我们从 $4$ 阶开始。

$4$ 阶希尔伯特曲线土壤

$5$ 阶希尔伯特曲线土壤

$6$ 阶希尔伯特曲线土壤

我们观察到，一个希尔伯特曲线土壤按照被淹的数量可以被分成大致四个部分。以 $6$ 阶希尔伯特曲线土壤为例：

▓ 蓝色 上一阶希尔伯特曲线土壤中上面一半的部分

▓ 红色 上一阶希尔伯特曲线土壤中下面一半的部分

▓ 绿色 没有被灌水的部分

▓ 黄色 几块中间被灌满水的部分

我们可以发现，每个希尔伯特曲线土壤就可以由上一个希尔伯特曲线土壤转移而来，而每一小段黄色部分被灌水的面积就是 $2^n$ 或 $2^n-1$！

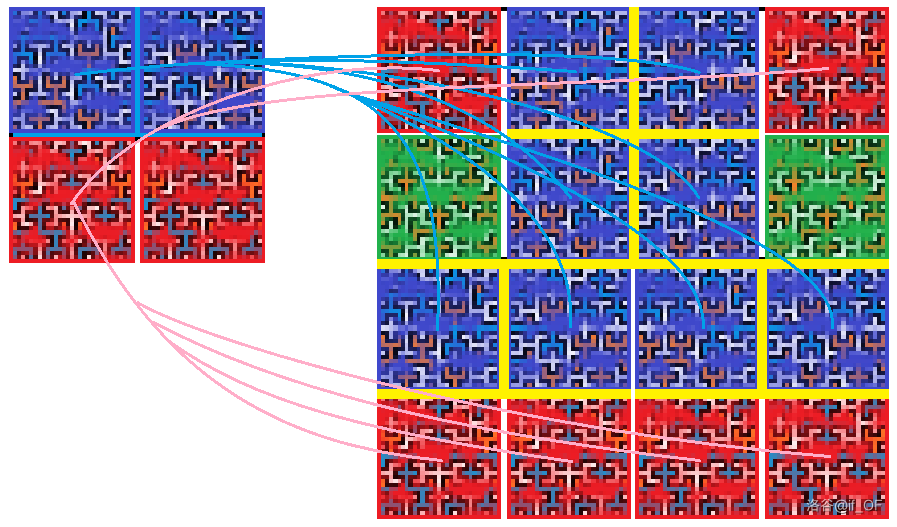
于是，我们用一个 $1\times 4$ 的矩阵存储每阶希尔伯特曲线土壤的上面的一半、下面的一半、中间间隔的部分还有 $1$。

什么？你问我为啥要浪费那一点点空间去存个 $1$？因为上面已经说过，每个黄色部分的长度不全是 $2^n$。比如下图：

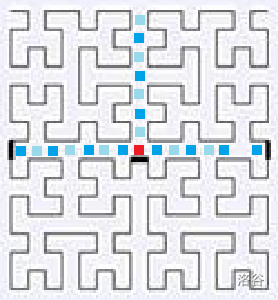
接下来，我们就可以运用前后两个希尔伯特曲线土壤的 $1\times 4$ 矩阵来推出转移矩阵了。

我们设转移矩阵为 $C$，每个蓝色块为 $a$，每个红色块为 $b$，每个黄色块为 $c$ ，则有：
$$\left[\begin{array}{cccc}a& b& c& 1\end{array}\right]\times C=\left[\begin{array}{cccc}3a+1b+1c+-1& 2a+2b+3c-2& 2c& 1\end{array}\right]$$
于是，我们就可以算出 $C$ 矩阵为：
$$\left[\begin{array}{cccc}2& 2& 0& 0\\ 1& 2& 0& 0\\ 1& 3& 2& 0\\ -1& -2& 0& 1\end{array}\right]$$

利用指数循环节降低时间复杂度

$10^{10000}$ 是无论用啥都存不下来的，但是我们有之前讲到的指数循环节定理，于是我们就只需要用快读一遍读入，一边判断 $n$ 大于 $9223372036854775783$ 就让 $n$ 模上 $9223372036854775783-1$（因为 $9223372036854775783$ 是质数，所以它与小于它的所有数互质，于是 $\phi (9223372036854775783)$ 就等于 $9223372036854775783-1$），读完了再加上 $9223372036854775783$ 就行了。

代码

#include<bits/stdc++.h>
#define lll __int128//由于取模的数字本身就已经接近long long的上限，所以只能用int128来存矩阵 
#define ll long long
using namespace std;
const int MAXN=105;
long long MOD=9223372036854775783;
lll getnum()//快读 
{
	lll x=0;
	int f1=1 , f2=0;//f1是记录有没有负号的（虽然本题用不到），f2是记录有没有大于过MOD 
	char c=getchar();
	while(c<'0' || c>'9')
	{
		if(c=='-')
			f1=-1;
		c=getchar();
	}
	while(c>='0' && c<='9')
	{
		x=(x<<1) + (x<<3) + (c^48);//等同于x=x*10+c-'0' 
		if(x>MOD)//用指数循环节定理进行优化 
			f2=1 , x=x%(MOD-1);
		c=getchar();
	}
	return f1*x + f2*(MOD-1);//如果x大于过MOD即用过指数循环节定理，x就需要加上MOD的欧拉函数 
}
void putnum(lll a)//快写 
{
	if(!a)
	{
		putchar('0');
		return;
	}
	int t=1;
	while(t<=a)
		t*=10;
	do
	{
		t/=10;
		putchar('0' + a/t%10);
	}while(t!=1);
}
struct Matrix
{
	lll val[MAXN][MAXN];
	int n,m;//矩阵的大小 
	Matrix()
	{
		memset(val,0,sizeof val);//清空矩阵 
	}
	void buildstd(int N)
	{
		for(int i=1 ; i<=N ; i++)
			val[i][i]=1;
		m=N , n=N;
	}//建立单位矩阵（任何矩阵乘对应的单位矩阵都等于它本身） 
};
Matrix operator *(const Matrix a,const Matrix b)//重载运算符实现矩阵乘法 
{
	Matrix ret;
	for(int i=1 ; i<=a.m ; i++)
	{
		for(int j=1 ; j<=b.n ; j++)
		{
			for(int k=1 ; k<=a.n ; k++)
			{
				ret.val[i][j]=(ret.val[i][j] + (a.val[i][k]%MOD)*(b.val[k][j]%MOD)%MOD )%MOD;//为了不超出范围，每步都要取模 
				if(ret.val[i][j]<0)	ret.val[i][j]+=MOD;//注意这个地方，因为我们的矩阵里有负数，我们需要给负数加上模数（取模意义下等于加0）让它变成正数 
			}
		}
	}
	ret.n=a.m,ret.m=b.n;
	return ret;
}
int main()
{
	Matrix A,B,ANS;
	lll n;
	A.m=1,A.n=4;//初始化第一个希尔伯特曲线土壤 
	A.val[1][1]=0,A.val[1][2]=0,A.val[1][3]=1,A.val[1][4]=1;
	B.m=4,B.n=4;//初始化转移矩阵 
	B.val[1][1]= 2,B.val[1][2]= 2,B.val[1][3]=0,B.val[1][4]=0;
	B.val[2][1]= 1,B.val[2][2]= 2,B.val[2][3]=0,B.val[2][4]=0;
	B.val[3][1]= 1,B.val[3][2]= 3,B.val[3][3]=2,B.val[3][4]=0;
	B.val[4][1]=-1,B.val[4][2]=-2,B.val[4][3]=0,B.val[4][4]=1;
	n=getnum();
	if(n==1)//特判 
	{
		puts("1");
		return 0;
	}
	ANS.buildstd(4);//建立单位矩阵 
	do
	{
		if(n&1)
			ANS=ANS*B;
		B=B*B;
		n>>=1;
	}while(n);//矩阵快速幂 
	A=A*ANS;
	printf("%lld\n",(long long)(A.val[1][2]%MOD));//转化为long long输出
	return 0;
}