b-树 b+树

b-树

举例，下图为一个5阶b-树（最下面的白色三岔符号表示叶子节点，该树的高度为4）

这里提一点，b-树的阶数是认为规定的，他不因树结点中的最大关键字数而改变，也不因结点的最大子树数而改变。

b-树的属性

1.一颗m阶的b-树，每个结点最多有m个子树；根节点切不为结点节点至少有两个子树，非根非叶结点至少有ceiling（m/2）个子树。

2.有n个子树的结点有n-1个关键字，他们按序排列（图中的树是递增的，递减也是允许的）。

3.叶子结点处于同一层（图中为第4层），可以用空指针表示，是查找失败到达的位置。

4.b-树按中序遍历得到的序列是有序的。

5.b-树中一个结点中的关键字个数为k，则子树个数为k+1。

一颗b-树实际上是这个样子的，他的每个节点最多能存放多少个关键字是确定的。

就算将（47，48，52，59）这一结点中删去一个关键字59，那么该树结点的最大关键字树变为3，那么该树依然是5阶b-树，树的阶数是不会变化的。

每个结点中存放的数据如上图所示，n表示当前节点能存放的关键字个数，key1到keyn表示n个关键字，p0到pn表示指向的子树结点。

b-树的查找

从根结点开始查找；

如果本节点中有目标关键字，查找成功；如果本节点没有目标关键字，则看目标关键字在本节点关键字划分的m个区间的哪个区间，随后在该区间对应的子树去查找；

循环上一步，如果到了叶子节点还没有查找成功，表示本b-树没有目标关键字，查找失败。

下图举例，在树中查找关键字35。先从根节点30下手，不匹配，在（>30）区间对应的的子节点查找；

结点中39，45 均不匹配，在（<39)对应的子结点去查找；

结点中33，34 均不匹配，在（>35)对应的子结点去查找；

到达叶子节点，说明本树中没有目标节点，查询失败。

b-的创建/插入关键字

用以下关键字序列｛1，2，6，7，11，4，8，13，10，5，17，9，16，20，3，12，14，18，19，15｝创建一棵5阶b-树。

前四个关键字，直接插入。

插入第五个时，结点中关键字会超出4，则取第ceiling(m/2)个关键字去上层（在这里ceiling(5/2)=3，取第三个数6）。

插入第六个关键字4时，先去查找4应该在哪个位置，发现应该在2的后面，并且该结点未达到4个关键字，可以直接插入。

同理，插入8。

插入13。

插入10，发现该结点超出m-1个关键字，去ceiling（m/2）位置的关键字10去上层。

继续插入5，17，9，16。

插入20时又超出上限，则取16去上层。

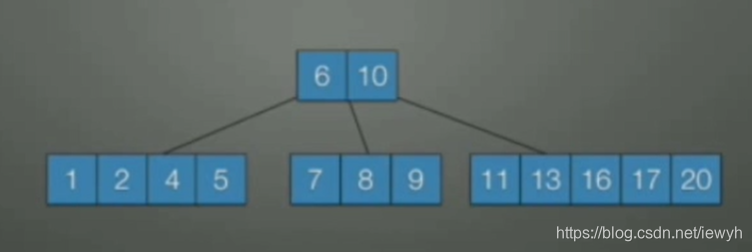
插入3，超出上限，取3去上层。

继续插入12，14，18，19

插入15时，超出上限，去13去上层。

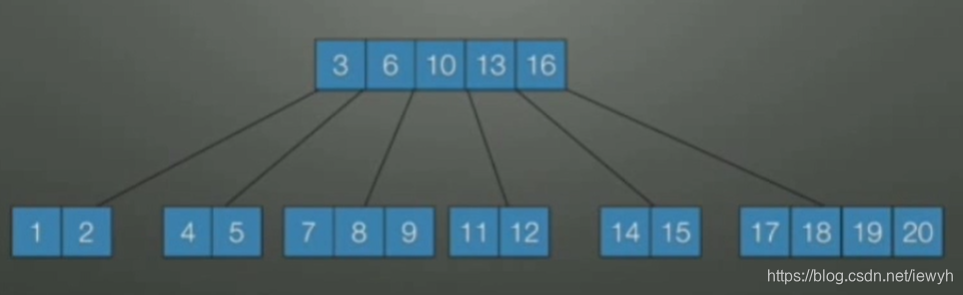
发现上层也超出上限，则再取10去更上一层

b-树的创建完成。

b-树删除关键字

还用这棵树举例，删除8，16，15，4这些关键字。

首先删除关键字8，删除后，结点中关键字个数符合要求。

删除16，删除后该结点个数小于2，不符合要求，这时我们需要先向下借结点，可以去向结点相邻的下层结点借最相近的关键字15或17，如果符合要求的话借15或17哪个都可以，不是唯一解。但是如果借15的话，则那个结点只剩下14不符合要求；如果借17的话，符合要求，就用17替代16的位置，删除成功。

接着删除15，删除后，该结点回不符合要求，并且它没有下层结点让他借，则考虑向兄弟节点借关键字，左右兄弟节点都可以借。但是由于左兄弟借完之后就不符合要求了，就向右兄弟借18。18上去替代17，17下来替代15，15就删除成功了。

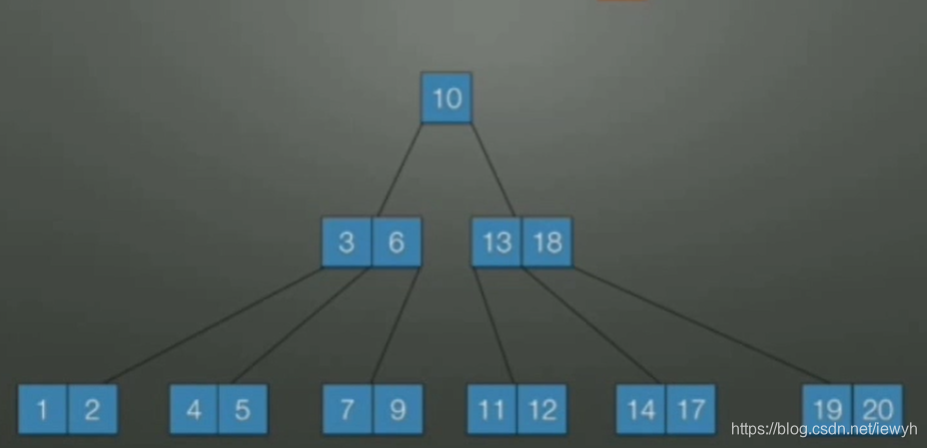
删除节点4，删除后结点不符合要求，去找下层结点发现没有，则去找兄弟结点借，但是左右兄弟都不借，这时我们考虑合并兄弟结点。由于左右借了之后都不符合要求了，所以我们合并左右兄弟节点都可以，先考虑合并左兄弟，3下来，删去4即可。

这时发现6这个节点也不符合要求了，就去找兄弟结点借，但是借不到，那么再次合并兄弟结点，10下来。

删除关键字14完成。

刚才是合并左兄弟结点，再来看看合并右兄弟结点。

还是删除4，合并右兄弟，那么就删除4，然后6下来。

这时3不符合条件了，则合并其右兄弟，10下来。

删除完成，我们发现合并左兄弟和合并右兄弟得到的结果是不一样的，删除结点的方法有很多，不是唯一的，只要符合要求就好。

b+树

属性：

1.b+树中，具有k个关键字的结点含有k个子树（对比b-树中具有k个关键字的结点含有k+1个子树）；

2.在m阶b+树中，每个结点的关键字个数最多为m，根节点非叶子结点关键字个数最少为2，非根非叶结点关键字个数最少为ceiling（m/2）（对比b-树，结点关键字最多m-1,根节点最少2，非根非叶结点最少ceiling（m/2）-1）；

3.在b+树中，最下一排包含关键字的结点中，包含了全部的关键字，叶子结点引出的指针指向记录；

4.b+树中所有非叶结点仅仅是一个索引，结点中的每个索引项只有对应子树的最大关键字和指向该子树的指针，不含有该关键字对应记录的存储地址（对比b-树，每个关键字对应一个记录的存储地址）；

5.b+树中，有一个指针指向关键字最小的叶子结点，所有叶子节点链接成一个线性链表。