1.游戏背景
《天之痕》是大宇旗下RPG游戏《轩辕剑》系列的第五部作品,该作于2000年12月在中国台湾地区发售,次年1月在中国大陆发售。《天之痕》以生动感人的故事、水墨风格的场景和凄美动听的音乐著称,游戏将古典美学发挥到了极致,树立了国产RPG游戏的标杆。
 游戏开始,主角陈靖仇随师傅陈辅至伏魔山寻找昆仑镜时,不慎放出了上古魔兽“饕餮”。陈辅将自己与其一同冰封于洞中,命陈靖仇到雷夏泽寻找公山师伯前来搭救。在雷夏泽,主线剧情完成后,可以和公山师伯的孙女公山梦玩猜数字小游戏,游戏规则如下:
游戏开始,主角陈靖仇随师傅陈辅至伏魔山寻找昆仑镜时,不慎放出了上古魔兽“饕餮”。陈辅将自己与其一同冰封于洞中,命陈靖仇到雷夏泽寻找公山师伯前来搭救。在雷夏泽,主线剧情完成后,可以和公山师伯的孙女公山梦玩猜数字小游戏,游戏规则如下:
 猜数字(又称Bulls and Cows)是一种起源于20世纪中期英国的密码破译类益智小游戏。通常由两个人玩,一方出数字,一方猜。出数字的人想好一个没有重复数字的4个数,不能让猜的人知道。猜的人每猜一个数字,出数者就要根据这个数字给出几A几B,其中A前面的数字表示位置正确的数的个数,而B前的数字表示数字正确而位置不对的数的个数。猜的人根据出题者的几A几B继续猜,直到猜中(即4A0B)为止。
猜数字(又称Bulls and Cows)是一种起源于20世纪中期英国的密码破译类益智小游戏。通常由两个人玩,一方出数字,一方猜。出数字的人想好一个没有重复数字的4个数,不能让猜的人知道。猜的人每猜一个数字,出数者就要根据这个数字给出几A几B,其中A前面的数字表示位置正确的数的个数,而B前的数字表示数字正确而位置不对的数的个数。猜的人根据出题者的几A几B继续猜,直到猜中(即4A0B)为止。
2.游戏实现
在《天之痕》中,游戏提示换成了几阳几阴,游戏规则其实还是一样的。我们编写一个程序来实现这个小游戏。
技术要点:生成四个不重复的数字、判定数字阳阴情况。
参考代码:
# -*- coding: utf-8 -*-
# @Date : 2025/07/05
# @Author : idsl2008
from random import sample
def analyse_number(secret, guess):
"""判定数字阳阴情况"""
yang, yin = 0, 0
for i, p in enumerate(secret):
for j, q in enumerate(guess):
if p == q and i == j: #数字正确且位置正确
yang += 1
elif p == q and i != j: #数字正确但位置不正确
yin += 1
return yang, yin
secret = sample('0123456789', k=4) #随机生成包含4个不重复数字的序列
n = 0
print("请连续输入四个不重复的数字,按回车键结束:\n")
while n < 10: #限定猜测次数
guess = input(">>>") #对输入的数字未作有效性和重复性检查
n += 1
yang, yin = analyse_number(secret, guess)
print("第%d次试猜结果:%d阳%d阴" %(n, yang, yin))
if yang == 4:
print("\n恭喜你在%d次内猜中秘密数字:%s,期待你的下次表现!" %(n, guess))
break
else:
print("\n很遗憾,你未能在10次内猜中秘密数字,请再接再厉!")
print("正确答案:", ''.join(secret))
运行结果:
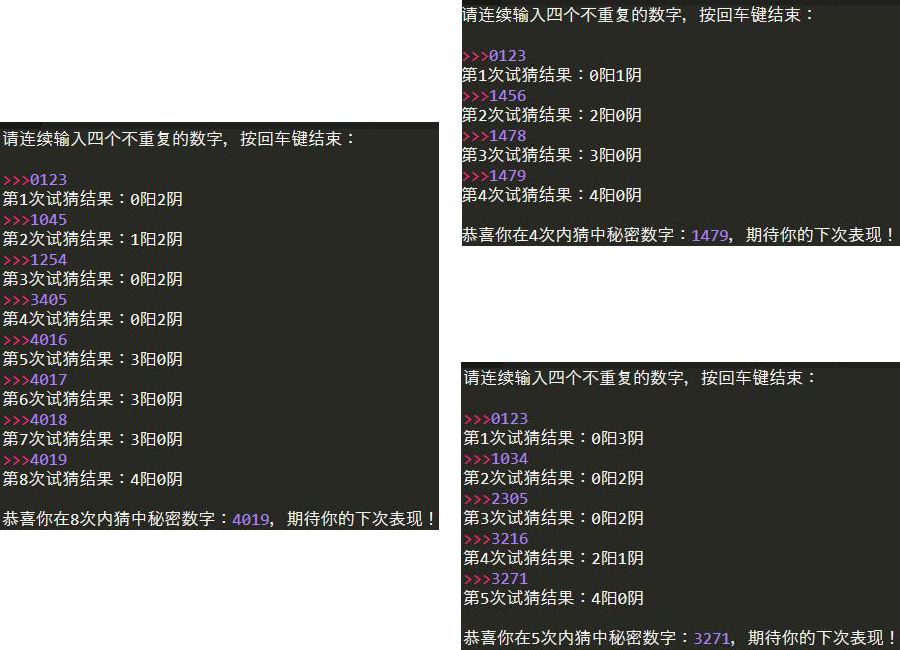
3.猜测策略
由于数字组合个数有限,每次猜测的选择有限,所以一定可以在有限次数内猜出正确答案。系统的猜测策略可分为三类:简单策略、启发式策略和最优策略。
简单策略每次都猜所有可能答案中的第一个,比如第一次就猜最小的数字0123。根据反馈,继续猜,如此多次,逐渐缩小可能集,直至猜出正确答案。简单策略的优点是速度快,缺点是所需猜测次数相对较多。
技术要点:枚举四个不重复数字从小到大所有排列、筛选符合阳阴条件的数字组合
参考代码:
# -*- coding: utf-8 -*-
# @Date : 2025/07/05
# @Author : idsl2008
from itertools import permutations
def analyse_number(secret, guess):
"""判定数字阳阴情况"""
yang, yin = 0, 0
for i, p in enumerate(secret):
for j, q in enumerate(guess):
if p == q and i == j: #数字正确且位置正确
yang += 1
elif p == q and i != j: #数字正确但位置不正确
yin += 1
return yang, yin
def guess_number(yang, yin):
"""筛选符合阳阴条件的数字组合(简单策略)"""
global array
temp = []
#将后续数字和第一个数字相比较,符合阳阴条件的数字加入新组合
for group in array[1:]:
s, t = analyse_number(array[0], group)
if s == yang and t == yin:
temp.append(group)
array = temp
array = list(permutations('0123456789', 4)) #枚举四个不重复数字从小到大所有排列
print("请连续输入猜测数字的阳阴结果,按回车键结束:\n")
print(''.join(array[0])) #第一次都猜0123
n = 1 #猜测次数
yang, yin = map(int, input(">>>"))
while yang < 4:
guess_number(yang, yin) #更新符合新一轮阳阴条件的数字组合
n += 1
print(''.join(array[0])) #提供新一轮试猜数字
yang, yin = map(int, input(">>>"))
print("\n正确答案:%s,猜测次数:%d" %(''.join(array[0]), n))
运行结果:
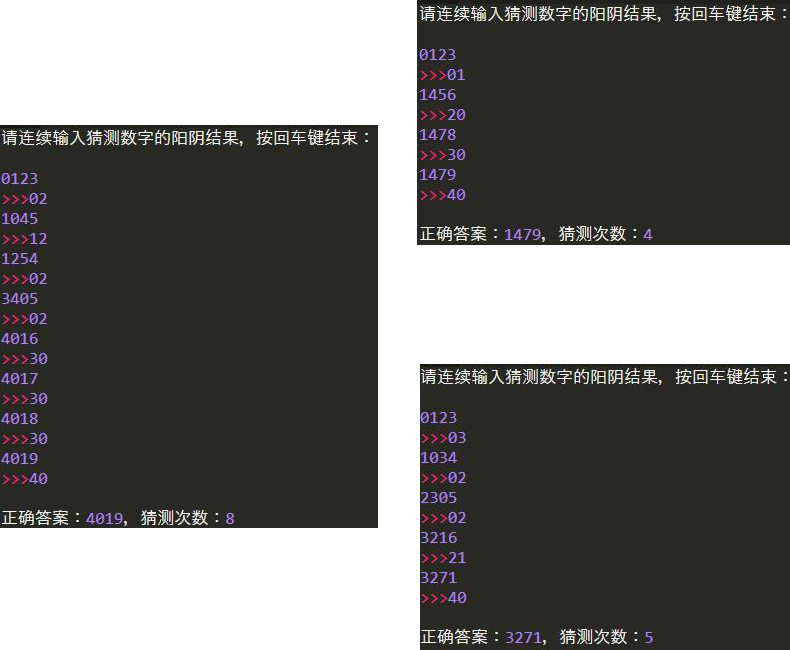
4.统计分析
如果进行5040次游戏,采用简单策略,平均猜测次数多少,猜测次数的频数分布又如何?想必通过上面的讲解,应该不难解决了吧
技术要点:统计频数、绘制直方图
参考代码:
# -*- coding: utf-8 -*-
# @Date : 2025/07/05
# @Author : idsl2008
from itertools import permutations
from random import sample
import pandas as pd
import matplotlib.pyplot as plt
def analyse_number(secret, guess):
"""判定数字阳阴情况"""
yang, yin = 0, 0
for i, p in enumerate(secret):
for j, q in enumerate(guess):
if p == q and i == j: #数字正确且位置正确
yang += 1
elif p == q and i != j: #数字正确但位置不正确
yin += 1
return yang, yin
def guess_number(yang, yin):
"""筛选符合阳阴条件的数字组合(简单策略)"""
global array
temp = []
#将后续数字和第一个数字相比较,符合阳阴条件的数字加入新组合
for group in array[1:]:
s, t = analyse_number(array[0], group)
if s == yang and t == yin:
temp.append(group)
array = temp
hist = {} #统计频数
count, total = 5040, 0 #游戏回合、所有回合总猜测次数
plt.rcParams['font.sans-serif'] = ['Microsoft YaHei'] # 使用微软雅黑字体
for i in range(count):
secret = sample('0123456789', k=4) #随机生成包含4个不重复数字的序列
array = list(permutations('0123456789', 4)) #枚举四个不重复数字从小到大所有排列
yang, yin = analyse_number(secret, array[0])
n = 1 #单回合猜测次数
while yang < 4:
guess_number(yang, yin) #更新符合新一轮阳阴条件的数字组合
n += 1
yang, yin = analyse_number(secret, array[0])
hist[n] = hist.setdefault(n, 0) + 1
total += n
avg = total / count
print("平均猜测次数:%.3f次" %avg)
df = pd.DataFrame(sorted(hist.items()), columns=['猜测次数', '频数'])
df.plot(kind='bar', x='猜测次数', y='频数', title='猜数结果分布图') #绘制直方图
plt.show()
运行结果:
平均猜测次数:5.541次
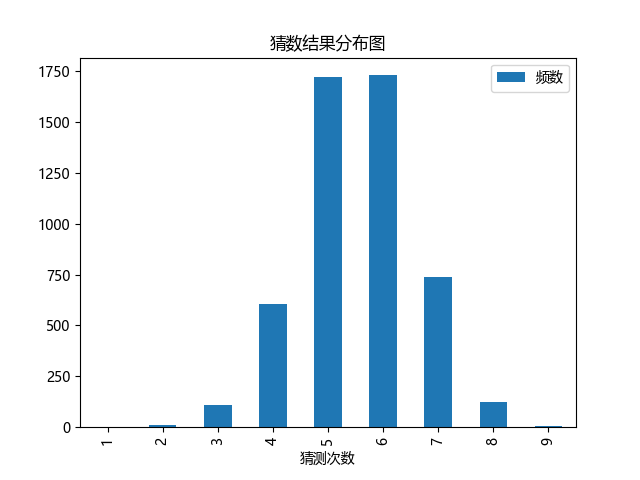
 《天之痕》猜数字游戏的实现与策略
《天之痕》猜数字游戏的实现与策略





















 4171
4171

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








