leetcode第4题 两个有序数组的中位数

题意： 给定两个有序数组 nums1，nums2， 找到这些数中的中位数。

第一种解法： 仿照桶排序的算法找到第K个数。时间复杂度 O(n). 空间复杂度 O(1)

class Solution {
public:
    double findMedianSortedArrays(vector<int>& nums1, vector<int>& nums2) {
        int m = nums1.size();
        int n = nums2.size();
        if (m > n) return findMedianSortedArrays(nums2, nums1);
        if ((m + n)%2){
            return findKthNum(nums1, nums2, 0, 0,(m + n)/2);
        } else {
            return (findKthNum(nums1, nums2, 0, 0, (m + n)/2-1) + findKthNum(nums1, nums2, 0, 0, (m + n)/2)) / 2.0;
        }
    }
    int findKthNum(vector<int>& nums1, vector<int>& nums2, int st1, int st2, int k) {
        while(k >= 0){
            int temp1 = INT_MAX;
            int temp2 = INT_MAX;
            if (st1 < nums1.size()) temp1 = nums1[st1];
            if (st2 < nums2.size()) temp2 = nums2[st2];
            if (temp1 <= temp2) ++st1;
            else ++st2;
            if (k == 0) return temp1 <= temp2? temp1:temp2;
            --k;
        }
        return 0;
        
    }
};

 

第二种解法： 上一种解法明显更加直观简单，但对于有序数组更快的查询思路应该采用二分法查找。时间复杂度O(lg n)。

这种时候可能不是很容易想出来如何在两个数组中二分。我们可以这样尝试分这两个数组。找到一个分界点index为 px和 py

使得 px + py  = (nums1.lsize() + nums2.size()) / 2。如果在这种情况下满足max_l1 <= min_r2 && max_l2 <= min_r1。那么我们最后就可以在中间这4个数中间找中位数。

• 
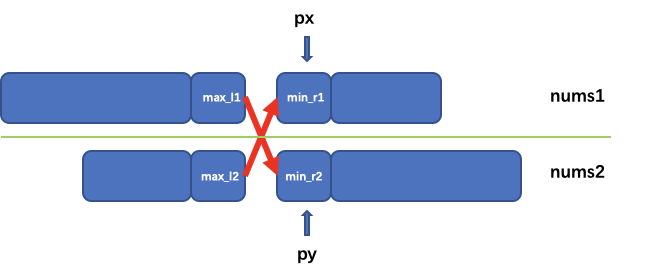
• 这个时候就可以尝试使用二分法查找px的位置。为了解决溢出情况我么可以假设每个数组开头有一个INT_MIN,结尾有一个INT_MAX。
• 代码如下：

class Solution {
public:
    double findMedianSortedArrays(vector<int>& nums1, vector<int>& nums2) {
        int m = nums1.size();
        int n = nums2.size();
        if (m > n) return findMedianSortedArrays(nums2, nums1);
        int st = 0;
        int en = m;
        while(st <= en){
            int px = (st + en) / 2;
            int py = (m + n) / 2 - px;
            
            int maxl1 = (px == 0)? INT_MIN : nums1[px-1];
            int minr1 = (px == m)? INT_MAX : nums1[px];
            
            int maxl2 = (py == 0)? INT_MIN : nums2[py-1];
            int minr2 = (py == n)? INT_MAX : nums2[py];
            
            if(maxl1 <= minr2 && maxl2 <= minr1){
                if ((m + n)%2 == 0){
                    return (max(maxl1, maxl2) + min(minr1, minr2)) / 2.0;
                } else {
                    return min(minr1, minr2);
                }
            } else if (minr1 < maxl2){
                st = px + 1;
            } else{
                en = px - 1;
            }            
        }
        return 0.0;
    }
};