数据结构与算法-排序算法（冒泡排序）

最新推荐文章于 2021-09-08 14:58:10 发布

iamsongyu

最新推荐文章于 2021-09-08 14:58:10 发布

阅读量1.1k

点赞数 4

CC 4.0 BY-SA版权

分类专栏：理论知识数据结构和算法

本文链接：https://blog.youkuaiyun.com/iamsongyu/article/details/99752601

理论知识同时被 2 个专栏收录

109 篇文章

订阅专栏

数据结构和算法

14 篇文章

订阅专栏

本文深入解析冒泡排序算法，通过实例展示排序过程，探讨时间与空间复杂度，并提供Java实现代码。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

排序是一个我们经常遇到的问题，这也是一个非常基本的问题，例如我们平时大小个站队？搜索数据之后的排序，常见的还是数字的排序等等（该图像素材来源于网络）

那么想象我们站队的时候是怎么排序的，来时看到谁最高就让谁站到第一位，然后再找第二高的，以此类推。我们看出高低也是互相比较得出的，计算机也可以使用这个方法，首先找到最高的，然后是第二高的，这种方法就是冒泡排序，因为他是按照大小一个一个的得到结果，就像是水泡浮出水面一样。

我们举一个简单的例子，

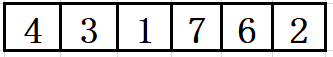
按照冒泡排序的原理，从第一位开始比较，4>3 所以换位置

然后是4和1比较，继续换位置

4<7 所以不用换位置最大的变为7

7>6 所以接着往上冒泡

7>2 继续冒泡

至此达到了最大的数7，接下来还是从第一位开始寻找第二大的数。

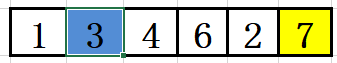
至此完成了第二个数的查找，我们知道冒泡算法的基本原理就是将最大的一点点浮到高的位置。每次仅挑选出来当前最大的数，6个数字循环五次就可以完全排序，因为最后两个数排序依次就可以变为有序。

这有一个动图（https://www.cnblogs.com/onepixel/articles/7674659.html）非常形象

算法分析：

1.需要两层循环第一层固定当前最大的位置，第二层用于遍历剩下的元素，将大的一点点浮上来。

2.需要一个临时变量，用于交换两个元素。

实际代码：(实际例子就使用java写了，比较通用的写法，其他程序也差不多，推荐的在线网站https://tool.lu/coderunner/)

class Untitled {
	public static void main(String[] args) {
		int[] array = new int[]{4,3,1,7,6,2};  //我们的需要排序的数组
		int temp=0;  //临时变量


         //循环次数 只需要数组长度-1次就可以 因为两个数的时候只需要排序一次
         //i变量用于定位 从数组的最后一位开始 存储当前最大的数
		for(int i=array.length-1;i>0;i--) 
		{

			for(int j=0;j<i;j++)  //内层遍历从0到该位置的所有元素
			{
				if(array[j]>array[j+1])  //大于就交换 否则不变
				{   
					temp = array[j+1];
					array[j+1]=array[j];
					array[j]=temp;
				}
			}
		}
		
        //输出显示排序后的  这种写法是java独有的 也可以正常遍历 或是使用数组转字符串方法
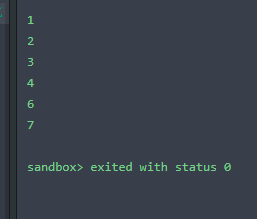
		for(int ele:array)
		{
				System.out.println(ele);
		}
	}
}