【Codeforces 1294D】MEX maximizing 题解（简单数学）

最新推荐文章于 2024-01-17 19:23:36 发布

原创最新推荐文章于 2024-01-17 19:23:36 发布 · 573 阅读

0 ·

CC 4.0 BY-SA版权

文章标签：

#算法 #数据结构

题解专栏收录该内容

11 篇文章

订阅专栏

本文介绍了一个关于MEX最大化的算法题解，通过分析和优化数组元素，利用模运算和数组记录技巧，实现MEX值的最大化，复杂度为O(n)。

MEX maximizing 题解（简单数学）

MEX maximizing

这个题是一个比较简单的题目稍作分析即可：
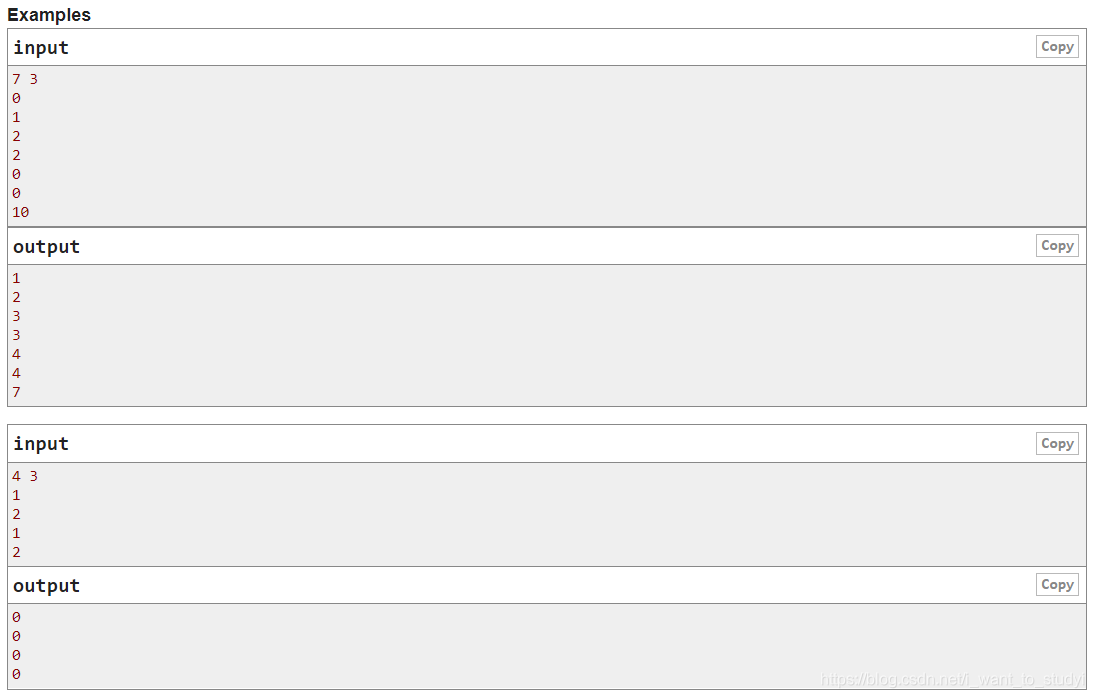
MEX maximizing题目描述

题意：
MEX：给出一个数组求出除去这个数组中的元素之外的最小的非负整数

此时在给定一个x 可以对数组中的任意一个元素加上或减去x（但是进行这个操作之后要保证这个元素仍然是一个非负整数）使得这个数组的MEX最大

思路：
这个题想一想也没什么巧妙的方法应该就是直接暴力
注意到MEX是最小的非负整数因此数组中的元素要将MEX“挤”上去的话应该要保证元素不重复的情况下尽可能的小

而因为每一个数都可以与x进行加减操作所以每一个数y都可以表示成：
y=k*x+t
那么对于输入的任意一个y而言都可以用模x的余项t来表示
那么这时就可以开一个数组来记录 t 对应的 k 的大小

然后再开一个数组记录已经有元素占有的位置
就可以开始搜索这个MEX了
复杂度O(n)

#详见代码#

#include<cstdio>
#include<cstring>
#include<algorithm>
using namespace std;
const int maxx=4e5+10;

int xnow[maxx],vis[maxx];
//  这个数组表示 当前这个的余项 到了几（因为输入的每一个数 都与x之间有一个余项）
//  输入的这个数 是什么类型  就只用看这个余项就可以了 
//  vis  就用来记录  有哪些数字是已经被占用了的 （因为 x最大也就maxx ）
//  （输入的数的个数最多也就maxx）  所以y  的数值不用很是在意 
int q,x,y,k,point,t;

int main(){
	scanf("%d%d",&q,&x);
	point=0;
	
	for(int ii=1;ii<=q;ii++){
		scanf("%d",&y);
		
		k=y%x;
		t=k+x*xnow[k];
		if(t<=maxx){
			vis[t]=1;
			xnow[k]++;
		}
		
		for(;point<=maxx;point++){
			if(vis[point]==0){
				break;
			}
		}
		
		printf("%d\n",point);
	} 
	
	return 0;
}