BARF阅读笔记----NeRF与Pose的联合优化

最新推荐文章于 2024-06-23 08:55:02 发布

原创

最新推荐文章于 2024-06-23 08:55:02 发布 · 1.2k 阅读

4 ·

CC 4.0 BY-SA版权

文章标签：

#人工智能 #计算机视觉

文章介绍了BARF方法，它将相机姿态细化与NeRF模型优化相结合，采用粗到细的策略提高训练稳定性。BARF解决了原始NeRF中位置编码导致的问题，并能处理不精确的相机位姿，对传统图像配准的理论进行了扩展，适用于3D多帧设置。此外，还提出了分阶段训练位置编码以增强模型拟合能力。

1. 前言

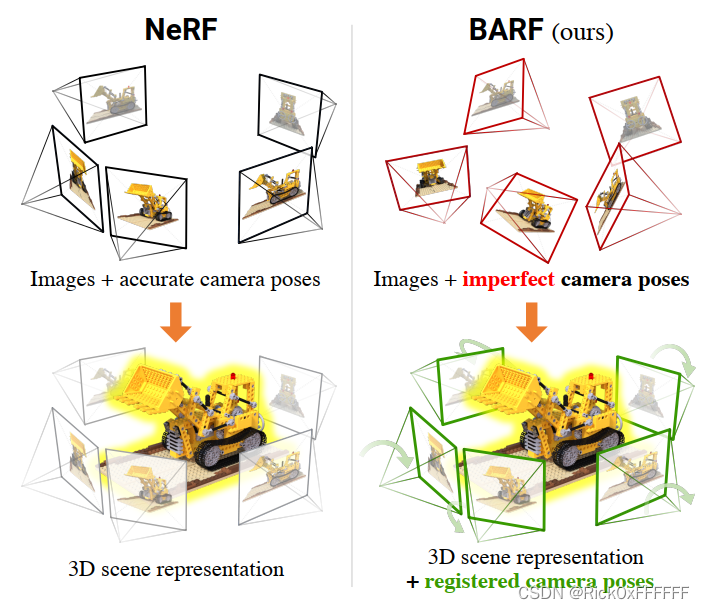
🤮Bundle-Adjustment Neural Radiance Fields提出了一个联合优化粗糙相机位姿与NeRF模型的新问题，并证明了适用于传统图像配准的coarse-to-fine方法也同样适用于NeRF。作者发现原有NeRF的naive position encoding方法会对图像合成产生不良影响。与上文从iNeRF开始学习Pose Refinement的区别是，BARF采用了联合优化的方式，将Pose Refinement这一问题又提升到了新的高度，相信对未来的offline pose estimation将会产生重大意义。
Alt

2. Contributions

从理论上耦合了pose refinement和 NeRF optimization问题。
提出了一种coarse-to-fine的策略来优化NeRF模型, 使训练更稳定。
BARF可以利用不准确的相机位姿对场景进行建模表达。

3. Method

3.1 Background

在2D图像中，经典的图像配准描述如下：已知两相邻帧 $\mathcal{I}_1$ 和 $\mathcal{I}_2$ ，要求解出两帧间的位姿变化问题可被形式化的表述为：

$\min_{\mathbf{p}}\sum_{\mathbf{x}}\Vert \mathcal{I} _1(\mathcal{W}(\mathbf{x};\mathbf{p}))-\mathcal{I}_2(\mathbf{x})\Vert^2_2$

用神经网络 $f:\mathbb{R}^2\rightarrow \mathbb{R}^3$ 来表示图像，上式被重塑为以下形式：
$\min_{\mathbf{p,\Theta}}\sum_{\mathbf{x}}( \Vert(f (\mathbf{x;\Theta} )-\mathcal{I}_1(x)\Vert^2_2+\\ \Vert(f (\mathcal{W}(\mathbf{x;p});\mathbf{\Theta} )-\mathcal{I}_2(x)\Vert^2_2 )$
或者简化为以下形式：
$\min_{\mathbf{p_1,p_2,\Theta}}\sum^M_{i=1}\sum_{\mathbf{x}}( \Vert(f (\mathcal{W}(\mathbf{x;p}_i);\mathbf{\Theta} )-\mathcal{I}_i(x)\Vert^2_2)$