C语言 - 位操作符例题

写一个函数返回参数二进制中 1 的个数。

例如 ：00000000101010101000110010101101  i从0到31循环，也就是每次循环都是这个二进制序列往右移动i位，即遍历二进制序列的每一位，再与1按位与，就可以得到最低位。 

 

k = k & k-1 就可以把最低位的1消去，消去n次就有n个1 

 

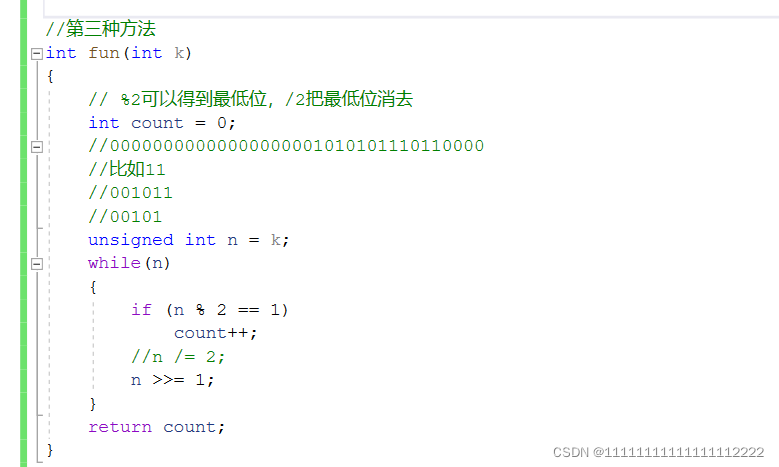
如同十进制数字%10/10一样，得到最低位，消去最低位，二进制数是%2/2，其实除2的效果相当于右移1，都是达到缩小一半的效果。注意改为无符号数，防止-1这样的数字影响计算，让内存中存储的补码的二进制位每一位都是有效的数字，才能达到效果。 

 

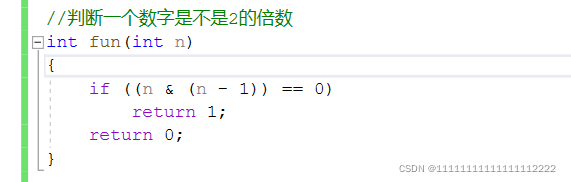
2的倍数的数字二进制序列中一定只有一个1，必须意识到这个才能进行下一步，消去最低位的1，如果消去之后为0，证明只有一个1。 

 

 

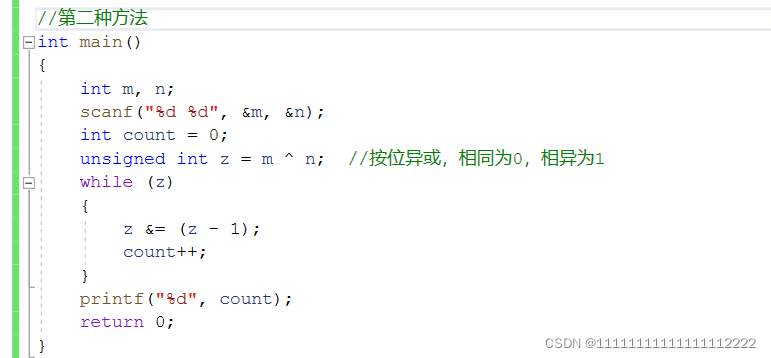
 这里定义unsigned int 和 int都可以，因为每次z&=z-1都可以达到消去最低位的1的效果。

比如-1，-1&-2：11111111111111111111111111111111 和 11111111111111111111111111111110相互按位与，结果就是11111111111111111111111111111110，也可以达到消去最低位的1的效果，只不过如果设定为unsigned int，则z中存储的原反补都是11111111111111111111111111111111。