数据结构（C）:二叉排序树的删除和调平

1.删除

虽然，二叉排序树的插入都在叶子节点，但是删除却可以分为三种不同的情况；
（1）删除的节点刚好是叶子结点——直接删除

(2)删除的节点只有左孩子或者只有右孩子，直接让其唯一的那个孩子去替代父母的位置
（如果24只有右孩子：不用担心24的右孩子会不会比24的父母还大，因为如果24右孩子比24父母（45）还大，那么在建树的时候就会放到45的右孩子上，所以，根的左子树上的所有节点都要比它小。）

（3）删除的节点既有左孩子又有右孩子，两种删除方法
①左子树“上位”，右子树合并到左子树，因为右子树上节点肯定都比左子树上的大，所以把右子树的根接到左子树的最右下角。
②左子树最右下角作为最接近被删节点的节点之一，可以直接替代子树的父母

以上的两种方法都可以作镜像变换，比如左子树最大对应右子树最小

调平（简单方法—>¹）

常规精简方法
因为二叉排序树有变成单只树（线性表）的风险，为了保证二叉排序树的效率与log2n同数量级,所以要将二叉排序树调成平衡二叉树。
平衡二叉树：根结点的左子树深度-右子树深度的绝对值不超过1。
不平衡共有以下四种情况
调平关键是：找到最小的非平衡二叉树的根其平衡因子绝对值一定是2，则其之前的平衡因子绝对值一定为1，分清除不平衡的类型
（1）最小的非平衡二叉树的根（A）的左子树(AL)的左子树上加了节点导致其不平衡简称（LL型）
做法：AL上去，A下来作为AL的右孩子，AL原本的右孩子作为A的左孩子

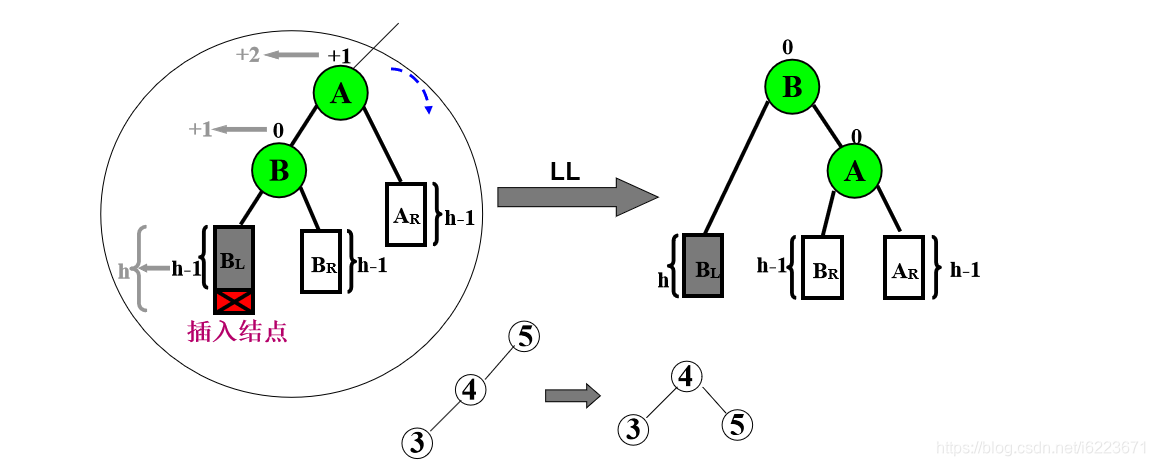
（2）RR型
做法：AR上去，A下来作为AR的左孩子，AR原本的左孩子作为A的右孩子

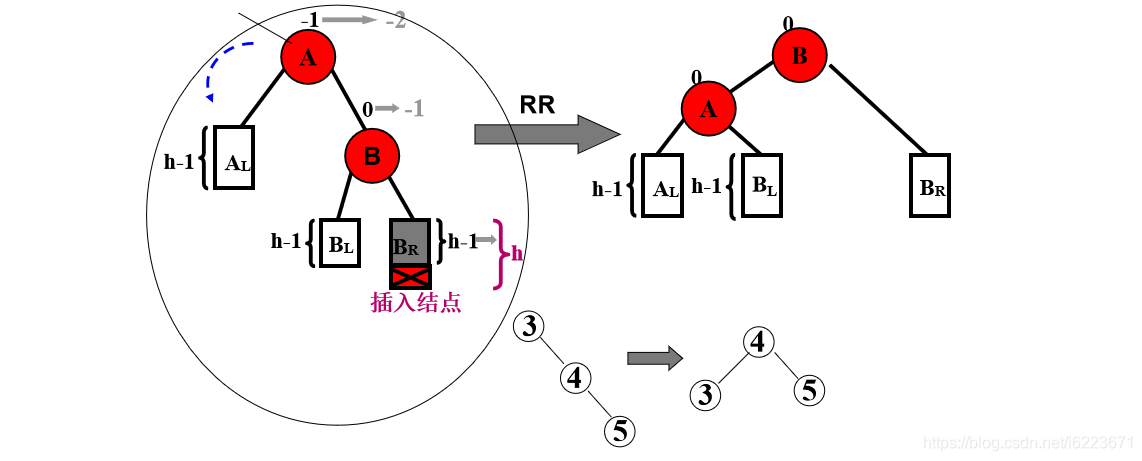
（3）LR型
①ALR（A的左孩子的右孩子）上去；②AL作为ALR的左孩子，ALR左孩子放到AL的右孩子；③A作为ALR的右孩子，ALR的右孩子放到A的左孩子。

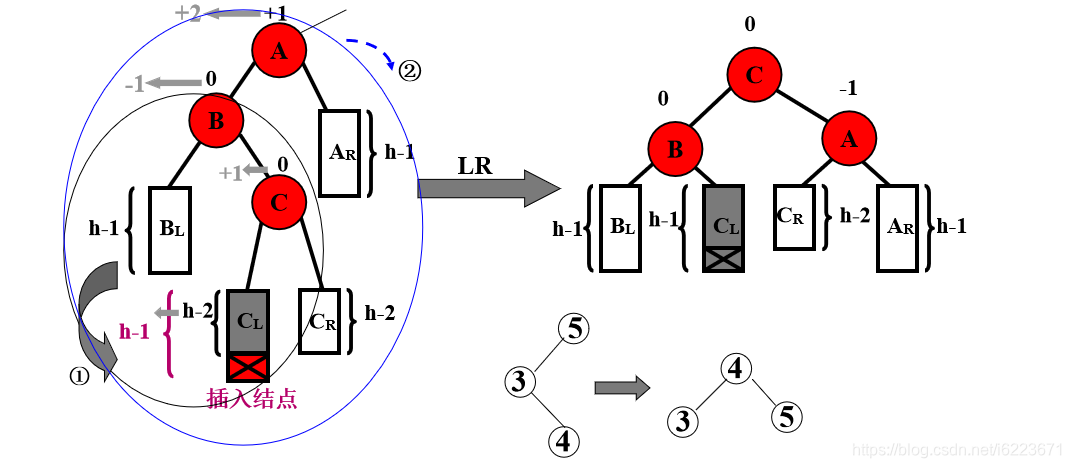
（4）RL型
①ARL（A的右孩子的右孩子）上去；②AR作为ALR的右孩子，ARL右孩子放到AR的右孩子；③A作为ARL的左孩子，ARL的左孩子放到A的右孩子。

---

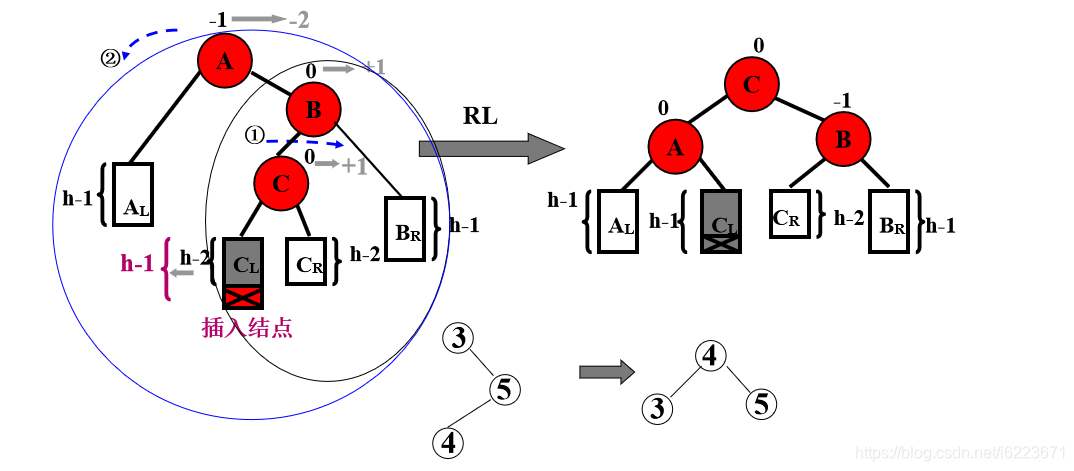
1. 调平的简单方法（不用死记硬背）
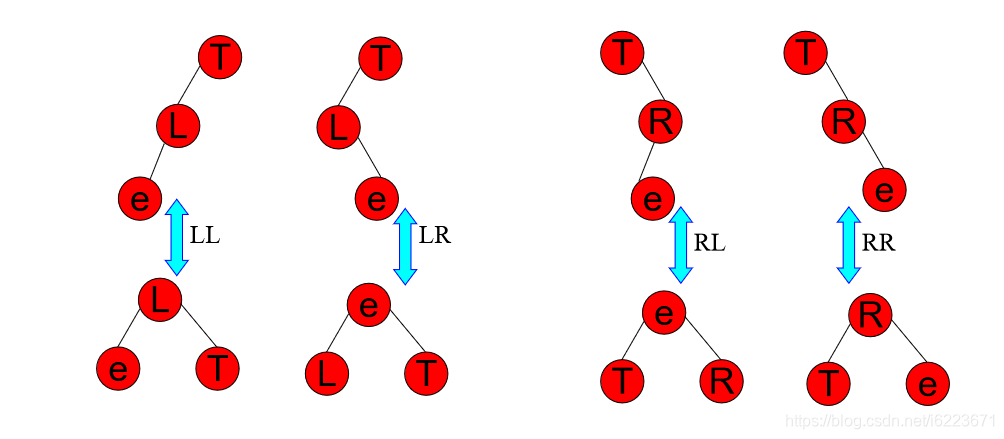
   将不平的最小树简化成下面的模型，其中位于中间的节点直接上升为根节点，其余两侧的节点随即成为它的左右孩子，原本中间节点的左右孩子，顺势挂在左右两边的节点上。（其中e可以表示为在空节点上插入，也可以表示成在非空节点上插）
   ↩︎