树的直径求解-优快云博客

本文链接：https://blog.youkuaiyun.com/hzk_cpp/article/details/86410026

一.树直径的定义.

树的直径：一棵树的直径定义为这棵树上一条边权和最大的路径.

显然一棵树可以有不止一条直径.

二.树直径的求解.

一般来说树的直径可以用树形DP来求.

设 $f [i] [0 / 1]$ 表示在 $i$ 的子树中以 $i$ 为一端的最长 $/$ 次长链长度，我们可以很容易DP出来这个值，树的直径就是 $f [i] [0] + f [i] [1]$ 的最大值.

同时我们还可以在DP的时候记录一下 $f [i] [0 / 1]$ 对应的从 $i$ 连向儿子的边，这样就可以求树的直径的方案了.

时间复杂度 $O (n)$ .

若不带方案的话，在DP的时候可以不用将次长链记录下来，直接在更新当前最长链之前用原来的最长链和现在的链拼接一下更新答案即可.

不带方案的版本如下：

int dp[N+9];

int Dfs_dp(int k,int fa){      //树形DP
  int res=0;
  for (int i=lin[k];i;i=e[i].next)
    if (e[i].y^fa){
      res=max(res,Dfs_dp(e[i].y,k));
      res=max(res,dp[k]+dp[e[i].y]+e[i].v);
      dp[k]=max(dp[k],dp[e[i].y]+e[i].v);
    }
  return res;
}

不过一旦带上方案，上面的做法就不行了，因为方案需要用到LCA次长链对应的儿子.

带方案的版本如下：

int dp[N+9][2],pre[N+9][2];

void Update(int k,int id){      //更新最长链和次长链
  int v=dp[e[id].y][0]+e[id].v;
  if (v>dp[k][0]){
  	dp[k][1]=dp[k][0];pre[k][1]=pre[k][0];
  	dp[k][0]=v;pre[k][0]=id;
  }else if (v>dp[k][1]) dp[k][1]=v,pre[k][1]=id;
}

int Dfs_dp(int k,int fa){      //树形DP
  int res=0;
  dp[k][0]=0;dp[k][1]=-INF;
  for (int i=lin[k];i;i=e[i].next)
    if (e[i].y^fa){
      res=max(res,Dfs_dp(e[i].y,k));
      Update(k,i);
    }
  return max(res,dp[k][0]+dp[k][1]);
}

int dia[N+9],v[N+9],cd;

int Get_dia(){      //树形DP后求方案dia，并求出方案中每个点向前面那个点连边的边权v
  int res=Dfs_dp(1,0),mx=1;
  for (int i=1;i<=n;++i)
    if (dp[i][0]+dp[i][1]>dp[mx][0]+dp[mx][1]) mx=i;
  int k=mx;
  for (;k;k=e[pre[k][0]].y) dia[++cd]=k,v[cd]=e[pre[k][0]].v;
  reverse(dia+1,dia+cd+1);
  reverse(v+1,v+cd+1);
  v[cd+1]=e[pre[mx][1]].v;
  for (k=e[pre[mx][1]].y;k;k=e[pre[k][0]].y) dia[++cd]=k,v[cd+1]=e[pre[k][0]].v;
  return res;
}

三.非负边权树上的直径求解.

注意接下来所有的结论都不一定适用于负边权树.

对于边权非负的树，我们还有另一种求解的方法.

具体来说，我们可以先从任意一个点开始，找到距离这个点最远的那个点；再从我们找到的点开始，在找到距离这个点最远的点.此时两个最远点为端点的路径就是这棵树的一条直径.

找最远点的过程可以用dfs或者bfs实现，时间复杂度 $O (n)$ .

带方案版本的代码如下：

queue<int>q;
int dis[N+9],pre[N+9],vis[N+9];

void Bfs_dis(int st){      //bfs出距离
  for (int i=1;i<=n;++i) pre[i]=vis[i]=0;
  dis[st]=0;vis[st]=1;q.push(st);
  for (;!q.empty();){
  	int t=q.front();q.pop();
  	for (int i=lin[t];i;i=e[i].next)
  	  if (!vis[e[i].y]){
  	  	dis[e[i].y]=dis[t]+e[i].v;
  	  	pre[e[i].y]=i;
  	  	vis[e[i].y]=1;
  	  	q.push(e[i].y);
  	  }
  }
}

int dia[N+9],v[N+9],cd;

int Get_dia(){      //bfs后求方案dia，并求出方案中每个点向前面那个点连边的边权v
  int res,mx=1;
  Bfs_dis(1);
  for (int i=1;i<=n;++i)
    if (dis[i]>dis[mx]) mx=i;
  Bfs_dis(mx);
  for (int i=1;i<=n;++i)
    if (dis[i]>dis[mx]) mx=i;
  res=dis[mx];
  for (int k=mx;k;k=e[pre[k]^1].y) dia[++cd]=k,v[cd+1]=e[pre[k]^1].v;
  return res;
}

正确性证明：
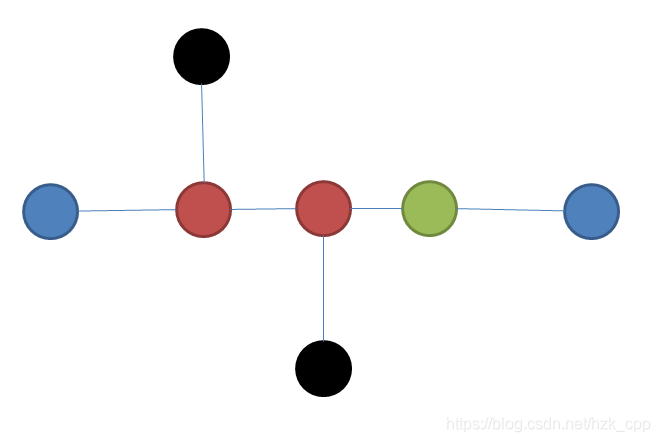
在这里插入图片描述
假设第一次从黑点出发找到最远点为蓝点，但存在一条路径端点为两个红点更长，且蓝点到黑点路径上有绿点与红点到红点路径上的某个橙点相连（可以是同一个点）.
那么此时两个红点到绿点的距离均没有蓝点到绿点的距离大，那么此时一个红点到蓝点的距离必然比它到另一个红点的距离大，与条件矛盾，原命题得证.
证毕.

通过这个证明过程我们也得到了一个非负边权树上直径的性质.

性质1：对于树上任意一个点出发的最长链，其另外一个端点必然是某条直径的端点.

四.非负边权树上直径交的性质.

性质2：对于一棵边权非负的树，这棵树的所有直径必然交于一点.

证明：
在这里插入图片描述
假设我们已经证明了某些直径交于蓝点，现在有一条两端为黑点的直径，且这条直径上有一个绿点与蓝点相连，并且有经过蓝点的某条直径为红点.
此时必然有某个红点到蓝点的距离与某个黑点到绿点的距离大于等于直径长度的一半，那么这个红点与这个黑点之间的距离就会大于直径长度，与条件矛盾，原命题得证.
证毕.

这个性质可以用来求所有直径的交，具体可以参考BZOJ3124 直径题解.

性质3：一条直径的中点（可能在边上）必然在其它直径上出现，且这个中点也是其它直径的中点.

证明：
在这里插入图片描述
假设有一条两端为蓝点的直径且中点为绿点，并有一条两端为黑点的直径与两端为蓝点的直径的交的两端为红点.
此时右边红点到右边蓝点的距离必定大于直径长度的一半，且上面黑点到右边红点的距离和下面黑点到右边红点的距离中必定也有一个大于直径长度的一半，加起来大于直径长度，与直径定义矛盾，原命题得证.
证毕.

五.一些非负边权树上的其它性质.