PAT顶级_2024秋(正赛35+模拟AK)-优快云博客

本文链接：https://blog.youkuaiyun.com/hzj913313180/article/details/142072165

长时间没复习英语，结果俩大模拟都意会错了意思，后面两个半小时里没搓出一个题，35分太捞了。回家想明白后买了模拟卷，都过了。
ps : 不能顶复试机考成绩后，PAT凉了一大截。这次顶级交过卷的只有12个，第一名65分，且无一人尝试解答所有题目（即选择第三题的就没时间想第二题(30 - x)，选择第二题的就没时间想第三题(30 x -)）

第一题

思路：

将所有操作记录在ops数组中，将所有查询、插入的数字记录在rec中，排序去重。
数组rec中的数字散列在 $[- 1 E 9, 1 E 9]$ ，而数字总可能性在 $3\times 10^5$ ，所以进行映射，以方便后续树状数组操作。
然后遍历ops数组：
- 对于Insert操作，在树状数组中相应下标位置＋1，表示这个数字出现过一次。
- 对于Query操作，查找到最小的满足sum(L) == sum(x - 1)的整数L，查找到最小的满足sum® > sum(x)的R，映射回去就是输出的区间。
- 边界处理不赘述。

#include<bits/stdc++.h>
using namespace std;
#define pii pair<int, int>
#define x first
#define y second
const int N = 300010, inf = 0x3f3f3f3f;
int tr[N]; 
int lowbit(int x){
	return x & -x;
}
void add(int x, int c){
	for(int i = x; i < N; i += lowbit(i))
		tr[i] += c;
}
int sum(int x){
	int res = 0;
	for(int i = x; i; i -= lowbit(i))
		res += tr[i];
	return res; 
}
int main(){
	char op;
	int x;
	vector<pii> ops;
	vector<int> rec;
	unordered_map<int, int> mp;
	unordered_map<int, int> rev;
	int idx = 1; // 树状数组必须从下标1开始 
	rec.push_back(-inf), rec.push_back(inf); 
	while(scanf("%c", &op), op != 'E'){
		scanf("%d", &x);
		getchar(); // !!
		rec.push_back(x);
		if(op == 'I'){
			ops.push_back({0, x});
		}else{
			ops.push_back({1, x});
		}
	} 
	sort(rec.begin(), rec.end());
	rec.erase(unique(rec.begin(), rec.end()), rec.end());
	
	for(auto& item : rec){
		mp[item] = idx;
		rev[idx ++] = item;
	}
		
	int ansl = 0, ansr = 0, redix = 0;
	for(auto& item : ops){
		if(item.x == 0){
			add(mp[item.y], 1);
		}else{
			redix = sum(mp[item.y] - 1); // 最小的和item.y - 1一样的; 
			int l = 1, r = mp[item.y] - 1;
			while(l < r){
				int m = l + r >> 1;
				if(sum(m) == redix) r = m;
				else l = m + 1;
			}
			ansl = l;
			redix = sum(mp[item.y]); // 最小的大于item.y的
			l = mp[item.y] + 1, r = idx - 1;
			while(l < r){
				int m = l + r >> 1;
				if(sum(m) == redix) l = m + 1;
				else r = m;
			} 
			ansr = r;
			printf("(");
			if(ansl == 1) printf("-inf, ");
			else printf("%d, ", rev[ansl]);
			if(ansr == idx - 1) printf("+inf)\n");
			else printf("%d)\n", rev[ansr]);
		}
	}
	return 0;
}

第二题

思路：

按着英文要求的一步步慢慢写就好

#include<bits/stdc++.h>
using namespace std;
#define pii pair<int, int>
#define x first
#define y second
const int N = 110, inf = 0x3f3f3f3f;
int n, ans1, ans2;
pii pos, ed;
int get_id(int x, int y){
	return x * n + y;
}
pii get_pos(int id){
	return {id / n, id % n};
}
int g[N][N];
int fire[N][N];
bool st[N][N];
int dest[N][N];
int lenrec[N][N];
int dx[5] = {0, -1, 1, 0, 0}, dy[5] = {0, 0, 0, -1, 1}; // 上、下、左、右 
unordered_map<int, int> mp; 
bool succeed = false;
bool check(int id, int from){
	// 从from来的火焰检测，看看a、b的妖怪是不是喷向from
	if(mp[id] == 1 && from == 2) return true;
	if(mp[id] == 2 && from == 1) return true;
	if(mp[id] == 3 && from == 4) return true;
	if(mp[id] == 4 && from == 3) return true;
	return false;  
}
priority_queue<pii, vector<pii>, greater<pii>> new_gra(vector<pii> yaos){
	memset(st, false, sizeof st);
	memset(fire, false, sizeof fire);
	set<int> protect;
	for(auto yao : yaos){
		auto yao_pos = get_pos(yao.x);
		int x = yao_pos.x, y = yao_pos.y;
		fire[x][y] = 2; // 妖怪，走不了 
	}
	
	for(auto yao : yaos){
		auto yao_pos = get_pos(yao.x);
		int x = yao_pos.x, y = yao_pos.y;
		int forward = yao.y;
		while(true){
			x += dx[forward], y += dy[forward];
			if(x >= n || y >= n || x < 0 || y < 0) break;
			if(fire[x][y] == 2){
				protect.insert(get_id(x, y));
				break;
			}
			fire[x][y] = 1;
		}
	}

	// 计算dest 
	memset(st, false, sizeof st);
	memset(dest, 0x3f, sizeof dest);
	st[pos.x][pos.y] = true; dest[pos.x][pos.y] = 0;
	queue<pii> q; q.push({pos.x, pos.y});
	while(q.size()){
		auto tar = q.front(); q.pop();
		st[tar.x][tar.y] = false;
		for(int i = 1; i <= 4; i ++){
			int x = tar.x + dx[i], y = tar.y + dy[i];
			if(x >= n || y >= n || x < 0 || y < 0) continue; 
			if(fire[x][y] == 2) continue;
			if(dest[tar.x][tar.y] + 1 < dest[x][y]){
				dest[x][y] = dest[tar.x][tar.y] + 1;
				if(!st[x][y]){
					st[x][y] = true;
					q.push({x, y}); // SPFA;
				}
			}
		}
	}	


	priority_queue<pii, vector<pii>, greater<pii>> killcost;
	if(dest[ed.x][ed.y] == inf) return killcost; 
	int ptrx = ed.x, ptry = ed.y;  // 指针记录路径 
	int tmpi[5] = {0, 1, 3, 4, 2}; 
	set<pii> firefrom;
	succeed = true;
	if(fire[ed.x][ed.y]) succeed = false;
	while(ptrx != pos.x || ptry != pos.y){
		for(int i = 1; i <= 4; i ++){
			int x = ptrx + dx[tmpi[i]], y = ptry + dy[tmpi[i]];
			if(x >= n || y >= n || x < 0 || y < 0) continue;
			if(dest[x][y] != dest[ptrx][ptry] - 1) continue; 
			ptrx = x, ptry = y;
			if(fire[x][y] == 1){ // 记录喷火来源到firefrom
				succeed = false;
				for(int j = 1; j <= 4; j ++){
					int a = ptrx + dx[j], b = ptry + dy[j];
					if(a >= n || b >= n || a < 0 || b < 0) continue;
					if(fire[a][b] == 0) continue; // 这方向没有火
					if(fire[a][b] == 2){ // 查找这个妖怪的方向是不是 
						if(check(get_id(a, b), j))
							firefrom.insert({a, b});
						continue;
					}
					while(fire[a][b] == 1){
						a += dx[j], b += dy[j];
						if(a >= n || b >= n || a < 0 || b < 0) continue;
						if(fire[a][b] == 2){
							firefrom.insert({a, b});
							break;
						}
					}
				} 
			}
			
			break; // 就朝着一个方向前进 
		}
		//cout << endl;
	}

	
	memset(lenrec, 0x3f, sizeof lenrec);
	memset(st, false, sizeof st);
	lenrec[pos.x][pos.y] = 0, st[pos.x][pos.y] = true;
	while(q.size()) q.pop();
	q.push({pos.x, pos.y});
	while(q.size()){
		auto tar = q.front(); q.pop();
		for(int i = 1; i <= 4; i ++){
			int x = tar.x + dx[i], y = tar.y + dy[i];
			if(x >= n || y >= n || x < 0 || y < 0 || st[x][y]) continue; 
			if(fire[x][y] == 1) continue; // 走不通
			if(fire[x][y] == 2){
				if(protect.count(get_id(x, y))) continue; // 妖怪杀不了 
				if(firefrom.count({x, y})){
					killcost.push({lenrec[tar.x][tar.y] + 1, get_id(x, y)}); 
				}
					
				continue;
			} 
			lenrec[x][y] = min(lenrec[x][y], lenrec[tar.x][tar.y] + 1);
			st[x][y] = true;
			q.push({x, y});
		}
	}
	
	return killcost;		

}
int main(){
	cin >> n;
	vector<pii> yaos;
	for(int i = 0; i < n; i ++){
		for(int j = 0; j < n; j ++){
			cin >> g[i][j];
			if(g[i][j] == 5) pos = {i, j};
			else if(g[i][j] == 6) ed = {i, j};
			else if(g[i][j]){
				yaos.push_back({get_id(i, j), g[i][j]});
				mp[get_id(i, j)] = g[i][j];
			}
		}
	}
	while(true){
		auto killcost = new_gra(yaos);
		if(killcost.empty()){
			// 可能成功、失败 
			if(succeed){
				cout << ans1 + dest[ed.x][ed.y] << ' ' << get_id(ed.x, ed.y) + 1 << endl;
				cout << "Win";
			}else{
				cout << ans1 << ' ' << get_id(pos.x, pos.y) + 1 << endl;
				cout << "Lose";
			}
			return 0;
			
		}else{
			auto tar_yao = killcost.top();
			vector<pii> new_yaos;
			for(auto yao : yaos){
				if(yao.x == tar_yao.y) continue;
				new_yaos.push_back(yao);
			}
			yaos = new_yaos;
			pos = get_pos(tar_yao.y);
			ans1 += tar_yao.x;
		} 
	} 
	
	return 0;
}

第三题

思路：

按着英文要求的一步步慢慢写就好。
注意代码可能存在不规范，比如第一行末尾是ma，第二行开头是in。
注意每次找到重复的长度超过阈值的字段是单独一行输出，而不是拼接整体输出，这点没理解就只能有5分。
注意DP别想复杂了，下面这个DP求法的正确性其实很容易证明。

#include<bits/stdc++.h>
using namespace std;
const int N = 1010; // total len < 1010
string name1, name2;
string str1 = "", str2 = "";
int L, T;
string ansL;
int dp[N][N];
bool check(char c){
	if(c >= 'a' && c <= 'z') return true;
	if(c >= 'A' && c <= 'Z') return true;
	if(c >= '0' && c <= '9') return true;
	return false;
}
unordered_set<string> delkey = {"main", "return", "if", "else", "for", "do", "while", "int", "float", "double"};
int main(){
	cin >> T >> name1;
	string str, strtmp = "";
	getchar();
	while(getline(cin, str), str != "$"){
		string sub = "", strtmpline = "";
		str = str + " ";
		for(auto& c : str){
			if(check(c)){
				sub += c;
			}else{
				// 得到了一个字符，检查
				if(delkey.count(sub)){
					strtmpline += sub + c;
					sub = "";
					continue;
				} else{
					if(sub.size()) strtmpline += 'x';
					sub = "";
					strtmpline += c;
				}
				
			}
		}
		strtmp += strtmpline;
	}
	for(auto& c : strtmp){
		if(c == ' ' || c == '\n'){
			continue;
		}
		str1 += c;
	}
	cin >> name2;
	strtmp = "";
	getchar();
	while(getline(cin, str), str != "$"){
		str = str + " ";
		string sub = "", strtmpline = "";
		for(auto& c : str){
			if(check(c)){
				sub += c;
			}else{
				// 得到了一个字符，检查
				if(delkey.count(sub)){
					strtmpline += sub + c;
					sub = "";
					continue;
				} else{
					if(sub.size()) strtmpline += 'x';
					sub = "";
					strtmpline += c;
				}
			}
		}
		strtmp += strtmpline;
	}
	for(auto& c : strtmp){
		if(c == ' ' || c == '\n'){
			continue;
		}
		str2 += c;
	}	
	//cout << str1 << endl << str2 << endl;
	int L1 = str1.size(), L2 = str2.size();
	// find same;
	string substr1 = "", substr2 = "", substrcom = "";
	str1 = " " + str1, str2 = " " + str2;
	while(true){
		memset(dp, 0, sizeof dp);
		
		
		for(int j = 1; j < str2.size(); j ++){
			for(int i = 1; i < str1.size(); i ++){
				dp[i][j] = max(dp[i][j - 1], dp[i - 1][j]);
				if(str1[i] == str2[j]){
					dp[i][j] = max(dp[i][j], dp[i - 1][j - 1] + 1);
				}
			}	
		}		
		int ptri = str1.size() - 1, ptrj = str2.size() - 1; 
		while(ptri && ptrj){
			if(dp[ptri][ptrj] == dp[ptri - 1][ptrj]){
				substr1 = str1[ptri --] + substr1;
			}else if(dp[ptri][ptrj] == dp[ptri][ptrj - 1]){
				substr2 = str2[ptrj --] + substr2;
			}else if(str1[ptri] == str2[ptrj] && dp[ptri][ptrj] == dp[ptri - 1][ptrj - 1] + 1){
				substrcom = str1[ptri] + substrcom;
				ptri --, ptrj --;
			}
		}
		while(ptrj){
			substr2 = str2[ptrj --] + substr2;
		}
		while(ptri){
			substr1 = str1[ptri --] + substr1;
		}
		
		
		if(substrcom.size() > T){
			L += substrcom.size();
			cout << substrcom << endl; 
			str1 = " " + substr1, str2 = " " + substr2, substrcom = "";
			substr1 = "", substr2 = "";
		}else{
			break;
		}
	}
	cout << name1 << ' ' << name2 << ' ';
	printf("%.2f", max((double)L / L1, (double)L / L2));
	return 0;
}

T-1 The Smallest Open Interval

Given a set S of points on the x-axis. For any point p, you are suppose to find the smallest open interval that contains p, provided that the two ends of the interval must be in S.

Input Specification:

Each input file contains one test case. Each case consists of several lines of commands, where each command is given in the format:

cmd num

where cmd is either I for “insert”, or Q for “query”, or E for “end”; and num is an integer coordinate of a point on the x-axis. It is guaranteed that num is in the range [−109,109].
The input is ended by E. It is guaranteed that there are no more than 105 distinct points in S, and so is the number of queries. The total number of commands (E not included) is no more than 3×105.

Output Specification:

For each I case, insert num into S. For each Q case, output the smallest open interval that contains num in the format (s1, s2), where both s1 and s2 must be in S. On the other hand, if num is no larger than the smallest point in S, s1 shall be replaced by -inf, representing negative infinity; or if num is no smaller than the largest point in S, s2 shall be replaced by +inf, representing positive infinity.
It is guaranteed that there must be at least 1 point in S before the first query.

Sample Input:

I 100
Q 100
I 0
I 33
I -200
Q 25
Q 33
Q -200
Q 200
E

Sample Output:

(-inf, +inf)
(0, 33)
(0, 100)
(-inf, 0)
(100, +inf)

T-2 Breaking Through

In a war game, you are given a map consists of n×n square blocks. Starting from your current block, your task is to conquer a destination block as fast as you can. The difficulties are not only that some of the blocks are occupied by enemies, but also that they are shooting in some directions. When one is shooting in some direction, the whole row/column in that direction will be covered by fire, unless there is another enemy blocking the way. You must make sure that you are not shot on the way to your destination.

However, it is very much likely, at the very beginning, that this task is impossible. So you must follow the following instructions:

Step 1: find the shortest path from the starting block to the destination, avoiding all the enemy blocks. The path length is the number of blocks on the way, not including the starting block.
If this path is not unique, select the smallest index sequence – that is, all the blocks are indexed from 1 to n2, starting from the upper-left corner, and row by row till the lower-right corner. An index sequence is an ordered sequence of the block indices from the starting block to the destination. One sequence { s,u1,⋯,uk,d } is said to be smaller than { s,v1,⋯,vk,d }, if there exists 1≤p≤k such that ui=vi for i<p and up<vp.
Step 2: if some of the blocks along the selected shortest path is covered by fire, conquer and clear the nearest reachable enemy block that are firing at the path (in case that such a block is not unique, take the one with the smallest index). Then take that block as the starting position, goto step 1. Keep in mind that you must always make sure that you are not shot on the way.
If step 2 is impossible, then the game is over. Otherwise, keep going until you finally conquer the destination.

Input Specification:

Each input file contains one test case. For each case, the first line contains a positive integer n (3≤n≤100), which is the size of the map. Then n lines follow, each gives n numbers. Each number describes the status of the corresponding block:

0 means the block is clear;
1, 2, 3, or 4 means the block is occupied by an enemy, who will shoot toward up, down, left, and right, respectively;
5 means the block is your starting position;
6 means the block is your destination.
All the numbers in a line are separated by a space.

Note:

You can never cross any of the boundaries of the map.
When an enemy is shooting from block A in direction B, every block starting from A in direction B will be covered by fire, untill the boundary is reached, or another enemy block is encountered.
The enemies will never kill each other. Only you will get killed if you step into a block that is covered by fire.
It is guaranteed that there is no more than n enemy blocks, and your starting position is not on fire.

Output Specification:

Print in a line the path length for you to reach the last block from your starting position, and the block number. The two numbers must be separated by 1 space.
In the next line, print Win if the destination is reached, or Lose if not.

Sample Input 1:

6
6 2 0 0 0 0
0 0 0 0 0 0
0 4 0 0 0 0
0 0 0 0 1 0
0 0 0 3 5 0
4 0 0 0 0 0

Sample Output 1:

10 1
Win

Hint:

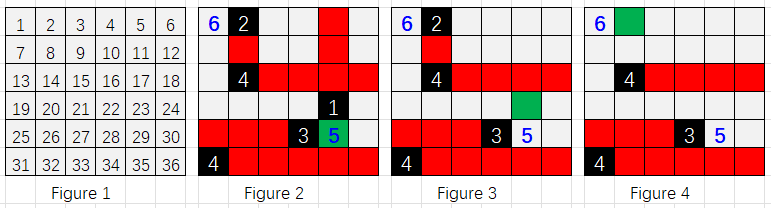
The movements are shown by the following figures 1~4.
Figure 1 shows how the blocks are numbered.
Figure 2 shows the initial status of the map, where the player’s position is green, enemy blocks are black, and red blocks are covered by fire.
At the very beginning the shortest path was 29->30->24->18->12->11->10->9->8->7->1, but the path was covered by fire shooting from blocks 23, 14 and 2. Since the enemy block 23 is the nearest reachable one, it was cleared with path length 1.
Now starting from block 23, the shortest path was 23->17->11->10->9->8->7->1, but the path was covered by fire shooting from blocks 14 and 2. Since the enemy block 14 is covered by fire from block 2, taking block 2 now is the only option. So next, block 2 is cleared with path length 8 (crossing the destination).
Finally we can get to the destination from block 2 to 1.

Sample Input 2:

Sample Output 2:

6 3
Lose

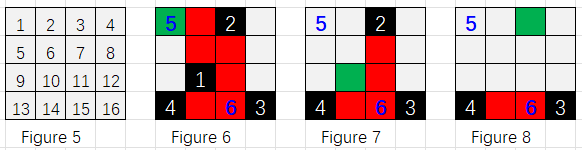
Hint:

The movements are shown by the following figures 5~8.
Figure 5 shows how the blocks are numbered.
Figure 6 shows the initial status of the map.
At the very beginning the shortest path was 1->2->6->7->11->15, but the path was covered by fire shooting from blocks 3, 10, 13 and 16. Since the enemy block 10 is the nearest reachable one, it was cleared with path length 3.
Now starting from block 10, the shortest path was 10->11->15, but the path was covered by fire shooting from blocks 3, 13 and 16. Since the enemy blocks 13 and 16 are covered by fire from each other, taking block 3 now is the only option. So next, block 3 is cleared with path length 3.
Now it is clear that there is no way to conquer the destination, since block 15 is fired by 13 and 16, yet we cannot clear any of them without getting fired. Hence the last block we can reach is 3.

T-3 Code Plagiarism Detection

Your job is to implement a simple version of the Code Plagiarism Detection algorithm. The algorithm works in the following way:

Step 1: Get tokens. A “token” is defined to be a continuous, uninterrupted substring of letters and numbers in a code.
Step 2: Get keywords. Here we only take the keyword set S={ main, return, if, else, for, do, while, int, float, double } into consideration, and replace every other token by x.
Step 3: Delete white-space characters and comments – it would be quite complicated to remove the comment lines. Here we simplify it as to just remove the space and the return.
Step 4: Let’s denote the two code strings which have been processed by the previous 3 steps as C1 and C2, with the lengths L1 and L2, respectively. Initialize the length of the duplicated code to be L=0. Let LT be the threshold（阈值）of the duplicated code length. Repeat the following steps:
(4.1) Find the longest common subsequence of C1 and C2 and record its length len. If len>LT, goto (4.2); else goto (4.3).
(4.2) Delete the longest common subsequence from C1 and C2. Increment L by len. Goto (4.1) for updated C1 and C2.
(4.3) Calculate the code similarity, which is defined to be max(L/L1,L/L2).

Note:

1. A subsequence of a given sequence X={x1,x2,⋯,xn} is obtained by removing several elements from X. For example, given X={ H, E, L, L, O }, sequences like { E, L, O }, { H, O } and { L } are all its subsequences.
1. If the longest common subsequence is not unique, we must first match the left-most possible character of C1. In case that one character of C1 can match several characters of C2, we must first match the left-most possible character of C2. Hence the result will be unique.

Input Specification:

Each input file contains one test case. For each case, the first line gives a non-negative integer LT (≤10). Then two pieces of code are given in the following format:

The first line contains the file name of the code, which is a string of no more than 20 letters and numbers.
Then several lines of code are given, and is ended by $ together with a return.

It is guaranteed that $ is not part of the code.
It is guaranteed that the original code consists of no more than 103 characters, and it will not be empty after the first 3 steps of processing.

Output Specification:

Output in a line the duplicated codes detected during each iteration.
In the last line, print the 1st and the 2nd file names, and the code similarity (output 2 decimal places).
All the strings/numers in a line must be separated by 1 space, and there must be no extra space at the beginning or the end of the line.

Sample Input:

5
file1
#include<stdio.h>
int main()
{ int tmp=100;
  printf("hello world");
  while(tmp) tmp--;
  return 0;
}
$
file2
#include<stdio.h>
void main()
{
    int i=10;
    while(i) i--;
    cout<<"hello world"<<endl;
}
$

Sample Output:

#x<x.x>main(){intx=x;while(x)x--;x;}
file1 file2 0.78

Hint:

The first file name is file1. After the first 3 steps, the code C1 is:

#x<x.x>intmain(){intx=x;x("xx");while(x)x--;returnx;}

The second file name is file2. After the first 3 steps, the code C2 is:

#x<x.x>xmain(){intx=x;while(x)x--;x<<"xx"<<x;}

After the pre-process, the length of file1 is 53, and that of file2 is 46. After the first run, the following duplicated code of length 36 is detected:

#x<x.x>main(){intx=x;while(x)x--;x;}

Then deleting the duplicated pieces, C1 and C2 are updated as:

intx("xx");return
x<<"xx"<<x

Repeat and obtain in the second run:

x"xx"

Since the above code length is 5, not exceeding the thrshold 5, it is not counted.
Hence the final result is 36 with similarity max(36/53,36/46)=0.78.