神经网络的反向传播公式推导

写在前面

机器学习算法工程师的面试中常会问到一个很基础的问题，那就是反向传播公式的推导，今天看了下吴恩达老师的公开课《神经网络和深度学习》，将一些推导过程记录下来。

逻辑回归反向传播的推导

逻辑回归是最简单的神经网络，先从逻辑回归入手，有助于后面的理解。

上图是一个逻辑回归正向传播的示意图。具体细节不再描述。

损失函数$L(a, y) = -yloga-(1-y)log(1-a)$，反向传播的目的是为了求 $\mathrm{d}w$ 和 $\mathrm{d}b$，从而采用梯度下降法进行迭代优化。反向传播就是从后向前一步步求微分，从而得到$dw$ 和 $db$。具体过程如下：

(1) $\mathrm{d}a = \dfrac{\mathrm{d}L(a,y)}{\mathrm{d}a}= -\dfrac{y}{a} +\dfrac{1-y}{1-a}$
(2) $\mathrm{d}z = \mathrm{d}a \cdot g'(z)$
(3) $\mathrm{d}w=dz \cdot x$
(4) $\mathrm{d}b=dz$

这样就完成了逻辑回归的反向传播。

单隐层神经网络的反向传播推导

神经网络计算中，与逻辑回归十分相似，但中间会有多层计算。下图是一个双层神经网络，有一个输入层，一个隐藏层和一个输出层。

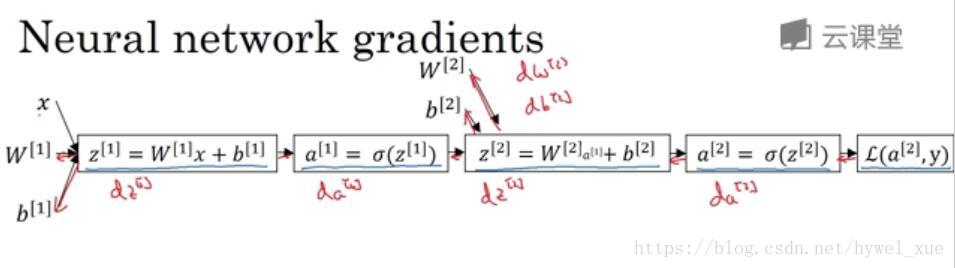
前向传播过程如图所示。其中L(a<