机器学习入门笔记-简易版线性回归算法理解加实例(最小二乘法)

线性回归算法

回归算法就是将一些连续的有一定规律的点拟合成一条直线或者曲线的形式，通过这条直线或曲线，就可以预测后来的点大致位置了。
比如说我们现在有八个散列的点，我用8×2的矩阵表示
x = np.array([
[0.5, 1],
[1, 1.8],
[1.5, 2.2],
[2, 2.3],
[2.5, 3],
[2.7, 3.1],
[2.9, 3.1],
[3.1, 3.3],
])
第一列代表二维空间中的x的值第二列代表y值，可以看到它们的分布是这样的：我们发现，这些点的分布大致都是朝着一个方向在递增的，这些点与点之前呢貌似存在着某一种线性的关系，假如能找到一条线能好好的拟合这些点的话，我们是不是就可以通过这条线来预测下一个点的位置。没错，我们的回归算法就是去干这个事情的，找到一条能较好拟合这些点的一条线，通过这条线来预测之后的走势与具体的值。

值得注意的是，我们之前一起探讨的knn算法是根据散列点来预测某个事物的类别是什么，而线性回归算法我们是用来预测某个具体的值，这也是他们之间的区别之一

咱们一起探讨了它的大致思路，但是怎样找到这一条线呢，一条哦。我们先用肉眼来测量测量
我在这里画了三条线，这三条其实都可以来模拟这些点的走向，你说这三条线之间的偏差，貌似也不大，那我们选择哪一条呢？当然是准确率或者说拟合程度最高的那一条，如何找到那一条线，就可以用到我们的最小二乘法了。
首先既然是条直线，我们可以假设这条直线的公式为y=ax+b，其中x和y的值我们都知道了就是之前那个叫x的8×2的矩阵，现在就是想办法吧未知的斜率a和截距b求出来了。这里我给出最小二乘法求a和b的公式：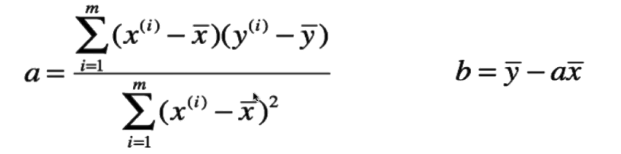
其中xi就是x1,x2,x3到xm，按照我上面给的坐标矩阵就是 [0.5, 1, 1.5, 2, 2.5, 2.7, 2.9, 3.1]
yi同理就是 [1, 1.8, 2.2, 2.3, 3, 3.1, 3.1, 3.3]
x头上戴横线叫x bar也就是这些x求平均数，也就是x1加到xm在除以m
y头上戴横线叫y bar也就是这些y求平均数，同理就是y1加到ym在除以m
好了我们求一求a和b,再把这条直线显示出来
有了这条线，那么这个时候你问我如果再来个x等于3.9，那么按照这些点分布的规律，他对应的y值是多少呢？
直接把x带进去就可求出y了：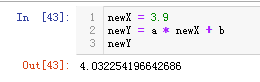

实际上拟合的线不一定是直线还有可能是曲线，这个例子较为简单一些，所以用直线就可以拟合，而且特征值可能也会比这个例子多得多。
注意哦，是想办法拟合不是重合，想办法重合这些点的话看似能较好的代表这些点的线性分布，但是这样会过分得依赖单个样本的数据，一个样本就可以对整个拟合的线产生巨大的影响，就预测来讲，这是不好的。

好了再来个例子运用一下

上面说了回归算法的大致思想，这次我们用这个算法来预测一下小明的成绩，小明第一次考试考了23分，觉得很羞耻于是决定发奋图强好好学习，事实上，通过努力小明之后很有进步，成绩确实提高了不少，每次考试的分数都比上一次高一些，我们来看下具体是多少。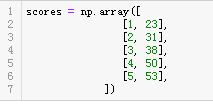
第一次考了23分，第二次考了31分，第三次38分···
现在要我们预测一下第六次他能不能及格(60分及格)，具体又是多少分呢？
看了下这些分数的大致走势差不多也是条直线吧，有了前面的思路，老规矩，使用最小二乘分求出求出这条直线的a和b，得到这条直线：
来预测预测第六次的吧：

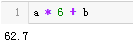
结果显示是62.7分，能及格。具体代码如下：

import numpy as np

class MyRegression:

    def __init__(self, train_x, train_y):
        self.train_x = train_x
        self.train_y = train_y

    def predict(self, p):
        x_mean = np.mean(self.train_x)
        y_mean = np.mean(self.train_y)
        a = np.dot((self.train_x - x_mean), (self.train_y - y_mean)) / np.dot((self.train_x - x_mean),(self.train_x - x_mean))
        b = y_mean - a * x_mean
        return a * p + b


if __name__ == '__main__':
    scores = np.array([
        [1, 23],
        [2, 31],
        [3, 38],
        [4, 50],
        [5, 53],
    ])
    mr = MyRegression(scores[:,0], scores[:,1])
    ps = mr.predict(6)
    print(ps)