一、 欧氏距离( Euclidean distance)
一个通常采用的距离定义,它是在m维空间中两个点之间的真实距离。在二维和三维空间中的欧式距离的就是两点之间的距离,
二维空间的公式
三维空间的公式
n维空间的公式
马氏距离是由印度统计学家马哈拉诺比斯(P. C. Mahalanobis)提出的,表示数据的协方差距离。它是一种有效的计算两个未知样本集的相似度的方法。与欧式距离不同的是它考虑到各种特性之间的联系(例如:一条关于身高的信息会带来一条关于体重的信息,因为两者是有关联的),并且是尺度无关的(scale-invariant),即独立于测量尺度。
马氏距离不受量纲的影响,两点之间的马氏距离与原始数据的测量单位无关;由标准化数据和中心化数据(即原始数据与均值之差)计算出的二点之间的马氏距离相同。马氏距离还可以排除变量之间的相关性的干扰。它的缺点是夸大了变化微小的变量的作用。
在统计学与概率论中,协方差矩阵(或称共变异矩阵)是一个矩阵,其每个元素是各个向量元素之间的方差。这是从标量随机变量到高维度随机向量的自然推广。
并且μi
即:
矩阵中的第(i,j)个元素是Xi与Xj的协方差。这个概念是对于标量随机变量方差的一般化推广。
尽管协方差矩阵很简单,可它却是很多领域里的非常有力的工具。它能导出一个变换矩阵,这个矩阵能使数据完全去相关(decorrelation)。从不同的角度看,也就是说能够找出一组最佳的基以紧凑的方式来表达数据。(完整的证明请参考瑞利商)。 这个方法在统计学中被称为主成分分析(principal components analysis),在图像处理中称为Karhunen-Loève 变换(KL-变换)。
注意:
1)马氏距离的计算是建立在总体样本的基础上的,这一点可以从上述协方差矩阵的解释中可以得出,也就是说,如果拿同样的两个样本,放入两个不同的总体中,最后计算得出的两个样本间的马氏距离通常是不相同的,除非这两个总体的协方差矩阵碰巧相同;
2)在计算马氏距离过程中,要求总体样本数大于样本的维数,否则得到的总体样本协方差矩阵逆矩阵不存在,这种情况下,用欧式距离来代替马氏距离,也可以理解为,如果样本数小于样本的维数,这种情况下求其中两个样本的距离,采用欧式距离计算即可。
3)还有一种情况,满足了条件总体样本数大于样本的维数,但是协方差矩阵的逆矩阵仍然不存在,比如A(3,4),B(5,6);C(7,8),这种情况是因为这三个样本在其所处的二维空间平面内共线(如果是大于二维的话,比较复杂???)。这种情况下,也采用欧式距离计算。
4)在实际应用中“总体样本数大于样本的维数”这个条件是很容易满足的,而所有样本点出现3)中所描述的情况是很少出现的,所以在绝大多数情况下,马氏距离是可以顺利计算的,但是马氏距离的计算是不稳定的,不稳定的来源是协方差矩阵,这也是马氏距离与欧式距离的最大差异之处。





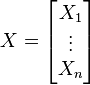

![马氏距离与协方差矩阵 \Sigma=\mathrm{E} \left[ \left( \textbf{X} - \mathrm{E}[\textbf{X}] \right) \left( \textbf{X} - \mathrm{E}[\textbf{X}] \right)^\top \right]](http://upload.wikimedia.org/math/1/8/1/1811f942680a72974597be42c28d31d2.png)
![马氏距离与协方差矩阵 = \begin{bmatrix} \mathrm{E}[(X_1 - \mu_1)(X_1 - \mu_1)] & \mathrm{E}[(X_1 - \mu_1)(X_2 - \mu_2)] & \cdots & \mathrm{E}[(X_1 - \mu_1)(X_n - \mu_n)] \\ \ \mathrm{E}[(X_2 - \mu_2)(X_1 - \mu_1)] & \mathrm{E}[(X_2 - \mu_2)(X_2 - \mu_2)] & \cdots & \mathrm{E}[(X_2 - \mu_2)(X_n - \mu_n)] \\ \ \vdots & \vdots & \ddots & \vdots \\ \ \mathrm{E}[(X_n - \mu_n)(X_1 - \mu_1)] & \mathrm{E}[(X_n - \mu_n)(X_2 - \mu_2)] & \cdots & \mathrm{E}[(X_n - \mu_n)(X_n - \mu_n)] \end{bmatrix}](http://upload.wikimedia.org/math/a/1/2/a12a573ecd1d853abd8c01fab9fccfbe.png)
















 2676
2676

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








