优先级队列（堆）-优快云博客

本文链接：https://blog.youkuaiyun.com/huapiaoy/article/details/144327868

（一）优先级队列的模拟实现

JDK1.8中的优先级队列底层是使用的堆这样的数据结构，而堆就是在“完全二叉树的基础上进行了调整”

堆的概念

如果有一个集合，我们把他的所有元素按完全二叉树的顺序存储方式存在一个一维数组中，同时堆分为大根堆和小根堆，大根堆就是这个完全二叉树的所有根结点都大于他的右左孩子结点，小根堆就是这个完全二叉树的所有根结点都小于他的右左孩子结点。

堆的性质：1.堆的某个结点值总是不大于或者不小于他的父节点的值 2.堆总是一颗完全二叉树

这就是一个小根堆和一个大根堆

堆的存储方式

从堆的概念可知，堆就是一个完全二叉树，所以我们用层序的规则，采用顺序的方式来高效存储

注：我们堆是完全二叉树，所以用顺序存储是很高效的，那如果是非完全二叉树，就不适合用顺序方式来进行存储，因为非完全二叉树就势必要存储空结点，这就会导致数组中要存储空结点，这就会导致空间利用率比较低

那接下来我们就要手写一个堆了，那在这之前，我们要了解几个规律：

我们假设i为结点在数组中的下标

1.如果i=0，则表示i为根结点，否则i节点的双亲结点为（i-1）/2

2.如果2*i+1小于结点个数，就说明结点i的左孩子下标为2*i+1，否则没有左孩子

3.如果2*i+2小于结点个数，就说明节点i的右孩子下标为2*i+2，否则没有右孩子

（二）堆的创建

1.向下调整

我们先来看一组例子

我们观察上图除了根节点，都符合小根堆的特性

所以我们需要向下调整：

1.让parent标记需要调整的节点，child表示parent的左孩子

2.如果parent的左孩子存在（child<array.length），如果右孩子存在，找到左右孩子中最小的孩子，然后与parent进行交换，交换后，我们要判断这个节点和他的孩子大小，如果小于他的孩子就继续（也就是继续向下调整）也就是继续parent=child;child=parent*2+1，否则我们就不需要调整这个子树了

注：在调整以parent为根的二叉树时，必须要满足parent的左子树和右子树已经是堆了，才可以继续向下调整（所以我们需要找到最后一个子树）我们可以使用上面的公式（i-1）/2，找到最后一个子树的根后（设为p），p-1就是他的前一个子树，就可以继续向下调整了

代码实现：

 public static void createHeap(int[] array){
        //最后一个节点的下标
        for (int parent=(array.length-1-1)/2;parent>=0;parent--){
            //向下调整
            siftDown(array,parent);
        }
    }
    private static void siftDown(int[] array,int parent) {
        //向下调整的前提是有左孩子
        int len=array.length;
        int child=parent*2+1;
        while(child<len){
            //判断是否有右孩子
            // 有右孩子就判断左右谁大
            if(child+1<len&&array[child]<array[child+1]){
                child=child+1;   //child永远指向最大的孩子
            }
            //判断两个孩子中的最大值是否比parent值大
            if(array[child]>array[parent]){
                //如果孩子大就交换，然后parent向下走继续判断
                swap(array,child,parent);
                parent=child;
                child=parent*2+1;
            } else{
                //如果parent大就不需要继续调整了
                break;
            }
        }
    }

时间复杂度：我们这里来分析一下我们说堆是一个完全二叉树，那他的高度就设为h，然后堆的最后一层节点是不需要向下调整的，那我们可以得知

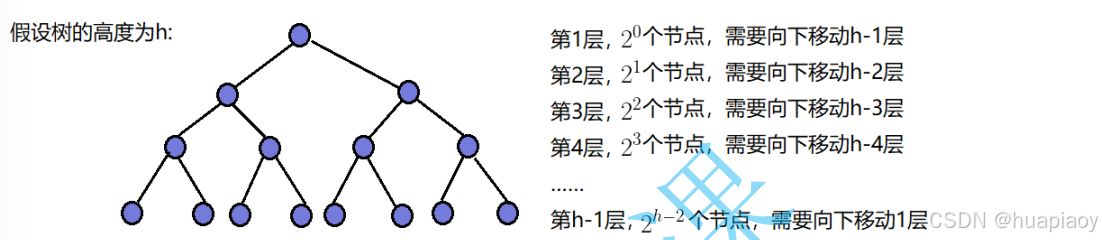
2^0*(h-1)+2^1*(h-2)+.......+2^h-2*(1)我们可以用错位相减法来得到

T（n）=2^h-1-h

我们可以得到n=2^h-1,h=log(n+1)

所以时间复杂度T(n)约等于n 空间复杂度为O(1)

（三）堆的插入

堆的插入一共分两步：

1.把插入元素放到最末尾(空间不够扩容)

2.向上调整，直到满足堆的性质

代码实现如下

public void push(int val){
        if (elem.length==usedSize){
            //满了就扩容
            Arrays.copyOf(elem, elem.length*2);
        }
        elem[usedSize]=val;
        siftUp(usedSize);//向上调整
        usedSize++;
    }

    private void siftUp(int child) {
        //向上调整只需要跟根节点做比较即可
        int parent=(child-1)/2;
        while(child>0){
        if(elem[parent]<elem[child]){
            swap(child,parent);
            child=parent;
            parent=(child-1)/2;
            }else {
            break;
            }
        }
    }

（四）堆的删除

堆删除的元素一定是对丁元素具体步骤如下：

1.将根元素与堆最后一个元素交换

2.把有效数据-1

3.根节点向下调整

代码实现如下：

 public int poll(){
        //先判空
        if(usedSize==0){
            return -1;
        }
        int oldVal=elem[0];
        swap(0,usedSize-1); //将根元素与堆最后一个元素交换
        usedSize--;
        siftDown(0,usedSize);
        return oldVal;
    }