java手写二叉堆

最新推荐文章于 2025-03-17 19:48:08 发布

huangshanchun

最新推荐文章于 2025-03-17 19:48:08 发布

阅读量847

点赞数

分类专栏：数据结构/算法文章标签： java 数据结构算法堆

本文链接：https://blog.youkuaiyun.com/huangshanchun/article/details/124538342

版权

数据结构/算法专栏收录该内容

32 篇文章

订阅专栏

本文详细介绍了二叉堆的概念，强调了它作为完全二叉树的特性。通过代码示例展示了如何在Java中实现大顶堆，包括添加元素（上浮操作）和删除元素（下沉操作）。此外，还提供了完整的MaxHeap类实现，用于演示堆的增删查改操作，并通过随机生成数据验证了其正确性。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

0 二叉堆的定义

由n个元素组成的序列{k1，k2，…，kn-1，kn}，当且仅当满足如下图关系时，称之为堆。可以简单理解为，所有父节满足要么都大于（大顶堆）或者都小于（小顶堆）左孩子和右孩子，注意点这里面没有要求左子树和右子树的关系和BST（二叉排序树）是有区别的。
在这里插入图片描述
**二叉堆是一棵完全二叉树（简单理解就是数组一层一层放，从左到右依次存放，只有上一层放满了才放下一层），**如下图所示大顶堆，可以使用数组来存储。考虑到数组下标是从0开始，对于一个节点位置i其父节点的位置parent(i)=(i-1)/2 ，其左孩子节点位置leftChild(i)=2i+1;其右孩子节点位置rightChild(i)=2i+2; 在这里插入图片描述

1 代码实现思路（大顶堆）

分两种情况：即添加数据和删除数据。
**先看添加数据思路：**将待添加数据加入数组尾部（数组容量不够要进行扩容），如下图所示添加一个新元素80进来，不难发现80要比其父节点要大，就不满足大顶堆条件，因此需要调整堆，也就是我们常说的siftUp（上浮操作），原理比较简单：不短的和其父节点比较，如果比起父节点大，就和父节点交换，并继续上浮至其比父节点或者已成为根节点则结束。80节点在数组中的下标为6，其父节点在数组下标getParent(6)=2，比较大小，80 比76大，80上浮到76；
80 又比77 ，80 和77 交换上浮至根节点，调整完则变成如下图所示。
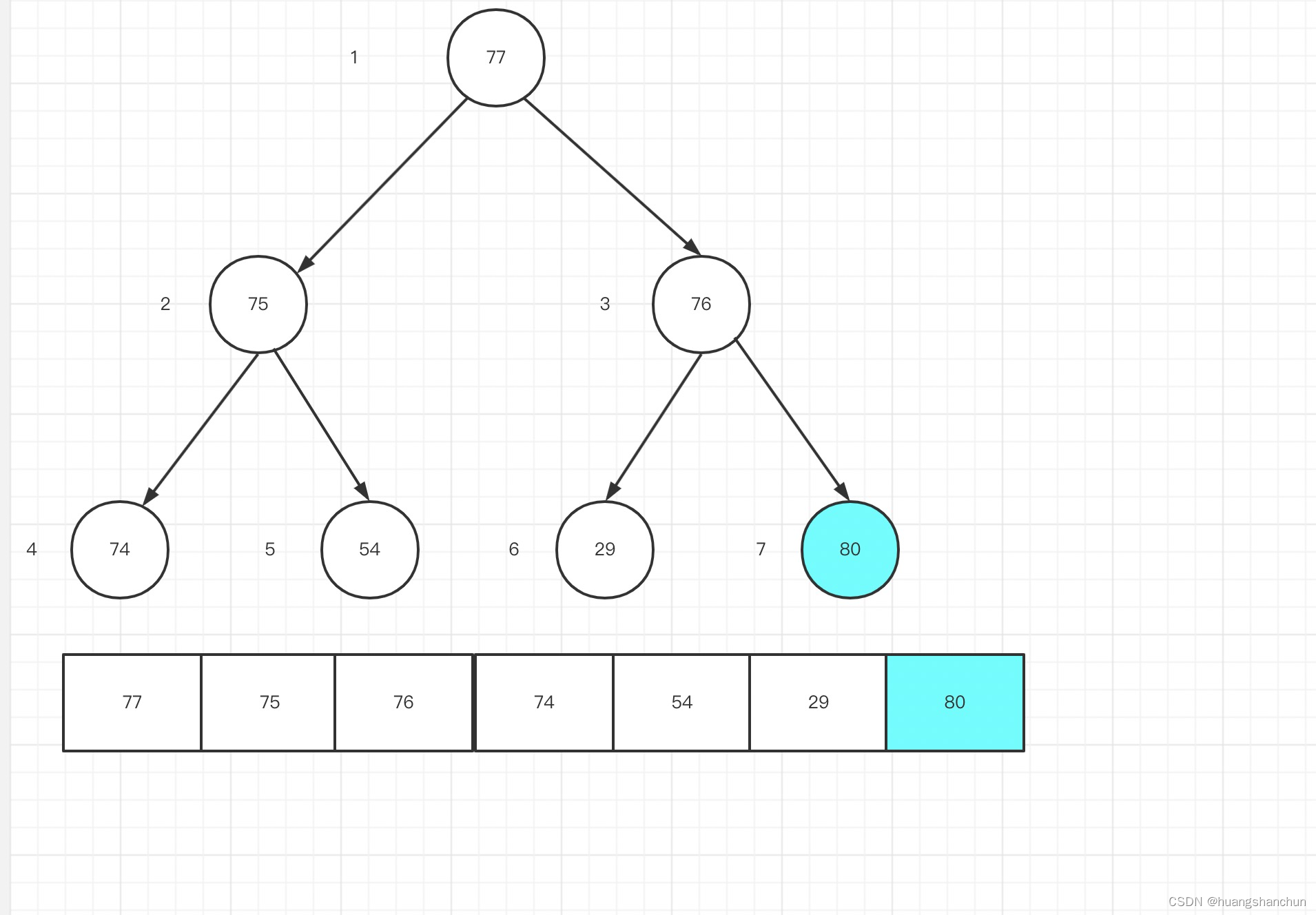
在这里插入图片描述

调整后堆



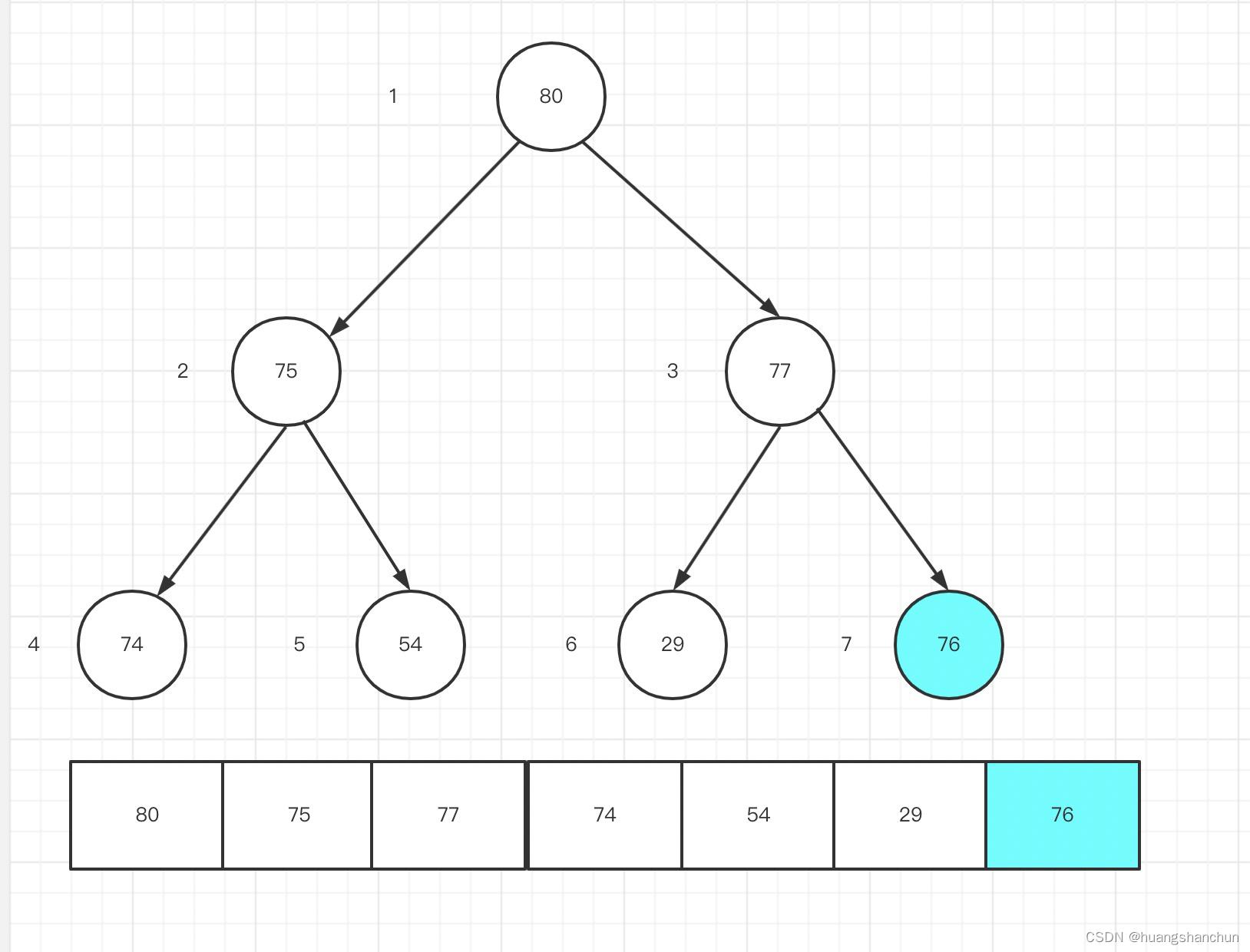
    //上浮过程，入参是上浮哪个节点
   private void siftUp(int k) {
        while (k > 0) {
            //找到其父节点
            int parent = getParent(k);
            if (getData(k).compareTo(getData(parent)) < 0)
                break;
            Object tmp = data[k];
            data[k] = data[parent];
            data[parent] = tmp;
            k = parent;
        }
    }

private int getParent(int k) {
        if (k <= 0) {
            throw new IllegalArgumentException(k + "not has parent");
        }
        return (k - 1) / 2;
    }

    private int getLeftChild(int k) {
        return 2 * k + 1;
    }

    private int getRightChild(int k) {
        return 2 * k + 2;
    }

删除数据：当删除堆顶元素
思路：删除堆顶元素data[0]，用最后一个数组填充，然后逐步siftDown（下沉），即：在其左孩子和右孩子找到最大元素和其交换，依次下沉至改节点没有左右子树或者都比左右子树大。
先删除上面堆顶77，将堆中最后一个数29放到堆顶，然后执行下下沉，29 的左右孩子中最大的是76（右孩子），29和右孩子76直接交换，交换后继续比较，发现其当前没有左右孩子则结束下沉。
在这里插入图片描述

  //下沉
    private void siftDown(int k) {
        while (getLeftChild(k) < size) {
            E parent = getData(k);
            int left = getLeftChild(k);
            int p = left;
            //比较左孩子和右孩子谁大
            if (left + 1 < size && getData(left + 1).compareTo(getData(left)) > 0) {
                p = left + 1;
            }
            E max = getData(p);
            //如果左右孩子的最大值都比父亲节点小，则结束
            if (parent.compareTo(max) > 0) {
                break;
            }
            //交换，继续执行
            Object tmp = data[p];
            data[p] = parent;
            data[k] = tmp;
            k = p;
        }
    }

2 完整代码实现

public class MaxHeap<E extends Comparable<E>> {
    private static final int DEFAULT_INITIAL_CAPACITY = 16;
    //堆元素存放
    public Object[] data;
    //堆元素数量
    private int size = 0;

    public MaxHeap() {
        data = new Object[DEFAULT_INITIAL_CAPACITY];
    }

    public int size() {
        return size;
    }

    public boolean isEmpty() {
        return size == 0;
    }

    public void add(E e) {
        if (size == data.length) {
            resize();
        }
        data[size] = e;
        size = size + 1;
        siftUp(size - 1);
    }

    private void resize() {
        Object[] newData = new Object[data.length * 2];
        System.arraycopy(data, 0, newData, 0, data.length);
        data = newData;
    }

    private int getParent(int k) {
        if (k <= 0) {
            throw new IllegalArgumentException(k + "not has parent");
        }
        return (k - 1) / 2;
    }

    private int getLeftChild(int k) {
        return 2 * k + 1;
    }

    private int getRightChild(int k) {
        return 2 * k + 2;
    }

    //上浮
    private void siftUp(int k) {
        while (k > 0) {
            int parent = (k - 1) / 2;
            if (getData(k).compareTo(getData(parent)) < 0)
                break;
            Object tmp = data[k];
            data[k] = data[parent];
            data[parent] = tmp;
            k = parent;
        }
    }

    //下沉
    private void siftDown(int k) {
        while (getLeftChild(k) < size) {
            E parent = getData(k);
            int left = getLeftChild(k);
            int p = left;
            //比较左孩子和右孩子谁大
            if (left + 1 < size && getData(left + 1).compareTo(getData(left)) > 0) {
                p = left + 1;
            }
            E max = getData(p);
            //如果左右孩子的最大值都比父亲节点小，则结束
            if (parent.compareTo(max) > 0) {
                break;
            }
            //交换，继续执行
            Object tmp = data[p];
            data[p] = parent;
            data[k] = tmp;
            k = p;
        }
    }

    public E peek() {
        if (isEmpty()) {
            return null;
        }
        return getData(0);
    }

    public E poll() {
        if (isEmpty()) {
            return null;
        }
        E ret = peek();
        //将尾节点放到头节点
        data[0] = data[size - 1];
        size = size - 1;
        siftDown(0);
        return ret;
    }

    private E getData(int index) {
        return (E) data[index];
    }

    public static void main(String[] args) {
        int n = 300;
        MaxHeap<Integer> maxHeap = new MaxHeap<>();
        Random random = new Random();
        for (int i = 0; i < n; i++) {
            maxHeap.add(random.nextInt(1000));
        }
        int[] arr = new int[n];
        for (int i = 0; i < n; i++) {
            arr[i] = maxHeap.poll();
        }
        for (int i = 1; i < n; i++) {
            System.out.println(arr[i]);
            if (arr[i - 1] < arr[i]) {
                throw new IllegalArgumentException("error");
            }
        }
    }

}