二叉树的各种遍历（非递归实现版本）

• 先序遍历

class TreeNode(object):
     def __init__(self, x):
         self.val = x
         self.left = None
         self.right = None
class Solution(object):
    # method 1
    def preorderTraversal_1(self, root):
        """
        :type root: TreeNode
        :rtype: List[int]
        """
        stack = []
        res = []
        if root:
            stack.append(root)
        while(stack):
            x=stack.pop(-1)
            res.append(x.val)
            if x.right:
                stack.append(x.right)
            if x.left:
                stack.append(x.left)
        print(res)
        return res
    # method 2
    def preorderTraversal_2(self, root):
        """
        :type root: TreeNode
        :rtype: List[int]
        """
        stack = []
        res = []
        while 1:
            while root:
                res.append(root.val)
                stack.append(root.right)
                root = root.left
            if stack==[]:
                break
            root = stack.pop(-1)
        print(res)
        return res
    # method 3
    def preorderTraversal_3(self, root):
        """
        :type root: TreeNode
        :rtype: List[int]
        """
        stack = []
        res = []
        while 1:
            while root:
                res.append(root.val)
                stack.append(root)
                root = root.left
            if stack==[]:
                break
            root = stack.pop(-1)
            root = root.right
        print(res)
        return res



if __name__ == '__main__':
    S = Solution()
    l1 = TreeNode(1)
    l2 = TreeNode(2)
    l3 = TreeNode(3)
    l4 = TreeNode(4)
    l5 = TreeNode(5)
    l6 = TreeNode(6)
    l7 = TreeNode(7)
    root = l1
    l1.left = l2
    l1.right = l3
    l2.left = l4
    l2.right = l5
    l3.left = l6
    l3.right = l7
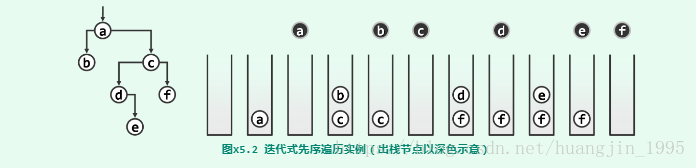
    z = S.preorderTraversal_1(root)

对于方法1，思路是，首先把根节点入栈，然后在循环里面：首先把根节点出栈，并访问根节点的值；判断根节点是否存在右孩子和左孩子（右顾左盼），并把右孩子和左孩子依次入栈，重新进入循环，根据FILO原则，左孩子先出栈，并访问其值；再判断左孩子的左右孩子情况，不断迭代。如下图所示：

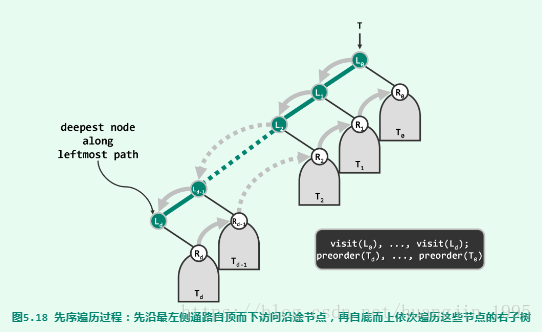
对于方法2，思路是，在内层while循环里，从根节点开始，首次访问该节点，然后把该节点的右孩子入栈，不断向左走，直到某个节点没有左孩子。这个时候，元素出栈，第一次出来的是最左边节点的右孩子（如果存在右孩子的话；不存在时出栈的是其父节点的右孩子）。外面的大循环就是使得每次从出栈的右孩子开始，继续按照沿着左侧链走的思想进行下去。算法退出的条件是栈为空。如下图所示：

对于方法3，思路其实和法2差不多，只不过入栈的是左侧链的节点本身。在左侧链走到底后，栈弹出来一个元素，并把该元素的右孩子重新传递内层循环的条件，再次按左侧链迭代。算法退出的条件是栈为空。

• 中序遍历

class TreeNode(object):
     def __init__(self, x):
         self.val = x
         self.left = None
         self.right = None
class Solution(object):
    def inorderTraversal_1(self, root):
        """
        :type root: TreeNode
        :rtype: List[int]
        """
        stack = []
        res = []
        while 1:
            while root:
                stack.append(root)
                root = root.left
            if stack==[]:
                break
            root = stack.pop(-1)
            res.append(root.val)
            root = root.right
        print(res)
        return res
if __name__ == '__main__':
    S = Solution()
    l1 = TreeNode(1)
    l2 = TreeNode(2)
    l3 = TreeNode(3)
    l4 = TreeNode(4)
    l5 = TreeNode(5)
    l6 = TreeNode(6)
    l7 = TreeNode(7)
    root = l1
    l1.left = l2
    l1.right = l3
    l2.left = l4
    l2.right = l5
    l3.left = l6
    l3.right = l7
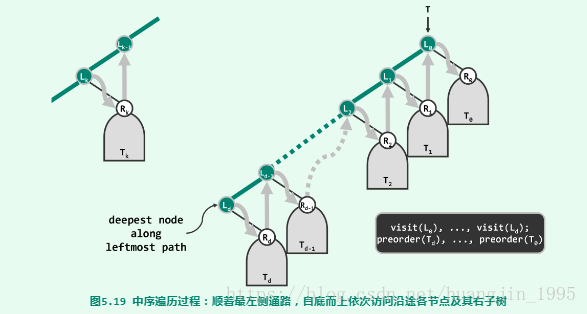
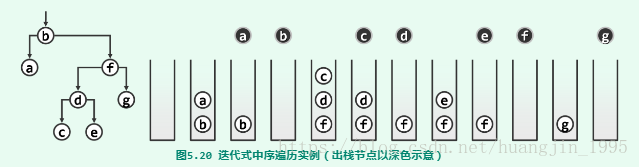
    z = S.inorderTraversal_1(root)

中序遍历的思路和先序遍历的思路3类型，首先是先沿着左侧链走，把沿途节点进栈，在达到最左端后，出栈，并访问其值，然后把该节点的右孩子赋给内层循环的变量，在右孩子处继续按左侧链思路走下去。直到栈空。如下图所示：

• 后序遍历

class TreeNode(object):
     def __init__(self, x):
         self.val = x
         self.left = None
         self.right = None
class Solution(object):
    # 借鉴前序遍历方法1的思路，最后把结果逆转
    def postorderTraversal_1(self, root):
        """
        :type root: TreeNode
        :rtype: List[int]
        """
        res=[]
        stack = [root]
        while stack:
            t = stack.pop()
            if t:
                res.append(t.val)
                stack.append(t.left)
                stack.append(t.right)
        print(res[::-1])
        return res[::-1]
    # 节点加一个标志符号组成二元组，构成栈的元素
    def postorderTraversal_2(self, root):
        res=[]
        stack=[(root,False)]
        while stack:
            t,flag = stack.pop()
            if t:
                if flag:
                    res.append(t.val)
                else:
                    stack.append((t, True))
                    stack.append((t.right, False))
                    stack.append((t.left, False))
        print(res)
        return res
    def postorderTraversal_3(self, root):
        """
        :type root: TreeNode
        :rtype: List[int]
        """
        res=[]
        stack = [root]
        while stack:
            t = stack.pop()
            if type(t) is TreeNode:
                stack.append(t.val)
                if t.right:
                    stack.append(t.right)
                if t.left:
                    stack.append(t.left)
            else:
                res.append(t)
        print(res)
        return res

    def postorderTraversal_4(self, root):
        res=[]
        if not root:
            return
        stackNode = []
        markNode = None
        node = root
        while stackNode or node:
           while node:
            stackNode.append(node)
            node = node.left
           node = stackNode.pop()
           if not node.right or node.right is markNode:
            #node  has no rightNode or node's rightNode has been checked
            res.append(node.val)
            markNode = node
            node = None
           else:
            stackNode.append(node)
            node = node.right
        print(res)
        return res
if __name__ == '__main__':
    S = Solution()
    l1 = TreeNode(1)
    l2 = TreeNode(2)
    l3 = TreeNode(3)
    l4 = TreeNode(4)
    l5 = TreeNode(5)
    l6 = TreeNode(6)
    l7 = TreeNode(7)
    root = l1
    l1.left = l2
    l1.right = l3
    l2.left = l4
    l2.right = l5
    l3.left = l6
    l3.right = l7
    z = S.postorderTraversal_1(root)

思路一：类似于先序遍历的方法一，首先根节点入栈，然后在大循环里出栈，并访问其值， 接着左孩子入栈，右孩子入栈；回到循环处，继续出栈、访问。。。最终结果刚好是后序遍历的逆序，所以反转后即可。

思路二：节点加一个标志符号组成二元组，构成栈的元素，首先根节点出栈，然后判断FALG是否为TRUE，否，则重新入栈，并令其flag为true，并把其右孩子，左孩子入栈，且其FLAG初始值均为False;接着继续进行上述操作，直到最左边的节点入栈，值为false，此时其出栈后判断再进栈变为true，此时无孩子入栈，继续循环，此时为true了，所以直接append结果；一直循环即可。

参考资料：https://blog.youkuaiyun.com/yangjingjing9/article/details/77054899