投影梯度下降算法PGD(Projected Gradient Descent)
![]() , P为投影算子,其根据具体的优化问题而定。比如:
, P为投影算子,其根据具体的优化问题而定。比如:
 , 投影算子为
, 投影算子为
AmsGrad (Adam的改进版)
 ,
,
其中是常量,而
是随迭代而变的,往往取值为
,
为常量
AdamNC (对Adam中的参数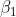 与
与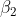 进行自适应调整)
进行自适应调整)
,
SAG方法(随机梯度均值)
针对SGD(随机梯度下降)方法的不足“收敛速度是亚线性的”,且梯度的方差很大,提出如下SAG方法:
在内存中为训练集的每个样本都维护一个旧的梯度
, 并将所有样本的历史梯度和记为d, 在训练过程中的第t次迭代时,从训练集中随机选取样本i, 利用第(t-1)次学得参数
计算样本i的梯度值
, 以
更新d, 然后同时以
更新样本i的梯度值,最后利用d来更新参数:
SVRG方法(方差消减的随机梯度)
针对SAG(随机梯度均值)的特点:具有线性收敛速度,但其只能适用于loss函数为光滑凸的情况,且需要为每个样本都保留梯度信息。提出SVAG方法,该方法可以无需为每个样本保留梯度信息,从而节省空间开销,更重要的是可用于非凸问题的优化。
每隔w次迭代对计算1次所有样本的梯度:,
为这w次迭代的
的均值,而在这w次迭代内利用上一个w次的
和
进行参数更新, 方式为:
ADMM(交替方向乘子法)
ADMM通常解决的是等式约束的优化问题,而且这个优化问题还有两个优化变量 x跟 z, 形式如下:
通过拉氏方法将其等价表示为无条件的最小化问题: , 最末项是为了增加该优化问题的凸性。
若该优化问题是凸的,则其有等价的对偶问题为,通过迭代如下两步实现该对偶问题的求解
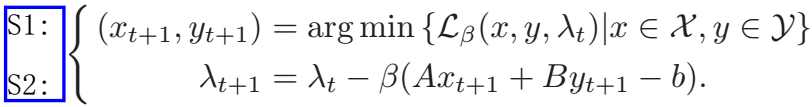
S1与相对应,S2与
相对应
从目标函数的可分离性可知,可将原问题子分为多个小问题,即有求解步骤:
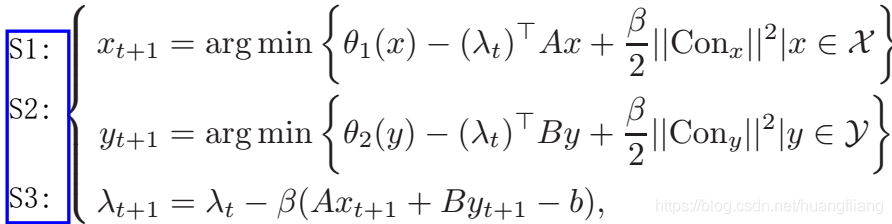
其中![]()




 本文探讨了一阶优化方法,包括投影梯度下降(PGD)、AmsGrad(Adam改进版)、AdamNC、SAG(随机梯度均值)、SVRG(方差消减的随机梯度)以及ADMM(交替方向乘子法),详细阐述了这些方法的工作原理和应用场景,对于理解和应用优化算法具有指导意义。
本文探讨了一阶优化方法,包括投影梯度下降(PGD)、AmsGrad(Adam改进版)、AdamNC、SAG(随机梯度均值)、SVRG(方差消减的随机梯度)以及ADMM(交替方向乘子法),详细阐述了这些方法的工作原理和应用场景,对于理解和应用优化算法具有指导意义。

















 2312
2312

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








