1. 叉积(wikipedia):两个向量的叉积是 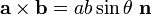 ,表示两个向量组成的平行四边形的面积, a(x1, y1) X b(x2, y2) = x1y2 – y1x2
,表示两个向量组成的平行四边形的面积, a(x1, y1) X b(x2, y2) = x1y2 – y1x2
2. 点是否在线段上。
先判断是否三点共线:假设判断点p是否在线段e(u,v), p,u,v 是三个点。首先构造pu,pv 向量,然后pu和pv的叉积为0,因为这是因为三点共线的话这两个向量夹角为0,所以叉积为0.
然后再判断是点是否在线段上:已经三点共线了,那么如果p在uv中间,必须有: (p.x-u.x)*(p.x-v.x)<0 || (p.y-u.y)*(p.y-v.y)<0 . 这就完成了点是否在线段上的判断。
3. 线段是否overlap(不包括共端点的情况)
假设是线段uv和线段pq
a. 计算u是否和pq共线,v是否和pq共线。都共线的话说明两条线段在同一条直线上。
b. 判断点u,v是否有一个在线段pq上(利用2的方法)
c. 如果上面两个都满足了,说明overlap,否则没有overlap
























 1163
1163

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








