人工智能之数学基础：向量组的秩

本文重点

在前面的课程中，我们学习了极大线性无关组，当我们搞懂极大线性无关组之后，我们就可以搞懂向量组的秩了。向量组的秩是一个核心概念，它揭示了向量组之间的线性关系及其生成的向量空间的维度。

向量组秩的定义

向量组的秩，简称秩，是指向量组中的极大线性无关组所含向量的个数。所谓极大线性无关组，是指在向量组中可以找到的一个部分组，这个部分组中的向量线性无关，且向量组中的每一个向量都可以由这个部分组线性表示。

具体来说，若向量组α1,α2,…,αs​中存在一个部分组αi1​,αi2​,…,αir​满足：

1. αi1​,αi2​,…,αir​线性无关；
2. 向量组中的每一个向量αj​（j=1,2,…,s）都可以由αi1​,αi2​,…,αir​线性表示。

则称αi1​,αi2​,…,αir​是向量组α1​,α2​,…,αs​的一个极大线性无关组，而r就是向量组α1​,α2​,…,αs​的秩，记作R(α1​,α2​,…,αs​)=r。

举例

我们前面学习了极大线性无关组，当我们求出一个向量组的极大线性无关组的时候，我们只需要数一下这个极大线性无关组中有多少个向量，有几个向量，秩就是多少。

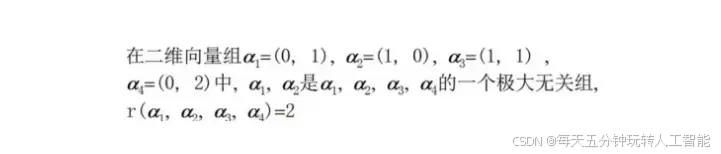
特殊：全由零向量组成向量组的秩为0

向量组秩的性质

向量组的秩具有一系列重要的性质，这些性质对于理解和应用向量组的秩至关重要