赛马问题----大学生作业

前言

大学生的作业

问题

64匹马和8条跑道，每次只允许最多8匹马同时比赛(假设每匹马每次比赛速度相同)，但是没有秒表不能计时，为最少要比多少次，才能选出最快的4匹马。

解题

正常的思路

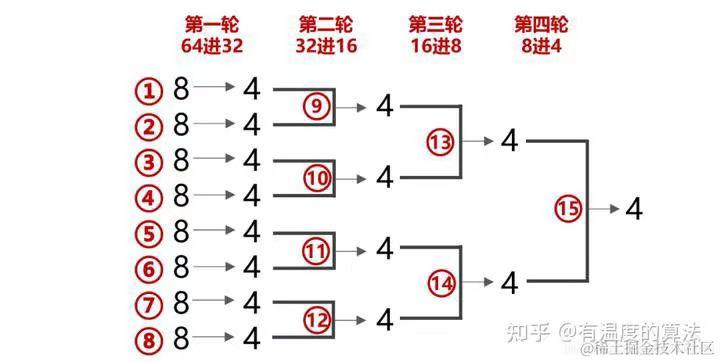
这样就需要比赛4轮15次，不是最优解

优解

第一步:将他们分为8组，来进行比赛,淘汰他们最后四名(最后四名肯定不是最快的四名)

这个是第一轮比赛:进行了8场比赛

第二步:取每一个组里面的第一名进行比赛,取出前四名,这样的话就可以排除后四名以及后四名他们后面的马了。如图,这是第二轮了:进行了1场比赛。

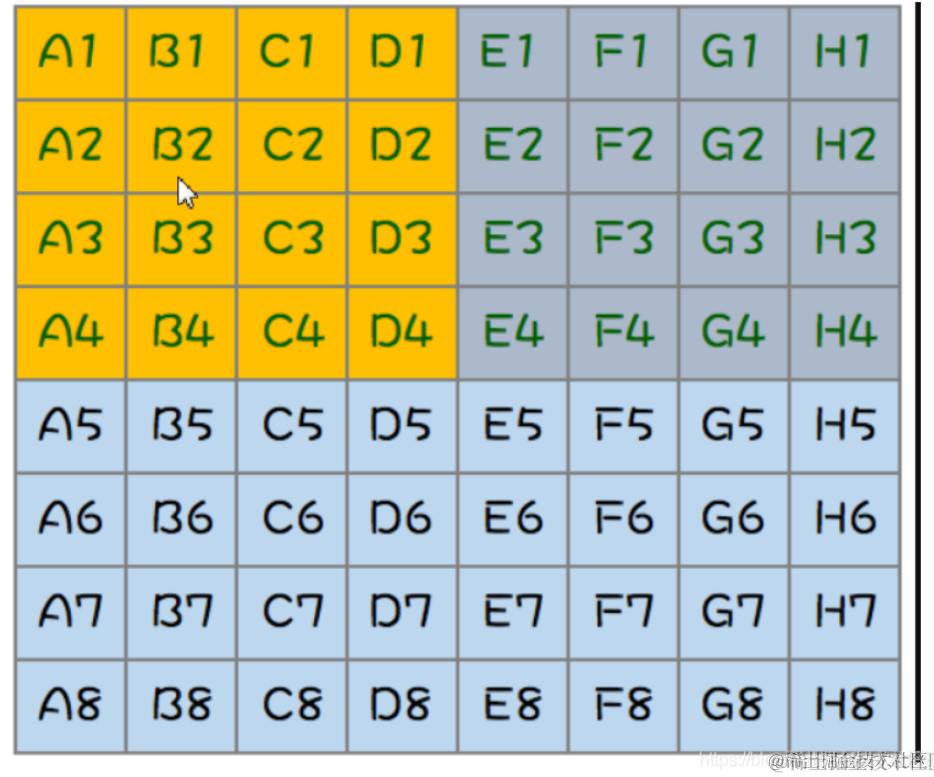
接着A1可以直接晋级了，因为他是跑的最快的，又可以排除D2、D3、D4,C3、C4，B4

第三步:这一轮会有加赛或者不加赛的情况。

现在只剩下除了A1(晋级)之后的马了，其中D1是最危险的，因为已经知道了两匹马比它快了，只要有一匹马还比他快(就是有一匹马比B1快或者比C1快)的话就不需要进行加赛了。当没有这种情况的话就需要进行加赛了。

说一说加赛的情况:

这个加赛就是除了A1,B1,C1三匹马之外的没有淘汰的马进行比赛来找出最快的一只作为第四名。

所以这一步可能进行一场比赛或者两场比赛。

结果

将每一步的比赛场数加起来为10或11轮。

最后

参考文献

经典面试题：64匹马,8个赛道,找出前4名最少比赛多少场?_64个运动员, 8个跑道, 如果要选出前四名, 至少跑几次?-优快云博客