深度学习基础与概念第三章注解_深度学习预测概率怎么没有渐变-优快云博客

为了将这些模型应用于密度估计问题,我们需要一种在给定观测数据集的情况下确定合适参数值的方法(主要聚焦于最大化似然函数)。

密度估计问题的本质

密度估计是要从观测数据中推断出数据的潜在概率分布。具体步骤是：

选择模型族：假设数据来自某个参数化的分布族（如正态分布、指数分布等）
确定参数：找到最能解释观测数据的参数值
得到密度函数：用估计的参数构建完整的概率密度函数

为什么需要参数估计

假设我们观察到一组身高数据，想要估计整个人群的身高分布：

模型假设：身高服从正态分布 N(μ, σ²)
问题：μ 和 σ² 是未知的
目标：从观测数据中找出最合适的 μ 和 σ² 值

没有参数值，我们只有一个"空壳"模型，无法进行预测或推断。

为什么最大似然是合理的

直观性：如果数据真的来自某个分布，那么使数据出现概率最大的参数最有可能是真实参数
频率主义解释：在大量重复实验中，真实参数使观测数据出现的概率最大
信息论解释：MLE等价于最小化模型分布与经验分布之间的KL散度

MLE等价于最小化模型分布与经验分布之间的KL散度经验分布具体例子：一维高斯分布

假设真实数据来自 $N (2, 1)$ ，我们用 $N(μ,1)N(\mu, 1)$ 来拟合：

import numpy as np
from scipy.stats import norm

# 生成数据
np.random.seed(42)
data = np.random.normal(2, 1, 1000)

# 经验KL散度
def empirical_kl(data, mu):
    cross_entropy = -np.mean(norm.logpdf(data, mu, 1))
    return cross_entropy  # 忽略常数项

# 遍历不同 μ
mus = np.linspace(0, 4, 100)
kls = [empirical_kl(data, mu) for mu in mus]

# KL 最小的 μ
optimal_mu = mus[np.argmin(kls)]  # ≈ 2.0

# MLE 估计
mle_mu = np.mean(data)  # ≈ 2.0

✅ 最小KL散度和最大似然估计给出相同的最优 $μ\mu$ ！

似然函数的定义

假设我们有 n 个观测数据样本 $x1,x2,…,xnx_1, x_2, \dots, x_n$ ，这些数据来自某个概率分布模型，该模型的参数为 θ。似然函数 $L(θ∣x1,x2,…,xn)L(\theta \mid x_1, x_2, \dots, x_n)$ 定义为：在给定参数 θ 的条件下，观测到这些具体数据样本的概率（或概率密度）。

数学上，它被写成：

$L(\theta \mid x_1, x_2, \dots, x_n) = f(x_1, x_2, \dots, x_n \mid \theta)$

其中：

$f(x1,x2,…,xn∣θ)f(x_1, x_2, \dots, x_n \mid \theta)$ 是随机变量 $X1,X2,…,XnX_1, X_2, \dots, X_n$ 的联合概率密度函数 (PDF) 或联合概率质量函数 (PMF)，取决于分布是连续型还是离散型。
竖线 “|” 表示条件：左侧是似然函数（参数 θ 给定数据），右侧是联合分布（数据给定参数 θ）。

为什么这样写？因为似然函数本质上就是将观测数据视为固定值，而将参数 θ 视为变量的联合概率函数。它“借用”了概率分布的形式，但颠倒了视角：

在概率中，我们固定 θ，计算数据出现的概率： $P(data∣θ)P(\text{data} \mid \theta)$ 。
在似然中，我们固定数据，评估不同 θ 的“合理性”：

$L(\theta \mid \text{data}) = P(\text{data} \mid \theta)$

这不是巧合，而是定义使然：似然函数直接等于给定 θ 时数据的联合概率（密度），因为它衡量了“数据在该 θ 下有多‘似然’（likely）出现”。

为什么不写成其他形式？

不能写成 $L(x∣θ)L(\mathbf{x} \mid \theta)$ ，因为这还是概率视角（数据变，θ 固定），而似然强调 θ 变，数据固定。
似然不是概率分布（即： $∫L(θ)dθ≠1\int L(\theta) d\theta \neq 1$ ），它只是一个相对度量，用于比较不同 θ。
这个写法突显了贝叶斯与频率学派的区别：在贝叶斯中，似然是后验的一部分： $p(θ∣x)∝L(θ∣x)⋅p(θ)p(\theta \mid \mathbf{x}) \propto L(\theta \mid \mathbf{x}) \cdot p(\theta)$ ,但 MLE 是纯频率方法，只用似然最大化。

[!NOTE]
注意对数似然函数仅依赖 $x_n$ 的 $N$ 个观测值的和 $∑n=1Nxn\sum_{n=1}^N x_n$ 。该值给出了数据在这一分布下的充分统计量（sufficient statistic）

直观理解

假设你有一组数据，想要估计某个未知参数。充分统计量的意思是：如果你知道了这个统计量的值，那么原始数据中就没有额外的信息能帮助你更好地估计这个参数了。换句话说，这个统计量已经“充分”概括了数据中关于参数的所有相关信息。

正式定义

设 $X1,X2,…,XnX_1, X_2, \dots, X_n$ 是来自分布 $f(x∣θ)f(x|\theta)$ 的随机样本，其中 $θ\theta$ 是未知参数。统计量 $T(X1,X2,…,Xn)T(X_1, X_2, \dots, X_n)$ 是关于参数 $θ\theta$ 的充分统计量，当且仅当在给定 $T$ 的值后，样本的条件分布不依赖于 $θ\theta$ 。

数学表达式为：

$P(X_1, X_2, \dots, X_n \mid T = t, \theta) = P(X_1, X_2, \dots, X_n \mid T = t)$

因子分解定理（Factorization Theorem）

判断充分统计量的一个实用方法是因子分解定理：

统计量 $T (X)$ 是充分统计量，当且仅当样本的联合概率密度函数可以分解为：

$f(x_1, x_2, \dots, x_n \mid \theta) = g(T(x_1, x_2, \dots, x_n), \theta) \cdot h(x_1, x_2, \dots, x_n)$

其中 $g$ 依赖于 $θ\theta$ 和 $T$ ，而 $h$ 不依赖于 $θ\theta$ 。

因子分解定理的核心思想

一个统计量 $T (X)$ 是关于参数 $θ\theta$ 的充分统计量，如果在知道 $T (X)$ 的情况下，原始样本数据中不再包含额外的关于 $θ\theta$ 的信息。

因子分解定理提供了一个“检查充分性”的实用方法：
只要能把联合概率分布写成依赖于 $T (X)$ 与 $θ\theta$ 的部分，以及完全不依赖 $θ\theta$ 的部分，就能判定 $T (X)$ 是充分统计量。

为什么要分解？

样本的联合分布函数为：

$f(x_1, x_2, \dots, x_n \mid \theta)$

这是数据与参数的完整关系。因子分解定理告诉我们，可以把它写成两部分：

$\theta)$ ：信息部分
- 只依赖于 $θ\theta$ 和统计量 $T (x)$ 。
- 说明所有关于 $θ\theta$ 的信息都集中在 $T (x)$ 中，数据再多也只是通过 $T (x)$ 来影响参数。
$h (x)$ ：无关部分
- 与 $θ\theta$ 无关，只依赖于原始数据 $x$ 。
- 这部分不能提供关于 $θ\theta$ 的信息，所以对参数推断没有用。

因此，一旦分解成立， $T (X)$ 就是充分统计量。

一个经典例子：泊松分布

设 $X1,X2,…,Xn∼i.i.d.Poisson(λ)X_1, X_2, \dots, X_n \overset{\text{i.i.d.}}{\sim} \text{Poisson}(\lambda)$ 。

单个样本的 pmf 为：

$f(x_i \mid \lambda) = \frac{\lambda^{x_i} e^{-\lambda}}{x_i!}, \quad x_i = 0, 1, 2, \dots$

联合分布为：

$f(x_1, \dots, x_n \mid \lambda) = \prod_{i=1}^n \frac{\lambda^{x_i} e^{-\lambda}}{x_i!} = \lambda^{\sum_{i=1}^n x_i} e^{-n \lambda} \cdot \frac{1}{\prod_{i=1}^n x_i!}$

现在看结构：

$g(T(x),λ)=λ∑x_ie−nλg(T(x), \lambda) = \lambda^{\sum x\_i} e^{-n\lambda}$ （依赖 $λ\lambda$ 和 $T(x)=∑xiT(x)=\sum x_i$ ）
$\frac{1}{\prod x_i!}$ （只依赖数据，不依赖 $λ\lambda$ ）

由因子分解定理可知， $\sum_{i=1}^n X_i$ 是 $λ\lambda$ 的充分统计量。

直观理解

如果我们知道了 $∑Xi\sum X_i$ ，就已经包含了所有和 $λ\lambda$ 有关的信息；
剩下的细节（比如每个 $X_i$ 的排列方式）只影响 $h (x)$ ，但它和 $λ\lambda$ 无关；
所以对于参数估计来说， $∑Xi\sum X_i$ 已经足够，原始数据再详细也没用。

总结

因子分解定理的意义：

提供了一个判断“充分性”的操作性工具。
本质上说明了：一个统计量是充分的，当它能捕获所有与参数相关的信息，剩余数据部分与参数无关。

重要性质

数据压缩：充分统计量实现了无损的数据压缩，用更简单的形式保留了所有关于参数的信息。
最小充分统计量：在所有充分统计量中，维数最小的称为最小充分统计量。
与估计的关系：任何好的参数估计量都应该是充分统计量的函数（Rao-Blackwell 定理）。

[!NOTE]
对于单个实数变量,能够使它的熵最大化的分布就是高斯分布。这一性质对于多元高斯分布同样适用.当我们考虑多个随机变量之和的时候, 同样会用到高斯分布

为什么必须是高斯分布（最大熵原理）

数学证明的核心思路

变分法与拉格朗日乘数法

我们要解决的是一个约束优化问题：

目标：最大化微分熵

$-\int p(x) \log p(x) \, dx$

约束条件：

归一化约束：

$\int p(x) \, dx = 1$
均值约束：

$\int x \, p(x) \, dx = \mu$
方差约束：

$\int (x-\mu)^2 p(x) \, dx = \sigma^2$

构造拉格朗日函数：

$dx−σ2)\mathcal{L} = -\int p(x) \log p(x)\, dx - lambda_1 \left( \int p(x)\, dx - 1 \right) - \lambda_2 \left( \int x p(x)\, dx - \mu \right) - \lambda_3 \left( \int (x-\mu)^2 p(x)\, dx - \sigma^2 \right)$

对 $p (x)$ 做变分并令其为零：

$\frac{\delta \mathcal{L}}{\delta p} = -\log p(x) - 1 - \lambda_1 - \lambda_2 x - \lambda_3 (x-\mu)^2 = 0$

解得：

$\exp \left( -1 - \lambda_1 - \lambda_2 x - \lambda_3 (x-\mu)^2 \right)$

通过约束条件解出拉格朗日乘数，最终得到：

$\frac{1}{\sqrt{2\pi \sigma^2}} \exp \!\left(-\frac{(x-\mu)^2}{2\sigma^2}\right)$

这正是高斯分布。

为什么不是其他分布？

数学唯一性
变分法给出的解是唯一的，在约束条件下满足最大熵的概率分布形式只能是高斯。
指数族一般结论
- 给定矩约束时，最大熵分布必定属于指数族
- 约束前两个矩（均值与方差） ⇒ 高斯分布
- 其他矩约束则对应其他分布（如拉普拉斯分布、指数分布等）
常见反例的限制
- 均匀分布：只能在有界区间上定义，不能满足实数轴上方差有限的条件
- 指数分布：只有一个参数，不能同时满足均值和方差两个独立约束
- 拉普拉斯分布：最大熵条件对应 $L^1$ 约束（绝对偏差），而不是方差
- t 分布：重尾，方差可能不存在，不满足有限方差约束

多元情况推广

对于多元情况，约束为：

均值：

$\mathbb{E}[X] = \mu$
协方差矩阵：

$\text{Cov}[X] = \Sigma$

同样的变分过程得到：

$\propto \exp \!\left(-\tfrac{1}{2} (x-\mu)^\top \Sigma^{-1} (x-\mu)\right)$

即 多元高斯分布。

高斯分布是最大熵分布，这不是偶然，而是数学必然：

在均值与方差已知的条件下，只有高斯分布能实现最大熵。
这也解释了：

中心极限定理的信息论解释：

多个独立信息源的叠加自然趋向于高斯分布
这不是偶然，而是熵最大化的必然结果
自然界"选择"了信息熵最大的状态

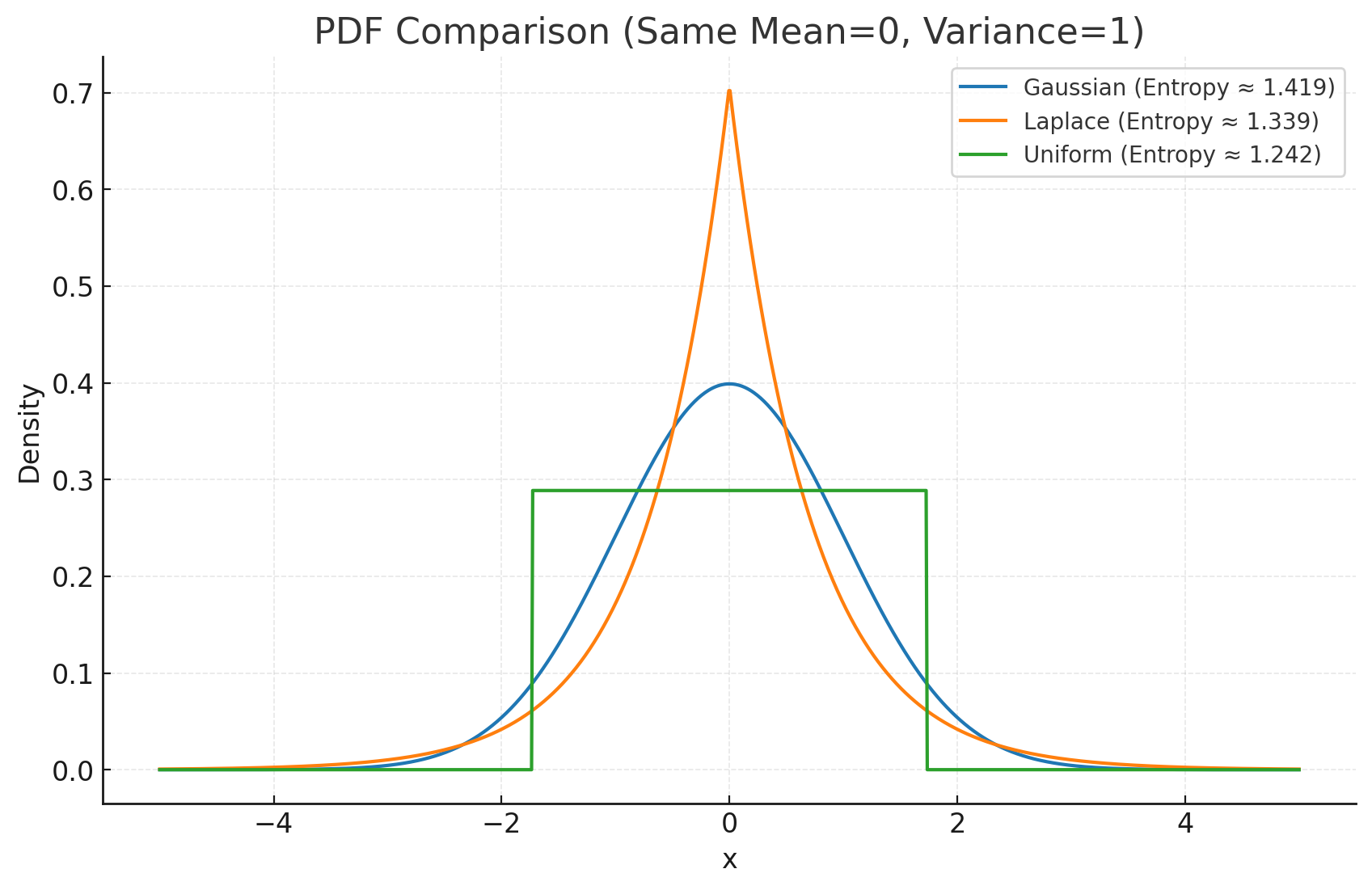
这张图展示了 高斯分布、拉普拉斯分布、均匀分布 在相同均值（0）和方差（1）下的概率密度函数 (PDF)，并标注了对应的熵值：

高斯分布 (Gaussian)：熵最大
拉普拉斯分布 (Laplace)：熵较小，因为分布在中心更尖锐，两侧更厚尾
均匀分布 (Uniform)：熵比拉普拉斯大，但仍小于高斯，因为尾部突然截断

👉 直观结论：在给定均值和方差约束下，高斯分布的熵始终最大，因此是“最不确定”、信息量最丰富的分布。

[!NOTE]
$Δ2=(x−μ)TΣ−1(x−μ)\Delta^2=(x-\mu)^{\mathrm{T}} \Sigma^{-1}(x-\mu)$
其中，量 $Δ\Delta$ 称为 $μ\boldsymbol{\mu}$ 到 $x\boldsymbol{x}$ 的马哈拉诺比斯距离（Mahalanobis distance）。当 $Σ\boldsymbol{\Sigma}$ 为单位矩阵时，它退化为欧氏距离。高斯分布在 $x\boldsymbol{x}$ 空间的曲面上是常数，因为该二次型为常数。
首先，注意可以不失一般性地假设矩阵 $Σ\boldsymbol{\Sigma}$ 为对称矩阵，因为任何非对称的成分都会从指数中消失（见习题3．11）。考虑协方差矩阵的特征方程：
$Σui=λiui\boldsymbol{\Sigma} \boldsymbol{u}_i=\lambda_i \boldsymbol{u}_i$

高斯分布的几何形式

一维高斯分布的几何形状

一维高斯分布 $N(μ,σ2)N(\mu, \sigma^2)$ 的概率密度函数为：

$\frac{1}{\sqrt{2\pi\sigma^2}} \exp \!\left( -\frac{(x-\mu)^2}{2\sigma^2} \right)$

几何特征：

钟形曲线：关于均值 $μ\mu$ 对称
拐点：在 $\mu \pm \sigma$ 处有拐点
68-95-99.7 规则：
- 约 68% 的数据在 $μ±σ\mu \pm \sigma$ 内
- 约 95% 的数据在 $μ±2σ\mu \pm 2\sigma$ 内
- 约 99.7% 的数据在 $μ±3σ\mu \pm 3\sigma$ 内

多元高斯分布的几何形状

多元高斯分布的概率密度函数为：

$\frac{1}{(2\pi)^{n/2} |\Sigma|^{1/2}} \exp \!\left( -\tfrac{1}{2} (x-\mu)^\top \Sigma^{-1} (x-\mu) \right)$

等概率密度面

指数项中的二次型：

$Δ2=(x−μ)TΣ−1(x−μ)\Delta^2=(x-\mu)^{\mathrm{T}} \Sigma^{-1}(x-\mu)$

定义了等概率密度面。

二维情况（n=2）：椭圆
$(x1−μ1)2σ12+(x2−μ2)2σ22+交叉项=c\frac{(x_1-\mu_1)^2}{\sigma_1^2} + \frac{(x_2-\mu_2)^2}{\sigma_2^2} + \text{交叉项} = c$

三维情况（n=3）：椭球面
$(x1−μ1)2σ12+(x2−μ2)2σ22+(x3−μ3)2σ32+交叉项=c\frac{(x_1-\mu_1)^2}{\sigma_1^2} + \frac{(x_2-\mu_2)^2}{\sigma_2^2} + \frac{(x_3-\mu_3)^2}{\sigma_3^2} + \text{交叉项} = c$

高维情况：超椭球面

核心思想：

高斯分布的概率密度完全由马哈拉诺比斯距离的平方 $Δ2\Delta^2$ 决定
相同 $Δ2\Delta^2$ 值的所有点具有相同的概率密度
这些点构成了椭球面族，这就是等概率密度曲面

二维情况：
- 当 $Σ=σ2I\Sigma = \sigma^2 I$ 时：等概率线是同心圆
- 当 $Σ\Sigma$ 为对角矩阵时：等概率线是椭圆，且轴与坐标轴平行
- 当 $Σ\Sigma$ 是一般矩阵时：等概率线是旋转的椭圆
三维情况：
等概率密度面是椭球面，其形状与方向由协方差矩阵 $Σ\Sigma$ 决定。

协方差矩阵的几何意义

协方差矩阵的特征值分解： $Σ=QΛQ⊤\Sigma = Q \Lambda Q^\top$

特征向量 $Q$ ：决定椭圆/椭球的主轴方向
特征值 $Λ\Lambda$ ：决定各主轴的伸展程度
第 $i$ 个特征值 $λi\lambda_i$ 对应第 $i$ 个主轴的方差

几何变换视角

多元高斯分布可以视为标准正态分布 $N (0, I)$ 经过以下变换：

平移： $\to x + \mu$ （改变中心）
线性变换： $\to A x$ ，其中 $AA⊤=ΣAA^\top = \Sigma$ （改变形状和方向）

实际意义

这种几何形式使得多元高斯分布：

直观可视化：椭圆/椭球直观展示数据分布
参数解释：协方差矩阵直接对应几何形状
计算便利：许多推导和计算可转化为几何问题
应用广泛：如聚类分析、PCA、卡尔曼滤波等都依赖这种几何理解

马哈拉诺比斯距离的含义

基本定义

$Δ2=(x−μ)TΣ−1(x−μ)\Delta^2=(x-\mu)^{\mathrm{T}} \Sigma^{-1}(x-\mu)$

这个距离衡量的是点 x 到分布中心 μ 的"标准化"距离：

几何直觉：

不是简单的欧氏距离，而是考虑了数据分布形状的距离
在数据变化大的方向上，相同的物理距离对应更小的马哈拉诺比斯距离
在数据变化小的方向上，相同的物理距离对应更大的马哈拉诺比斯距离

与欧氏距离的关系

当 Σ = I（单位矩阵）时：
$Δ2=(x−μ)T(x−μ)=∥x−μ∥2\Delta^2 = (x-\mu)^{\mathrm{T}}(x-\mu) = \|x-\mu\|^2$
这正是欧氏距离的平方！

一般情况下：
马哈拉诺比斯距离 = 在"拉直"数据后的欧氏距离

等概率密度曲面

为什么是常数曲面？

多元高斯分布的概率密度函数：
$\propto \exp\left(-\frac{1}{2}\Delta^2\right)$

关键观察：

当 $Δ2=c\Delta^2 = c$ （常数）时， $\text{常数}$
因此等概率密度面就是 $Δ2=c\Delta^2 = c$ 的曲面
这些曲面是同心的椭球面

几何形状

二维：椭圆族
三维：椭球面族
高维：超椭球面族

协方差矩阵的特征分解

特征方程

$Σui=λiui\Sigma u_i = \lambda_i u_i$

这告诉我们：

特征向量 $u_i$ ：椭球的主轴方向
特征值 $λi\lambda_i$ ：对应主轴方向的方差大小

几何解释

坐标变换视角：
设 $Σ=UΛUT\Sigma = U\Lambda U^T$ ，其中：

$U = [u_1, u_2, ..., u_n]$ ：特征向量矩阵
$Λ=diag(λ1,λ2,...,λn)\Lambda = \text{diag}(\lambda_1, \lambda_2, ..., \lambda_n)$ ：特征值对角矩阵

新坐标系：
令 $U^T(x-\mu)$ ，则：
$Δ2=yTΛ−1y=∑i=1nyi2λi\Delta^2 = y^T\Lambda^{-1}y = \sum_{i=1}^n \frac{y_i^2}{\lambda_i}$

这是标准椭球方程！

具体例子

二维情况

假设：
$Σ=[4222]\Sigma = \begin{bmatrix} 4 & 2 \\ 2 & 2 \end{bmatrix}$

特征值分解：

$λ1=5.236\lambda_1 = 5.236$ ， $u1=[0.8510.526]u_1 = \begin{bmatrix} 0.851 \\ 0.526 \end{bmatrix}$
$λ2=0.764\lambda_2 = 0.764$ ， $u2=[−0.5260.851]u_2 = \begin{bmatrix} -0.526 \\ 0.851 \end{bmatrix}$

几何意义：

椭圆的长轴方向： $u_1$ ，半轴长度： $λ1=2.29\sqrt{\lambda_1} = 2.29$
椭圆的短轴方向： $u_2$ ，半轴长度： $λ2=0.87\sqrt{\lambda_2} = 0.87$
椭圆相对于坐标轴旋转了约 $32°$

为什么协方差矩阵可以假设为对称？

数学原因

对于任意矩阵 $A$ ，在二次型 $x^TAx$ 中：
$xTAx=xT(A+AT2)xx^TAx = x^T\left(\frac{A + A^T}{2}\right)x$

关键点：

只有对称部分 $A+AT2\frac{A + A^T}{2}$ 影响二次型的值
非对称部分 $A−AT2\frac{A - A^T}{2}$ 对二次型没有贡献

为什么非对称成分会"消失".

任意矩阵的对称分解

对于任意方阵 $A$ ，都可以唯一分解为：
$\frac{A + A^T}{2} + \frac{A - A^T}{2} = A_{\text{sym}} + A_{\text{skew}}$

其中：

$Asym=A+AT2A_{\text{sym}} = \frac{A + A^T}{2}$ 是对称部分
$Askew=A−AT2A_{\text{skew}} = \frac{A - A^T}{2}$ 是反对称部分

二次型中反对称部分的贡献

对于任意向量 $\mu$ ，计算二次型：

$vTAv=vT(Asym+Askew)v=vTAsymv+vTAskewvv^T A v = v^T (A_{\text{sym}} + A_{\text{skew}}) v = v^T A_{\text{sym}} v + v^T A_{\text{skew}} v$

关键计算：
$vTAskewv=vT(A−AT2)vv^T A_{\text{skew}} v = v^T \left(\frac{A - A^T}{2}\right) v$

$\frac{1}{2}(v^T A v - v^T A^T v)$

$\frac{1}{2}(v^T A v - (v^T A^T v)^T)$

$\frac{1}{2}(v^T A v - v^T A v) = 0$

结论：反对称矩阵的二次型恒等于零！

物理直觉

协方差矩阵 $Σij=Cov(Xi,Xj)\Sigma_{ij} = \text{Cov}(X_i, X_j)$ 天然满足对称矩阵：
$Σij=Cov(Xi,Xj)=Cov(Xj,Xi)=Σji\Sigma_{ij} = \text{Cov}(X_i, X_j) = \text{Cov}(X_j, X_i) = \Sigma_{ji}$

二次型理论

这个结果是二次型理论的基本结果：

二次型 $x^T A x$ 完全由 $A$ 的对称部分决定
反对称部分对二次型没有任何影响
这在优化理论、微分几何等领域都有重要应用

线性代数视角

在线性代数中：

对称矩阵：可以表示椭球、抛物面等二次曲面
反对称矩阵：表示旋转、剪切等保距变换
在二次型中，只有"形状"信息（对称部分）重要，"旋转"信息（反对称部分）被忽略

考虑协方差矩阵：
$Σ=[4334]\Sigma = \begin{bmatrix} 4 & 3 \\ 3 & 4 \end{bmatrix}$

数据的"椭圆云"：

数据点不是随机散布的
而是形成一个椭圆形的云团
椭圆有长轴和短轴方向

主轴方向的具体含义

第一主轴（长轴）

方向：数据变化最大的方向
特点：沿这个方向，数据点分散得最开
对应：最大特征值 $λ1\lambda_1$ 的特征向量 $u_1$

第二主轴（短轴）

方向：数据变化次大的方向（与第一主轴垂直）
特点：沿这个方向，数据点相对聚集
对应：第二大特征值 $λ2\lambda_2$ 的特征向量 $u_2$

高维情况

在 $n$ 维空间中有 $n$ 个主轴方向：

$u_1$ ：第1主轴（方差最大）
$u_2$ ：第2主轴（方差次大）
…
$u_n$ ：第n主轴（方差最小）

为什么会有这些方向？

变量间的相关性

根本原因：变量之间的相关关系产生了方向性

举例：

身高 vs 体重数据：
- 两者正相关 → 数据沿对角线方向延伸
- 如果完全无关 → 数据呈圆形分布，无明显方向

[!NOTES]
讲一讲核密度和K近邻来估计密度函数

好的，我由浅入深地讲解这个基本原理，以及它如何成为核密度估计和K近邻密度估计的理论基础。

第一层：直觉理解

最简单的类比

想象你在一个黑暗的房间里，想知道某个位置的人群密度有多高：

方法1： 在那个位置画一个圆圈，数数圈内有多少人
方法2： 站在那个位置，看看最近的10个人距离你有多远

这就是密度估计的两种基本思路！

核心直觉

密度高的地方 = 附近样本点多的地方

第二层：数学化这个直觉

基本设定

有N个数据点： $x_1, x_2, ..., x_N$
想知道某个位置x处的密度 $p (x)$ 有多大

关键洞察

如果我们在点x周围画一个小区域 $R\mathcal{R}$ ：

$区域内的概率=∫Rp(x)dx\text{区域内的概率} = \int_{\mathcal{R}} p(x)dx$

这是什么意思？

就像掷飞镖，这个积分告诉我们"飞镖落在这个区域内的概率是多少"
如果这个区域密度很高，概率就大；密度低，概率就小

第三层：从概率到计数

核心转换

现在关键来了！我们有N个实际的数据点，这些点落在区域 $R\mathcal{R}$ 内的期望个数是：

$E[区域内点的个数]=N×P\mathbb{E}[\text{区域内点的个数}] = N \times P$

其中 $\int_{\mathcal{R}} p(x)dx$

为什么？

每个点落入区域的概率是P
有N个独立的点
所以期望总数 = N × P

这就像扔N次硬币，每次正面概率是P，期望正面次数就是NP。

第四层：反推密度

关键反推

如果实际观察到区域内有K个点，那么：
$\approx NP$

所以：
$\approx \frac{K}{N}$

最终密度估计

如果区域很小，密度在区域内近似常数：
$\int_{\mathcal{R}} p(x)dx \approx p(x) \times V$

其中V是区域体积。

因此：
$\approx \frac{P}{V} \approx \frac{K}{NV}$

这就是密度估计的万能公式！

第五层：两种不同的实现策略

现在我们有了公式 $\approx \frac{K}{NV}$ ，但K和V怎么确定呢？

策略1：固定V，数K（核密度估计的思路）

做法： 固定一个区域大小V（比如半径为h的圆）
数K： 统计这个固定区域内有多少个样本点
问题： 在样本稀少的地方，K可能为0，估计很不稳定

策略2：固定K，算V（K近邻的思路）

做法： 固定要找的近邻个数K（比如最近的5个点）
算V： 计算包含这K个点需要多大的区域
优势： 保证了统计的稳定性，因为总是有K个点

第六层：具体算法实现

核密度估计的完整实现

不是简单的数点，而是加权平均：

$p^(x)=1N∑i=1N1hK(x−xih)\hat{p}(x) = \frac{1}{N} \sum_{i=1}^{N} \frac{1}{h} K\left(\frac{x - x_i}{h}\right)$

为什么这样做？

$K(⋅)K(\cdot)$ 是核函数，给不同距离的点不同权重
距离x近的点权重大，远的点权重小
h控制"近"的定义（带宽）

K近邻的完整实现

$p^(x)=kN⋅Vk(x)\hat{p}(x) = \frac{k}{N \cdot V_k(x)}$

其中 $V_k(x)$ 是包含x的k个最近邻所需的区域体积。

第七层：为什么这个基础理论如此重要？

统一的理论框架

这个 $\approx \frac{K}{NV}$ 公式揭示了：

所有密度估计方法的本质：都是在平衡K和V
偏差-方差权衡：
- V太小（或K太小）→ 方差大，估计不稳定
- V太大（或K太大）→ 偏差大，过度平滑
维数灾难的根源：高维空间中，要么V很大，要么K很小

算法设计的指导

核密度估计：通过选择合适的核函数和带宽来平衡
K近邻：通过选择合适的K值来平衡

基于这个图片内容，我来详细讲解核密度估计技术的具体实现过程和关键概念。

核密度估计的构建过程

第一步：定义基础区域和核函数

超小立方体的定义：
对于希望确定概率密度的点x，将区域 $R\mathcal{R}$ 取为以点x为中心的超小立方体。

Parzen窗核函数：
$,D0,其他k(\mathbf{u}) = \begin{cases} 1, & |\mathbf{u}_i| \leq 1/2, \; i=1,\cdots,D \\ 0, & \text{其他} \end{cases}$

核函数的几何意义：

这是一个以原点为中心的单位立方体
在立方体内函数值为1，外部为0
这种核函数称为Parzen窗（Parzen window）

第二步：计算区域内的点数

点数统计公式：
$\sum_{n=1}^{N} k\left(\frac{\mathbf{x} - \mathbf{x}_n}{h}\right) \quad (1)$

公式解释：

如果数据点 $xn\mathbf{x}_n$ 位于以点x为中心、边长为h的立方体内
那么 $k((x−xn)/h)k((\mathbf{x}-\mathbf{x}_n)/h)$ 将为1，否则为0
K就是该立方体内数据点的总数

第三步：密度估计公式

最终密度估计：
$p(x)=1N∑n=1N1hDk(x−xnh)(3.183)p(\mathbf{x}) = \frac{1}{N} \sum_{n=1}^{N} \frac{1}{h^D} k\left(\frac{\mathbf{x} - \mathbf{x}_n}{h}\right) \quad (3.183)$

公式推导：

将式(1)代入基本公式 $p(x)=KNVp(\mathbf{x}) = \frac{K}{NV}$
D维空间中边长为h的超立方体体积： $V = h^D$
因此得到最终的密度估计公式

关键概念解析

1. 体积计算

D维超立方体体积公式：
$V = h^D$

这解释了为什么公式中有 $1hD\frac{1}{h^D}$ 项。

2. 核函数的对称性

重新解释估计过程：
利用核函数 $k(u)k(\mathbf{u})$ 的对称性，我们可以不再将其视为以点x为中心的单个立方体，而是视为以N个数据点 $xn\mathbf{x}_n$ 为中心的N个立方体的总和。

新的理解角度：

在每个数据点 $xn\mathbf{x}_n$ 处放置一个边长为h的立方体
每个立方体对密度的贡献是 $1NhD\frac{1}{Nh^D}$
点x处的总密度是所有包含x的立方体贡献的总和

从Parzen窗到一般核密度估计

Parzen窗的局限性

硬边界： 立方体边界处的突然截断
不可微： 在边界处不可导
视觉效果差： 产生块状的密度估计

改进方向

更平滑的核函数选择：

高斯核：
$k(u)=1(2π)D/2exp⁡(−∣u∣22)k(\mathbf{u}) = \frac{1}{(2\pi)^{D/2}} \exp\left(-\frac{|\mathbf{u}|^2}{2}\right)$

Epanechnikov核：
$∣u∣≤10otherwisek(\mathbf{u}) = \begin{cases} \frac{3}{4}(1-|\mathbf{u}|^2) & \text{if } |\mathbf{u}| \leq 1 \\ 0 & \text{otherwise} \end{cases}$

核密度估计的一般形式

通用公式

$p^(x)=1N∑n=1N1hDK(x−xnh)\hat{p}(\mathbf{x}) = \frac{1}{N} \sum_{n=1}^{N} \frac{1}{h^D} K\left(\frac{\mathbf{x} - \mathbf{x}_n}{h}\right)$

其中 $K(⋅)K(\cdot)$ 是任意满足 $∫K(u)du=1\int K(\mathbf{u})d\mathbf{u} = 1$ 的核函数。

核函数的一般要求

归一化： $∫K(u)du=1\int K(\mathbf{u})d\mathbf{u} = 1$
对称性： $K(u)=K(−u)K(\mathbf{u}) = K(-\mathbf{u})$
非负性： $K(u)≥0K(\mathbf{u}) \geq 0$
单峰性： 在原点达到最大值

实际应用考虑

带宽选择

h太小： 过拟合，估计过于粗糙
h太大： 欠拟合，过度平滑
自适应选择： 使用交叉验证或插值法则

K近邻密度估计的基本思想

核心理念

固定K，让V自适应

预先确定近邻数量K
让包含这K个近邻的区域体积V根据数据自动调整
密度高的地方V小，密度低的地方V大

构建过程详解

第一步：距离计算

计算查询点到所有样本点的距离

对于查询点 $x\mathbf{x}$ 和训练样本 ${x1,x2,...,xN}\{\mathbf{x}_1, \mathbf{x}_2, ..., \mathbf{x}_N\}$ ：

$di=∣∣x−xi∣∣d_i = ||\mathbf{x} - \mathbf{x}_i||$

常用距离度量：

欧几里得距离： $di=∑j=1D(xj−xi,j)2d_i = \sqrt{\sum_{j=1}^D (x_j - x_{i,j})^2}$
曼哈顿距离： $di=∑j=1D∣xj−xi,j∣d_i = \sum_{j=1}^D |x_j - x_{i,j}|$
闵可夫斯基距离： $di=(∑j=1D∣xj−xi,j∣p)1/pd_i = \left(\sum_{j=1}^D |x_j - x_{i,j}|^p\right)^{1/p}$

第二步：找到K个最近邻

排序并选择前K个

将所有距离 ${d_1, d_2, ..., d_N\}$ 排序
选择前K个最小的距离： $d(1)≤d(2)≤...≤d(K)d_{(1)} \leq d_{(2)} \leq ... \leq d_{(K)}$
记录对应的样本点： ${x(1),x(2),...,x(K)}\{\mathbf{x}_{(1)}, \mathbf{x}_{(2)}, ..., \mathbf{x}_{(K)}\}$