1328 Radar Installation

  
  

   
   Radar Installation
  
  

  
  


   
   
Time Limit: 1000MS
 
Memory Limit: 10000K
Total Submissions: 20456
 
Accepted: 4160
  
  
Description

  
  

   
   Assume the coasting is an infinite straight line. Land 
is in one side of coasting, sea in the other. Each small island is a point 
locating in the sea side. And any radar installation, locating on the coasting, 
can only cover d distance, so an island in the sea can be covered by a radius 
installation, if the distance between them is at most d. 
   
   

   
   
We use 
Cartesian coordinate system, defining the coasting is the x-axis. The sea side 
is above x-axis, and the land side below. Given the position of each island in 
the sea, and given the distance of the coverage of the radar installation, your 
task is to write a program to find the minimal number of radar installations to 
cover all the islands. Note that the position of an island is represented by its 
x-y coordinates. 
   
   


   
    
   
   
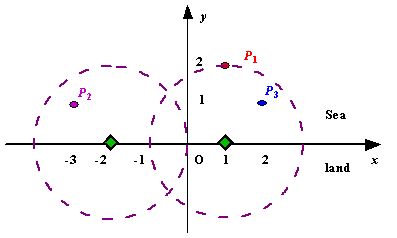
Figure A Sample Input of Radar 
Installations
   
   

  
  
Input

  
  

   
   The input consists of several test cases. The first 
line of each case contains two integers n (1<=n<=1000) and d, where n is 
the number of islands in the sea and d is the distance of coverage of the radar 
installation. This is followed by n lines each containing two integers 
representing the coordinate of the position of each island. Then a blank line 
follows to separate the cases. 
   
   

   
   
The input is terminated by a line 
containing pair of zeros 
  
  
Output

  
  

   
   For each test case output one line consisting of the 
test case number followed by the minimal number of radar installations needed. 
"-1" installation means no solution for that case.
  
  
Sample Input
3 2
1 2
-3 1
2 1

1 2
0 2

0 0

Sample Output
Case 1: 2
Case 2: 1

Source

  
  

   
   Beijing 2002
  
  

#include<iostream>
#include<cmath>
using namespace std;
struct coordinate//坐标结构体(x,y)
{
	int x,y;
}p[1001];
struct interval//区间结构体[a,b]
{
	double a;
	double b;
}b[1001];
int cmp_interval(const void *a,const void *b)
{
	interval *A = (interval*) a;
	interval *B = (interval*) b;
	return (*A).b > (*B).b ? 1: -1;
}//qsort的比较函数
double search(coordinate a,int d)
{
	double x;
	x = sqrt((double)(d*d - a.y*a.y)) + a.x;
	return x;
}//找出所给坐标对应的圆心允许范围
int main()
{
	int n,d,c = 0,r;//r = number of radar,c = case
	bool impossible;
	while(cin >> n >> d)
	{
		if(n == 0)break;
		++c;
		impossible = 0;
		r = 1;
		for(int i = 0;i < n;++i)
		{
			cin >> p[i].x >> p[i].y;
			if(abs(p[i].y) > d)
				impossible = 1;
			b[i].a = 2*p[i].x - search(p[i],d);
			b[i].b = search(p[i],d);
		}
		qsort(b,n,sizeof(b[0]),cmp_interval);//将区间按右边界从小到大排序
		if(impossible)
			cout <<"Case "<< c <<": " << -1 <<endl;
		else
		{
			int temp = 0;
			//贪心过程，策略是对包含区间取最右端的点，若左边界大于之前区间的右边界，则点数必须增加才能满足条件
			for(int i = 0;i < n;++i)
			{
				if(b[i].a > b[temp].b)
				{
					++r;
					temp = i;
				}
			}
			cout <<"Case "<< c <<": " << r << endl;
		}
	}
	return 0;
}