数据结构梳理（6） - 图

前言

这段时间偷懒了，上次二叉树写完之后，很长时间又没更新博客了，也没学啥东西，就一直咸鱼，所以今天赶紧脱离舒适区，继续把数据结构梳理完，目前为止，已经梳理了线性表、链表、栈、队列、二叉树，这次轮到图了，不出意外，图是数据结构系列的最后一篇，因为最基本的数据结构也就是这些，当然肯定还有其它各种各样的数据结构，实际开发中也会用到各种各样的高级容器，但是目前我的水平还不足够，对其它更高级的数据结构了解不多，等以后工作之后，再把后续高级的容器梳理出来吧，OK，不废话了，赶紧开始吧。

目录

1、图的结构、常见类型、表示方法
2、图的基本操作
2、基于邻接矩阵实现图
4、基于邻接表实现图

正文

1、图的结构、常见类型、重要概念、表示方法

首先来对图做一个基本的认识，从概念开始，官方给的图的概念如下：

图是一种数据元素间为多对多关系的数据结构，加上一组基本操作构成的抽象数据类型。

呃，读了一遍之后，发现还是很抽象，无法去形象化，没关系，我们通过概念只需要留个映像即可，从某种意义上来说，概念只是一种严格的定义，我们没有很大的必要去纠结它，当我们在使用图一段时间后，如果别人有一天问你，什么是图的时候，这时你已经对图有了一定的认知，但是你不知道怎么去完整准确的表述这个数据结构，这时候你再回过头看一下图的概念定义，你就明白概念存在的意义了。

为了方便快速建立对图的认知和学习，我还是以最常用也是最简单高效的办法，举一个图的例子，从这个例子中我们再来学习图，Ok，我这里就直接放出这个例子，然后针对这个例子，再来学习相关知识。

1.1 图的常见类型和结构

相信这里其实已经不用我来多赘述了，我们从图中可以一目了然，可以看到图一般分为两种类型，一种是无向图，一种是有向图，顾名思义，无向图中各节点连接的线是没有明确的方向的，而有向图中的就有方向，既然有方向就意味着这两个节点的关系是单向的，无方向就是双向的，至于这里提到的两个节点之间的“关系”具体是指什么，这个就要看具体业务场景了，比如要抽象出马路所表示的图结构，而马路上的普通车道自然就是无向的，单向车道就是有向的，所以其构建的图分别就是无向图和有向图。

接下来再来看看一个图的数据结构中主要包含哪些元素，对于一个图来说，一般的表示方法是使用两个元素来表示，一个是顶点，一个是边，也就是图由这两个元素来构成，这里的顶点其实就是包含数据元素值的节点，边其实就是这些节点间的关系。

了解了结构之后，我们再来看看两种类型的图的定义，来加深对图结构的理解，首先是无向图，它的定义如下：

无向图G=<V,E>,其中:
1.V是非空集合，称为顶点集。
2.E是V中元素构成的无序二元组的集合，称为边集。

要注意的就是第二点中“无序”两个字，其它的没啥了，在看完这个概念之后，再结合上面的图，怎么样，是不是对无向图有了一个清晰的认识，ok，然后再来看下有向图的定义：

有向图是一个二元组<V,E>，其中
1.V是非空集合，称为顶点集。
2.E是V×V的子集，称为弧集。

从概念中可以看到表述十分的严谨，既然是子集，那么同样的二元组<1,2>和<2,1>就是不同的，自然也就准确表述出了“有向”的效果。

1.2 图的其它重要概念

现在我们再来了解下关于图的一些其它专业名词，扩展下知识，这些概念可能在各个地方的表述都不一样，但是为了在我们深入学习图的时候，碰到这些词汇不至于一脸懵，所以我们还是有必要来学习的。

• 孤立点：V中不与E中任一条边关联的点称为D的孤立点
• 简单图：在无向图中，关联一对顶点的无向边如果多于1条，则称这些边为平行边，平行边的条数称为重数。在有向图中，关联一对顶点的有向边如果多于1条，并且这些边的始点与终点相同(也就是它们的的方向相同)，称这些边为平行边。含平行边的图称为多重图，既不含平行边也不含环的图称为简单图
• 完全无向图：设G是简单无向图，若G中任意节点都与其余节点邻接，则称G为完全无向图
• 完备图：图中任两个顶点a与b之间，恰有两条有向边(a，b)，及(b，a)，则称该有向图为完备图
• 基本图：把有向图D的每条边除去定向就得到一个相应的无向图G，称G为D的基本图，称D为G的定向图
• 强连通图：给定有向图G=(VE)，并且给定该图G中的任意两个结点u和v，如果结点u与结点v相互可达，即至少存在一条路径可以由结点u开始，到结点v终止，同时存在至少有一条路径可以由结点v开始，到结点u终止，那么就称该有向图G是强连通图
• 弱连通图：若至少有一对结点不满足单向连通，但去掉边的方向后从无向图的观点看是连通图，则D称为弱连通图
• 单向连通图：若每对结点至少有一个方向是连通的，则D称为单向连通图
• 强连通分支：有向图G的极大强连通子图称为该有向图的强连通分支
• 出度和入度：对有向图来说，以顶点为头的边的数目称为该顶点的入度，以顶点为尾（这里的尾指 指向顶点 的一端）的边的数目称为该顶点的出度，一个顶点的入度与出度之和称为该顶点的度。

我们没有必要一下子全部记下它们，只需要留有一个映像，当我们下次见到这些词汇的时候，能有个初步记忆，然后多回顾几次就自然而然记下来了。

1.3 图的表示方法

在了解了上面这么多枯燥的概念之后，我们再来学习一些比较有意思的知识，首先抛出一个问题，假设让你用数据的方式将一个图表示出来，你会怎么做呢，是不是感觉有点无从下手，毕竟图是一个抽象化的东西，而要使用数据量化的方式去表示还是很有难度的，当然你这时候可能有许多奇思妙想，可能你想出来的表达方式也很棒，不过我们还是来看看“走在我们前面的人”是怎么想的。

图的表示方法一般来说有两种：邻接矩阵和邻接表，下面我们来学习下这两个东西。

1.3.1 邻接矩阵表示法

首先学习邻接矩阵表示法，什么是邻接矩阵，其分为两部分：顶点集合和边集合。因此，有一个一维数组存放图中所有顶点数据，然后再用一个二维数组存放顶点间关系（边或弧）的数据，这个二维数组称为邻接矩阵。邻接矩阵又分为有向图邻接矩阵和无向图邻接矩阵。

看了上面相应的解释之后，我们还是拿上面的例子来看邻接矩阵表示法到底是如何表示一个图的，为了方便，再次贴上上面的例子图

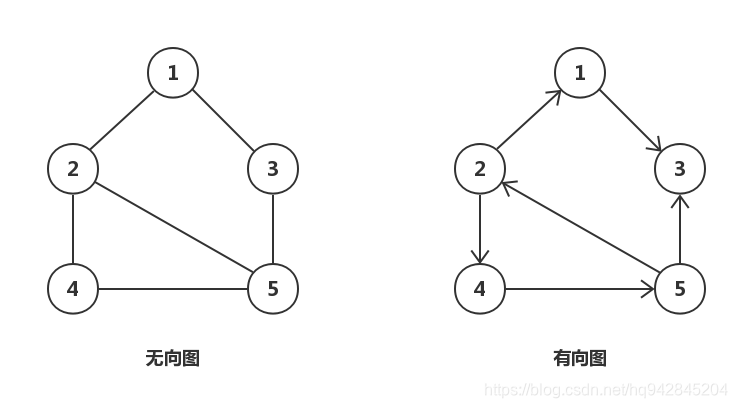
刚才说了，邻接矩阵表示法逻辑上分为两部分，一个一维数组用来存顶点元素，这个非常简单，声明一个一维数组存一下顶点即可，就不多说了，我们重点关注的就是另外一个二维数组，首先看左边的无向图，对这个图来说，二维数组的值应该是怎么样的呢，在这个图中，我们一共可以看到有五个顶点，然后我们将这五个顶点按照横向和纵向排列，形成一个类似坐标系的样子，如下

    1   2   3   4   5
    __________________
1 |
2 |
3 |
4 |
5 |

这样就形成了一个5*5的二维矩阵，然后矩阵中每个值相当于是对应的横纵坐标值的交叉点，这个交叉点的值怎么填呢，如果对应的横纵坐标值代表的顶点之间存在边，那么该值为1，如果不存在边，则为0，同时，对于对角线上的值，例如1和1的交叉点，也就是自己和自己的交叉点，因为这里没有环，所以就是0，最后，对于左边的无向图，其邻接矩阵如下

    1   2   3   4   5
    __________________
1 | 0   1   1   0   0                                     0   1   1   0   0
2 | 1   0   0   1   1       去掉无关的数,得到邻接矩阵         1   0   0   1   1
3 | 1   0   0   0   1            ====》》》                1   0   0   0   1 
4 | 0   1   0   0   1                                     0   1   0   0   1
5 | 0   1   1   1   0                                     0   1   1   1   0

我们可以发现对于无向图来说，其邻接矩阵有一个很明显的特点就是以对角线分割的“上三角”和“下三角”是对称的，那么这样可以带来什么效果呢，答案就是我们在存储的时候，可以只需要存储上三角或者下三角中的数据，而不用存储整个矩阵，这样就大大节约了空间开销。

ok，然后我们再来看看有向图