Python数学小实验（2）——观察几种典型分布

最新推荐文章于 2024-07-23 23:16:36 发布

MiaL

最新推荐文章于 2024-07-23 23:16:36 发布

阅读量535

点赞数 2

CC 4.0 BY-SA版权

分类专栏： Python数学小实验文章标签： rand randn

本文链接：https://blog.youkuaiyun.com/houhuipeng/article/details/90441898

Python数学小实验专栏收录该内容

6 篇文章

订阅专栏

本文通过Python进行数学实验，观察rand均匀分布和randn正态分布的特点。实验中还涉及指数分布的计算，展示了发生时间间隔的概率分布，并探讨了指数分布期望与方差不相等的现象。实验结果包括特定时间间隔出现的次数统计。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

Python数学小实验（2）——观察几种典型分布

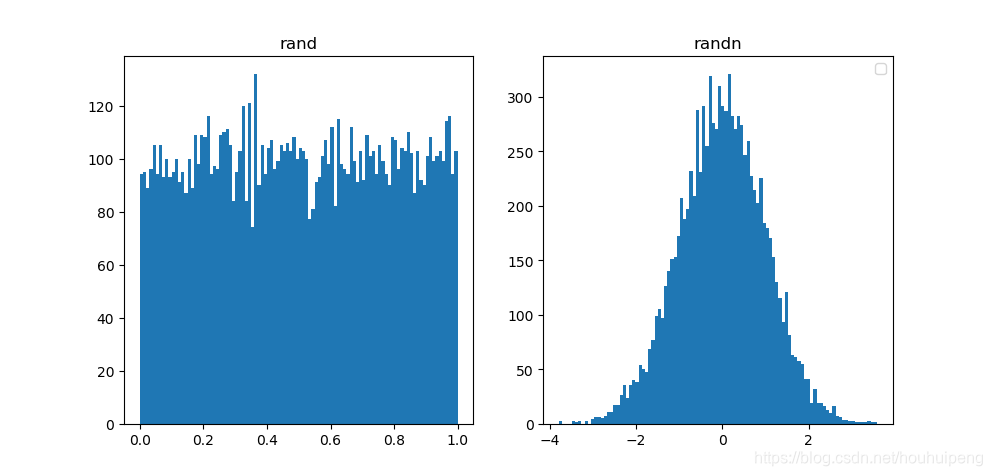
1、观察平均分布rand，正态分布randn

import numpy as np
import matplotlib.pyplot as plt

#from torch import random

y2 = np.random.randn(10000)
y1 = np.random.rand(10000)

f,(uniform,normal) =plt.subplots(ncols=2)

uniform.hist(y1,bins=100)
uniform.set_title('rand')
normal.hist(y2,bins=100)
normal.set_title('randn')

plt.show()

'''
def hist(
        x, bins=None, range=None, density=None, weights=None,
        cumulative=False, bottom=None, histtype='bar', align='mid',
        orientation='vertical', rwidth=None, log=False, color=None,
        label=None, stacked=False, normed=None, *, data=None,
        **kwargs)
'''

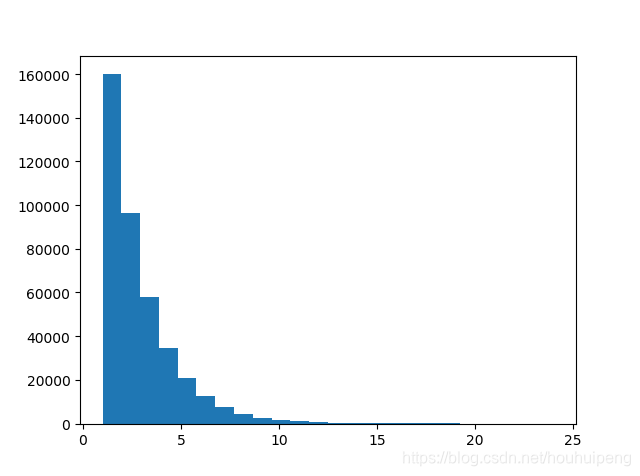
在这里插入图片描述

2、观察指数分布

问题描述：每分钟内，某时间发生的概率为0.6，过了1000000分钟，求发生的时间间隔的概率分布，求发生时间间隔大于20分钟的概率

import numpy as np 
import matplotlib.pyplot as plt
import matplotlib.mlab as mlab
from collections import Counter

time_stop = []
count = 0

for i in range(1,1000000):
    if (np.random.rand()) >0.6:
        count +=1
        if count== 1:
            time_start = i
        else:
            time_stop.append(i-time_start)
            time_start = i

print(np.mean(time_stop))  #输出均值（期望）
print(np.var(time_stop))  #输出方差
print(np.max(time_stop))  #输出最大值
print(Counter(time_stop))  #输出频数统计
plt.hist(time_stop,bins=np.max(time_stop),cumulative=False)
plt.show()

输出：

2.500974132346946
3.7563502939289948
26
Counter({1: 160223, 2: 95462, 3: 57655, 4: 34600, 5: 20799, 6: 12447, 7: 7325, 8: 4520, 9: 2756, 10: 1581, 11: 1028, 12: 590, 13: 352, 14: 199, 15: 133, 16: 66, 17: 41, 18: 29, 19: 19, 20: 9, 21: 5, 22: 2, 23: 1, 26: 1})

在这里插入图片描述
不解之处：
指数分布的期望和方差为什么会不相等？