Android电子书翻页效果

效果如图:

思路：计算出出各个顶点作为path路径连接 如图

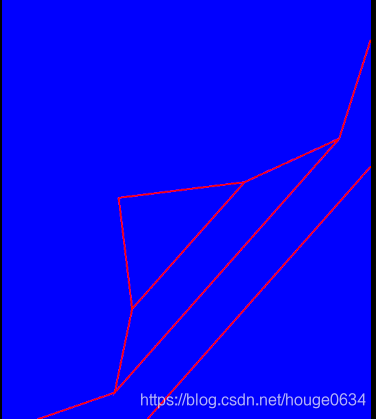
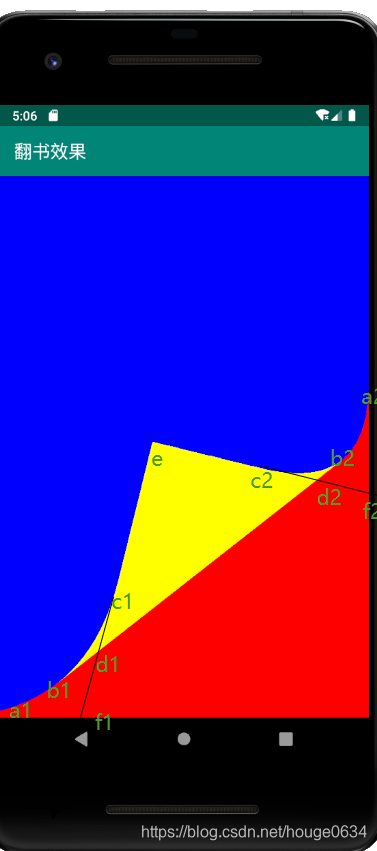
设屏幕右下角为原点O (view宽,view高),e为手指触摸屏幕的坐标，我们先算出点f1与f2的坐标

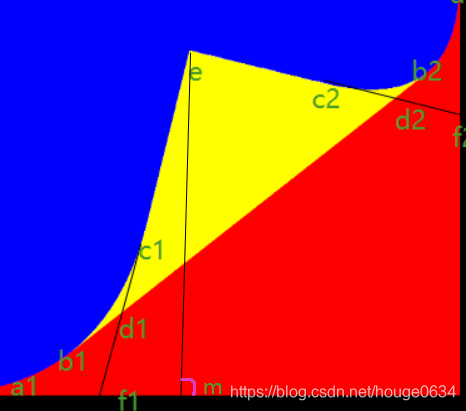
此处em代表两个点的线段距离,下文同上!
em=O.y-e.y(屏幕高度-e的Y坐标) ,Om=O.x-e.x; （.x代表某个点的x坐标）
可知方程 ef1²-f1m²=em²(勾股定理) ef1-f1m=Om; 因为em=Of1
=>(ef1+f1m)(ef1-f1m)=em²
=>(2ef1-Om）* Om=em²
=>ef1=(em²/Om+Om)/2;
=>f1.x=O.x-ef1

//pointF e 求f1坐标
float Om=getMeasuredWidth()-em.x;
float em=getMeasuredHeight()-em.y;
float ef1=(em*em/Om+Om)/2;
f1.x=getMeasuredWidth()-ef1;
f1.y=getMeasuredHeight();

根据方程可计算出 f1坐标 ,同理计算出f2坐标 。 注: (应该有更简单的计算公式,不过我高中和大学数学都忘了个差不多了。。。总之先计算f1,f2坐标)；

=======================================================
接下来计算a1和a2
我们这里让a1.x=f1.x-(O.x-f1.x)/2
float a1x=f1.x-(O.x-f1.x)/2;
PointF a1=new PointF(a1x,view高)
同理得a2

===========================================
接下来计算c1 和 c2
c1 实际上是 直线a1–a2 与 直线e–f1的交点:
通过直线函数求两条线的交点 如下:

 public PointF getIntersection(PointF pointF1,PointF pointF2, PointF pointF3,PointF pointF4){
   
   
        //第一条直线
        float x1 = pointF1.x, y1 = pointF1.y, x2 = pointF2.x, y2 =     				pointF2.y;
        float a = (y1 - y2) / (x1 - x2)