算法思想
二叉搜索树(又称二叉查找树或二叉排序树)BST树
二叉查找树
二叉查找树,也称二叉搜索树,或二叉排序树。其定义也比较简单,要么是一颗空树,要么就是具有如下性质的二叉树:
(1)若任意节点的左子树不空,则左子树上所有结点的值均小于它的根结点的值;
(2) 若任意节点的右子树不空,则右子树上所有结点的值均大于它的根结点的值;
(3) 任意节点的左、右子树也分别为二叉查找树;
(4) 没有键值相等的节点。
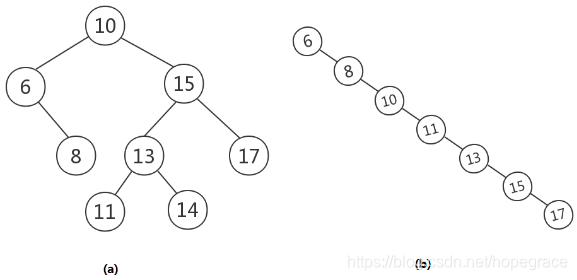
如上图所示,是不同形态的二叉查找树。二叉查找树是对要查找的数据进行生成树,左支的值小于右支的值。在查找的时候也是一样的思路,从根节点开始,比节点大进入右支,比节点小进入左支,直到查找到目标值。
二叉查找树的插入算法比较简单:空树,就首先生成根节点;不是空树就按照查找的算法,找到父节点,然后作为叶子节点插入,如果值已经存在就插入失败。
删除操作稍微复杂一点,有如下几种情况:
(1)如果删除的是叶节点,可以直接删除;
(2)如果被删除的元素有一个子节点,可以将子节点直接移到被删除元素的位置;
(3)如果有两个子节点,这时候就采用中序遍历,找到待删除的节点的后继节点,将其与待删除的节点互换,此时待删除节点的位置已经是叶子节点,可以直接删除。如下图:
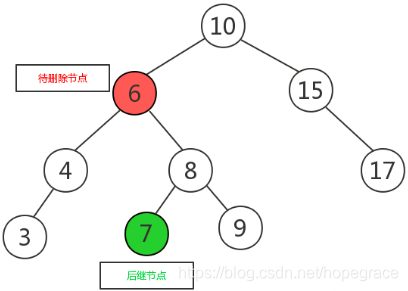
将待删除节点与后继节点互换,变成如下图所示:
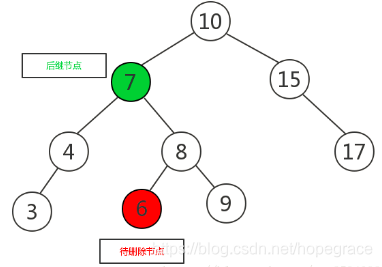
将待删除元素删除,如下图所示:
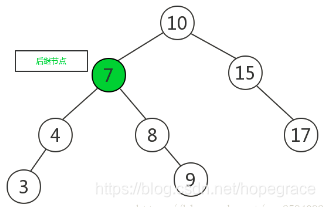
二叉查找树的性质总结:
a.二叉查找树还有一个性质,即对二叉查找树进行中序遍历,即可得到有序的数列。
b.二叉查找树的查询复杂度,和二分查找一样,插入和查找的时间复杂度均为 O(logn) ,但是在最坏的情况下仍然会有 O(n) 的时间复杂度。原因在于插入和删除元素的时候,树没有保持平衡(如上不同形态的二叉树图中的b)。
实现方法:
/****
* BinarySortTree.
*
****/
#include"stdafx.h"
#include <iostream>
#include<queue>
using namespace std;
// Data Structure Definition
typedef int KeyType;
typedef struct node
{
KeyType elem;
struct node* leftchild;
struct node* rightchild;
}BitNode, *BinTree;
//BinarySortTree
//insert operation
BinTree Insert_BinaryTree(BinTree bt, KeyType key)
{
if (bt == 0)
{
bt = new BitNode;
bt->elem = key;
bt->leftchild = 0;
bt->rightchild = 0;
return bt;
}
if (key < bt->elem)
bt->leftchild = Insert_BinaryTree(bt->leftchild, key);
else
bt->rightchild = Insert_BinaryTree(bt->rightchild, key);
return bt;
}
//Binary sort tree search algorithm
//BitNode* Search_BinaryTree(BinTree bt, KeyType key)
int Search_BinaryTree(BinTree bt, KeyType key)
{
if (bt == 0) return 0;
if (key == bt->elem) return 1;
if (key < bt->elem)
return Search_BinaryTree(bt->leftchild, key);
else
return Search_BinaryTree(bt->rightchild, key);
}
//another search algorithm
int Search_BinaryTree(BinTree bt, KeyType key, BitNode** p, BitNode** pf)
{
//pf is the pointer which point to the parent.
*p = bt;
*pf = 0;
while (*p != 0)
{
if (key == (*p)->elem) return 1;
if (key < (*p)->elem)
{
*pf = *p;
*p = (*p)->leftchild;
}
else
{
*pf = *p;
*p = (*p)->rightchild;
}
}
return 0;
}
//BinarySortTree
//Delete Operation
int Delete_BinaryTree(BinTree *bt, KeyType key)
{
BitNode* p = *bt;
BitNode* pf = 0; // pf is the parent of the p.
int findflag; //whether find or not.
if (*bt == 0) return 0; // tree is null.
findflag = Search_BinaryTree(*bt, key, &p, &pf);
if (findflag == 0) return 0; // no match.
//---------------------------------------------
//You need to delete a node that have no child.1.叶子节点
if (p->leftchild == 0 && p->rightchild == 0)
{
if (pf == 0) // delete the root node.
{
delete bt;
bt = 0;
return 1;
}
if (p == pf->leftchild)
pf->leftchild = 0;
else
pf->rightchild = 0;
delete p;
return 1;
}
//---------------------------------------------
//---------------------------------------------
//2You need to delete a node that have one child
if (p->leftchild == 0) // left child is null.
{
if (pf == 0) //delete the root node.
{
*bt = p->rightchild;
delete p;
return 1;
}
if (p == pf->leftchild)
pf->leftchild = p->rightchild;
else
pf->rightchild = p->rightchild;
delete p;
return 1;
}
if (p->rightchild == 0) // right child is null.
{
if (pf == 0) // delete the root node.
{
*bt = p->leftchild;
delete p;
return 1;
}
if (p == pf->leftchild)
pf->leftchild = p->leftchild;
else
pf->rightchild = p->leftchild;
delete p;
return 1;
}
//---------------------------------------------
//---------------------------------------------
//You need to delete a node that have two child
BitNode* prf = p;
BitNode* pr = p->rightchild;
while (pr->leftchild != 0)
{
prf = pr;
pr = pr->leftchild;
}
p->elem = pr->elem; //replace
if (prf == p)
prf->rightchild = pr->rightchild;
else
prf->leftchild = pr->rightchild;
delete pr;
return 1;
}
//print function
void printTree(BitNode* root)
{
queue<BitNode*> q;
q.push(root);
while (!q.empty())
{
auto p = q.front(); q.pop();
if (p)
{
cout << p->elem << " ";
q.push(p->leftchild);
q.push(p->rightchild);
}
}
cout << endl;
}
//test function
int main()
{
int a[10] = { 12, 52, 65, 84, 63, 14, 68, 69, 99,77 };
// initialization and creat the Binary Sort Tree.
BinTree bt = 0;
for (int i = 0; i < 10; i++)
{
bt = Insert_BinaryTree(bt, a[i]);
}
printTree(bt);
//search start.
cout << Search_BinaryTree(bt, 14) << endl;
cout << Search_BinaryTree(bt, 55) << endl;
//delete start.
cout << Delete_BinaryTree(&bt, 14) << endl;
//search 14 again.
cout << Search_BinaryTree(bt, 14) << endl;
system("pause");
return 0;
}
结果:
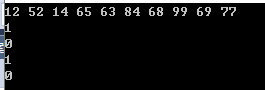







 本文详细介绍了二叉查找树的基本概念、性质及其实现方法,包括插入、查找和删除操作的具体步骤。通过示例展示了不同形态的二叉查找树及其在实际应用中的表现。
本文详细介绍了二叉查找树的基本概念、性质及其实现方法,包括插入、查找和删除操作的具体步骤。通过示例展示了不同形态的二叉查找树及其在实际应用中的表现。
















 263
263

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








