黄大叔学MPC系列之Lyapunov-based Nonlinear MPC
Lyapunov-based Nonlinear MPC
本文旨在复现Panagiotis D. Christofides教授在2012年发表的一篇论文,题为"Economic Model Predictive Control of Nonlinear Process Systems Using Lyapunov Techniques".
程序的运行环境是:
matlab2018b
加载了以下模块:
仿真对象
原论文采用的是一个典型的CSTR模型。在文中,原作者将其建立为一个以小时为时标的单位的模型。这样子做的一个好处是,在使用Casadi进行离散化的时候,可以降低参数的复杂度。
对象的微分方程模型如下:
C
A
d
t
=
F
V
(
C
A
0
−
C
A
)
−
k
0
e
−
E
R
T
C
A
2
\frac{C_A}{dt} = \frac{F}{V} (C_{A0}-C_{A})-k_{0}e^{\frac{-E}{RT}}C_A^2
dtCA=VF(CA0−CA)−k0eRT−ECA2
d
T
d
t
=
F
V
(
T
0
−
T
)
−
−
Δ
H
σ
C
p
k
0
e
−
E
R
T
C
A
2
+
Q
ρ
C
p
V
\frac{dT}{dt} = \frac{F}{V} (T_{0}-T)-\frac{-\Delta H}{\sigma C_{p}}k_{0}e^{\frac{-E}{RT}}C_A^2 + \frac{Q}{\rho C_{p}V}
dtdT=VF(T0−T)−σCp−ΔHk0eRT−ECA2+ρCpVQ
具体的模型参数如下表所示:

主函数
在主函数中,进行仿真对象参数的设置、非线性模型的构造、控制器的构造以及闭环仿真。
clc,clear,close all;
%%
mpc = import_mpctools();
%%
Para.T0 = 300; % k
Para.V = 1 ; % m^3
Para.k0 = 8.46e6; % m^3/(kmolhr)
Para.Cp = 0.231; % kJ/(kgK)
Para.roL= 1000; %kg/m^3
Para.Ts = 400; %400; % K
Para.Qs = 0; %kJ/hr
Para.F = 5; %m^3/hr
Para.E = 5e4; %kJ/kmol
Para.deltaH = -1.15e4; % kJ/kmol
Para.R = 8.314 ; %kJ/(kmolK)
Para.CAs = 2;%2; % kmol/m^3
Para.CA0s= 4; % kmol/m^3
%%
Delta = 0.01; % 0.01hr = 36s
Nx = 2;
Nu = 2;
Ny = Nx;
ode = @(x, u) CSTR_Continue(x, u, Para);
ode_rk4_casadi = mpc.getCasadiFunc(ode, [Nx, Nu], {'x', 'u'}, ...
{'ode_rk4'}, 'rk4', true(), 'Delta', Delta, 'M',10);
cstrsim = mpc.getCasadiIntegrator(ode, Delta, [Nx, Nu], ...
{'x', 'u'}, {'cstr'});
%% Steady-state values.
xs0 = [-0.0463116839087581 1.87265958853126]';
us = [0;0];
ode(xs0,us)
for i = 1:100
i
xs0 = full(cstrsim(xs0, us));
end
%%
Fnonlinear = ode_rk4_casadi;
l = mpc.getCasadiFunc(@(x,u) stagecost(x, u, Para), [Nx, Nu], {'x', 'u'}, {'l'});
h = mpc.getCasadiFunc(@(x) x, [Nx], {'x'}, {'h'});
Lyapunov_Constrains = mpc.getCasadiFunc(@(x,u) constrainst(x, u, Para), [Nx, Nu], {'x', 'u'}, {'e'});
%% Choose simulation time and preallocate everybody.
Nsim = 100;
x0 = xs0;
xcl = struct();
ucl = struct();
%% Build solvers for linear and nonlinear models.
Nt = 10;
ulb = [-3.5, -5e5]';
uub = [3.5, 5e5]';
lb = struct();
lb.u = repmat(ulb, 1, Nt);
ub = struct();
ub.u = repmat(uub, 1, Nt);
N = struct('x', Nx, 'u', Nu, 't', Nt, 'y', Ny);
kwargs = struct();
kwargs.N = N;
kwargs.l = l;
kwargs.lb = lb;
kwargs.ub = ub;
par = struct();
par.xsp = repmat(xs0, 1, Nt + 1);
par.usp = repmat(us, 1, Nt);
par.uprev = us;
kwargs.par = par;
%kwargs.e = Lyapunov_Constrains;
solvers = struct();%
solvers.nmpc = mpc.nmpc('f', Fnonlinear, 'e', Lyapunov_Constrains, '**', kwargs);
%% Simulate closed-loop control.
solvernames = fieldnames(solvers);
ub1 = [3.5*ones(64,1);-2.5*ones(2,1);-3.5*ones(104,1)];
lb1 = ub1;
for i = 1:length(solvernames)
s = solvernames{i};
solver = solvers.(s);
solver.saveguess(struct('x', par.xsp, 'u', par.usp));
solver.par.uprev = us;
xcl.(s) = NaN(Nx, Nsim + 1);
xcl.(s)(:,1) = x0;
ucl.(s) = NaN(Nu, Nsim);
for t = 1:Nsim
% 根据进料约束,人为更新设定u的上下界
for k = 1:Nt
solver.lb.u((k-1)*2+1) = lb1(t+k-1);
solver.ub.u((k-1)*2+1) = lb1(t+k-1);
end
% Set initial condition and solve.
solver.fixvar('x', 1, xcl.(s)(:,t));
solver.solve();
fprintf('%10s %3d: %s\n', s, t, solver.status);
if ~isequal(solver.status, 'Solve_Succeeded')
fprintf('*** Solver failed!\n');
break
end
solver.saveguess()
% Simulate system.
ucl.(s)(:,t) = solver.var.u(:,1);
xcl.(s)(:,t + 1) = full(cstrsim(xcl.(s)(:,t), ucl.(s)(:,t)));
Lyapunov_Constrains(xcl.(s)(:,t + 1),ucl.(s)(:,t))
% Update previous u.
solver.par.uprev = ucl.(s)(:,t);
end
end
%% Make a plot.
fig = figure();
% xsp = NaN(Nx, Nsim);
t = Delta*(0:Nsim);
plotargs = struct('fig', fig, 't', t);
mpc.mpcplot(xcl.nmpc, ucl.nmpc, 'legend', 'NMPC', 'color', 'g', ...
'**', plotargs); % 'xnames', {'c', 'T', 'h'}, 'unames', {'T_c', 'F'},
其中,需要为了满足文中Lyapunov的条件约束,需要对tk时刻的进行约束。为了充分利用mpctools自带的函数库,笔者对mpctools文件夹下的"pathconstraints.m"文件进行了修改。修改如下:
function pathcon = pathconstraints(Nt, e, vars, funcargs)
% pathcon = pathconstraints(Nt, e, vars, funcargs)
%
% Formulates nonlinear path constraints.
cons = cell(1, Nt);
for i = 1:Nt
if i == 1 ||i == 2
args = mpctools.getargs_(i, vars, funcargs);
try
cons{i} = e(args{:});
catch err
error('evaluating e(%s): %s', mpctools.row2str(funcargs), err.message);
end
if i == 1
Ne = size(cons{i}, 1);
end
else
cons{i} = zeros(Ne, 1);
end
end
% Package into struct.
pathcon = struct();
pathcon.con = cons;
pathcon.lb = -inf(Ne, Nt);
pathcon.ub = zeros(Ne, Nt);
end%function
模型函数
function [eq] = CSTR_Continue(x,u,Para)
%% Model parameters
T0 = Para.T0; % k
V = Para.V ; % m^3
k0 = Para.k0; % m^3/(kmolhr)
Cp = Para.Cp; % kJ/(kgK)
roL = Para.roL; %kg/m^3
Ts = Para.Ts; %400; % K
Qs = Para.Qs; %kJ/hr
F = Para.F; %m^3/hr
E = Para.E; %kJ/kmol
deltaH = Para.deltaH; % kJ/kmol
R = Para.R; %kJ/(kmolK)
CAs = Para.CAs;%2; % kmol/m^3
CA0s = Para.CA0s; % kmol/m^3
eq_1 = (F/V)*((u(1)+CA0s) - (x(1)+CAs)) - k0*exp(-E/(R*(x(2)+Ts)))*(x(1)+CAs)^2;%注意这里删去了^2
eq_2 = (F/V)*(- x(2)) + ((-deltaH)/(roL*Cp))*k0*exp(-E/(R*(x(2)+Ts)))*(x(1)+CAs)^2 + F/V*(T0-Ts) + (u(2)+Qs)/(roL*Cp*V);
eq = [eq_1;eq_2];
目标函数
function cost = stagecost(x, u, Para)
%% Model parameters
T0 = Para.T0; % k
V = Para.V ; % m^3
k0 = Para.k0; % m^3/(kmolhr)
Cp = Para.Cp; % kJ/(kgK)
roL = Para.roL; %kg/m^3
Ts = Para.Ts; %400; % K
Qs = Para.Qs; %kJ/hr
F = Para.F; %m^3/hr
E = Para.E; %kJ/kmol
deltaH = Para.deltaH; % kJ/kmol
R = Para.R; %kJ/(kmolK)
CAs = Para.CAs;%2; % kmol/m^3
CA0s = Para.CA0s; % kmol/m^3
cost = k0*exp(-E/(R*(x(2)+Ts)))*(x(1)+CAs)^2;
cost = - cost;
end%function
Lyapunov 约束函数
function e =constrainst(x,u,Para)
gamma = 9.53; %这个值是论文中取的,也可以自己通过试凑得到
%% Model parameters
T0 = Para.T0; % k
V = Para.V ; % m^3
k0 = Para.k0; % m^3/(kmolhr)
Cp = Para.Cp; % kJ/(kgK)
roL = Para.roL; %kg/m^3
Ts = Para.Ts; %400; % K
Qs = Para.Qs; %kJ/hr
F = Para.F; %m^3/hr
E = Para.E; %kJ/kmol
deltaH = Para.deltaH; % kJ/kmol
R = Para.R; %kJ/(kmolK)
CAs = Para.CAs;%2; % kmol/m^3
CA0s = Para.CA0s; % kmol/m^3
%%
x1 = x(1);
x2 = x(2);
u1 = u(1);
u2 = u(2);
%%
eq_2 = (F/V)*(- x(2)) + ((-deltaH)/(roL*Cp))*k0*exp(-E/(R*(x(2)+Ts)))*(x(1)+CAs)^2 + F/V*(T0-Ts) + (u(2)+Qs)/(roL*Cp*V);
e = 2*(x2-30)*eq_2 + gamma*(x2-30)^2;
% e2 =
end
仿真的最后结果如下:
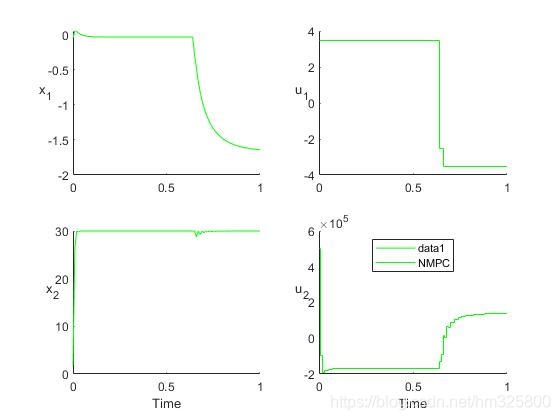
以下是论文中的结果图:
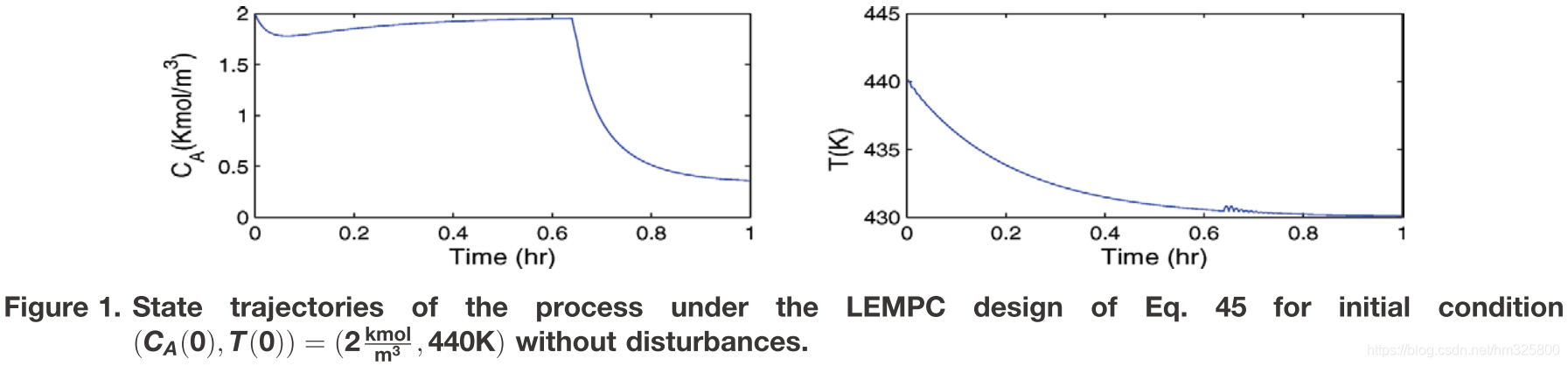
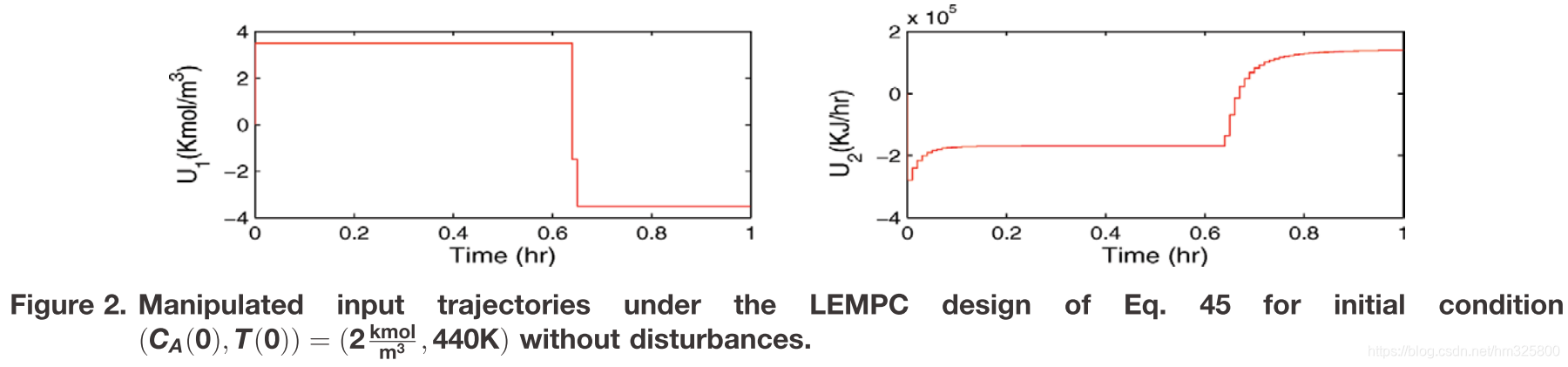
不同之处在于,仿真的起始点不同。





 本文复现了Christofides教授关于经济模型预测控制的研究,利用Matlab和Casadi工具箱实现CSTR模型的非线性MPC,强调Lyapunov稳定性的应用。
本文复现了Christofides教授关于经济模型预测控制的研究,利用Matlab和Casadi工具箱实现CSTR模型的非线性MPC,强调Lyapunov稳定性的应用。

















 4114
4114

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








