Leetcode 5270、网格中的最小路径代价

Leetcode 5270、网格中的最小路径代价

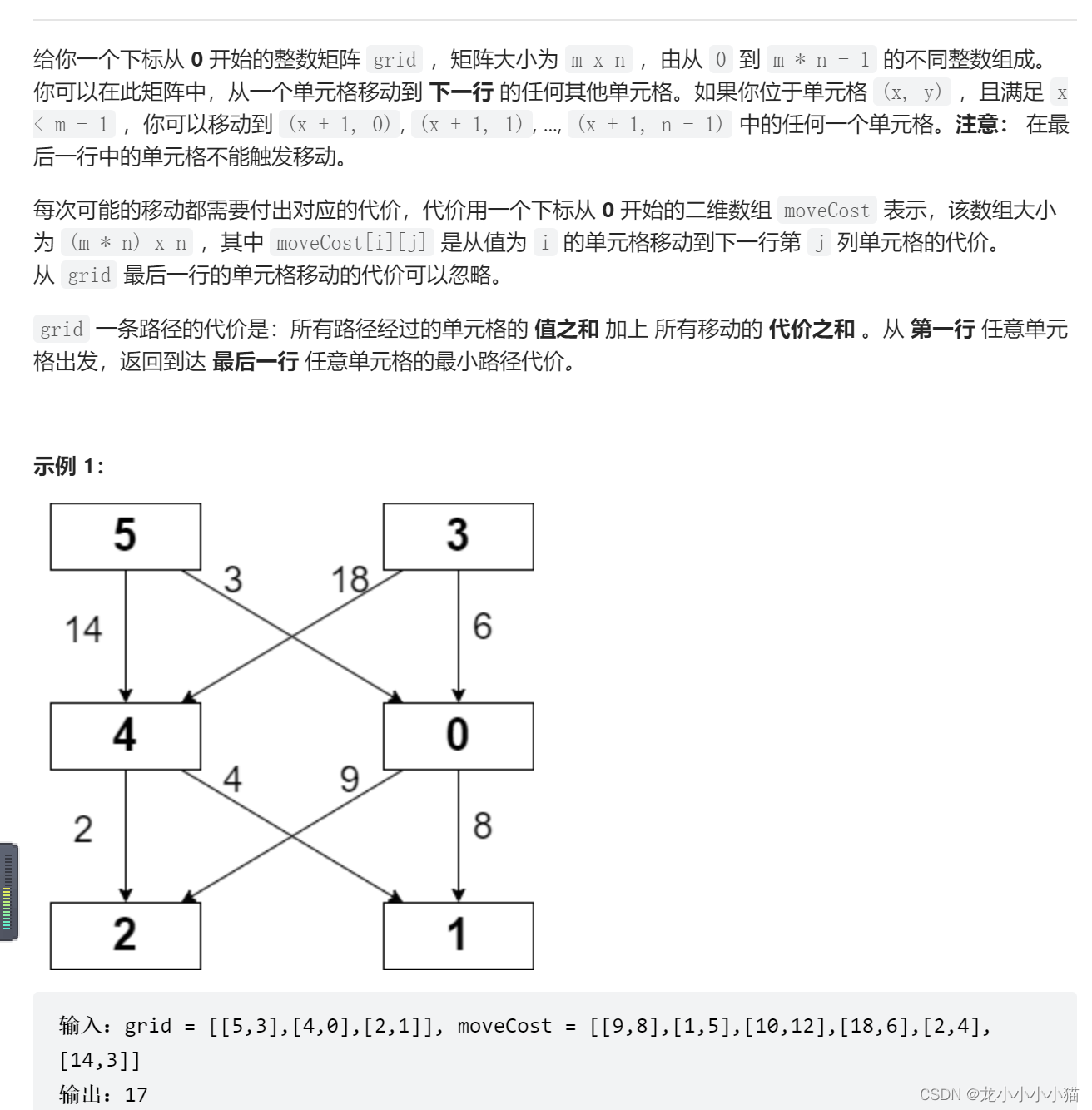
使用动态规划进行解题，dp数组存储中间结果，当前层的结果只依赖上一层的值。这里的dp数组是二维数组，其实可以只使用一维数组存储上一层的值就可以，减少占用的空间。

class Solution {
    public int minPathCost(int[][] grid, int[][] moveCost) {
        int m = grid.length, n = grid[0].length;
        int[][] dp = new int[m][n]; // 从上一个位置传递过来到现在的最小的值
        for(int i = 0; i < m; i++) {
            Arrays.fill(dp[i], Integer.MAX_VALUE);
        }
        // 初始化
        for(int i = 0; i < n; i++) {
            dp[0][i] = grid[0][i];
        }

        /**
            i代表是当遍历的层数
            k代表当前层的第k个位置，每一次找一个位置
            j代表上一层的每个元素的下标

            当前层等于上一层的值+路程值的最小值，最后加上当前层的值。
         */
        for(int i = 1; i < m; i++) {
            for(int k = 0; k < n; k++) {
                for(int j = 0; j < n; j++) {
                    int move = moveCost[grid[i - 1][j]][k];
                    dp[i][k] = Math.min(dp[i][k], dp[i - 1][j] + move);
                }
                dp[i][k] += grid[i][k];
            }
        }

        // 最后返回最后一层的最小值。
        return Arrays.stream(dp[m - 1]).min().getAsInt();
    }
}