高中数学之向量外积的运用

向量积，数学中又称外积、叉积，物理中称矢积、叉乘，是一种在向量空间中向量的二元运算。与点积不同，它的运算结果是一个向量而不是一个标量。并且两个向量的叉积与这两个向量和垂直。其应用十分广泛，通常应用于物理学光学和计算机图形学中。
如图，这是 $(2,4)\times (3,0)=-12$ ，我们得到了一个实数 $-12$ ，而其绝对值为平行四边形面积。

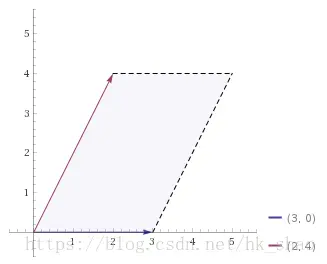
如图，这是 $(1,0,0)\times (2,4,0)=(0,0,4)$ ，我们得到了一个垂直与已知两向量的法向量，且其模长为平行四边形面积。

运算定理

$\vec{a},b$ 均为向量，$\theta$ 为 $\vec{a},b$ 的夹角

1，$\vec{a}\times \vec{b}=|\vec{a}|\times |\vec{b}|sin\theta$

2，$\vec{a}\times \vec{b}=(l,m,n)\times (o,p,q)$