jupyter下的python基本使用和信号处理编程

最新推荐文章于 2025-02-20 23:17:26 发布

刘晶123

最新推荐文章于 2025-02-20 23:17:26 发布

阅读量1.7k

点赞数

分类专栏： centos

本文链接：https://blog.youkuaiyun.com/hjw1314kl/article/details/103245120

版权

centos 专栏收录该内容

21 篇文章

订阅专栏

jupyter下的python基本使用和信号处理编程

简介：

jupyter notebook是一种 Web 应用，能让用户将说明文本、数学方程、代码和可视化内容全部组合到一个易于共享的文档中。它可以直接在代码旁写出叙述性文档，而不是另外编写单独的文档。也就是它可以能将代码、文档等这一切集中到一处，让用户一目了然。

实验环境：

腾讯云服务器centos7

一、安装jupyter notebook

可以参考我的另一篇博客：https://blog.youkuaiyun.com/hjw1314kl/article/details/102233752

二、jupyter notebook的简单使用

首先你需要启动jupyter notebook，在命令行输入：jupyter lab --allow-root

[root@VM_0_17_centos ~]# jupyter lab --allow-root
[W 19:19:19.530 LabApp] WARNING: The notebook server is listening on all IP addresses and not using encryption. This is not recommended.
............................
............................

然后在网页中输入http://139.199.6.165:8888,我使用的是8888端口。

在这里插入图片描述
这图片是谷歌自动翻译了的，所以不是很准确

我们可以修改jupyter的工作目录，也可以保持原样不变，如果修改的话，要保证这一目录已存在，我使用的是默认目录，所以是打开是root目录。在命令行创建一个文件夹用于存放jupyter的文件，我创建的是python文件夹。右边的图标点击就可以编辑对应文件了。

三、jupyter运行环境的配置-----python基本使用和信号处理编程

jupyter notebook本质上是一个web应用程序，我们可以在上面书写代码，但是代码本身的运行环境是需要自己安装的，没有运行环境，即使是在jupyter notebook里面书写的代码怡然没有办法运行。因为代码本身，web应用程序是不认识的。

但是我们安装了anaconda3,他会默认安装jupyter和python运行环境。

第一个python3 ，表示的就是默认的python3 kernel，它是随着anaconda一起安装的；点击就可以自动创建文件开始编写python。

Text File ,表示的是新建一个文本文件

Terminal ，表示的是在浏览器中新建一个用户终端，即类似于cmd的shell。

jupyter的简单编写程序

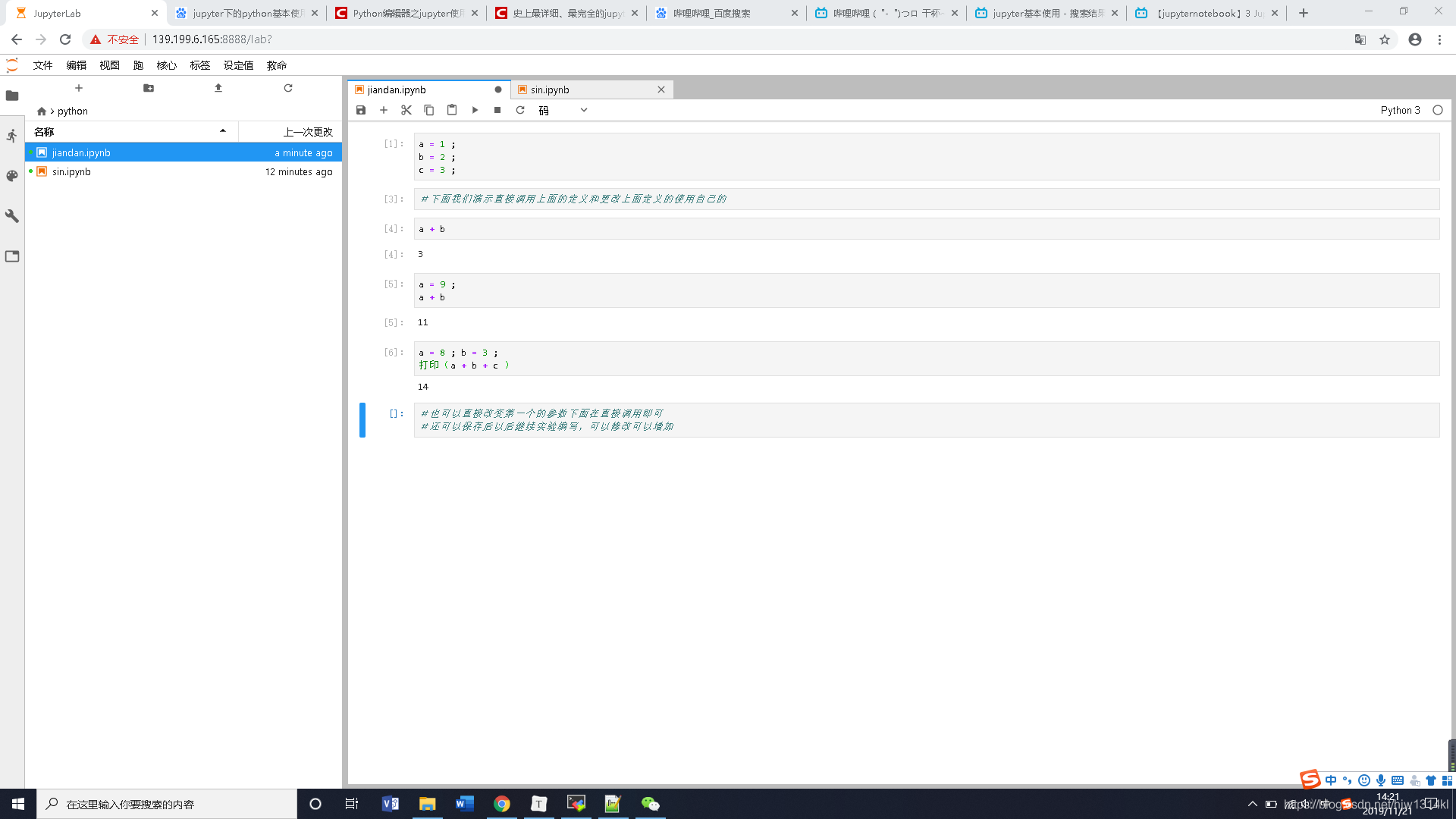
在这里插入图片描述

jupyter调用python包编辑三角函数

下面演示一下调用包就行简单的三角函数运算并输出时间，因为使用anaconda含有大量的python的软件包和环境，所以直接调用就可以不用安装包：

里面的数据是可以直接修改然后再运行也可以，很方便实验使用。
在这里插入图片描述

jupyter调用python包进行简单fft变换

这里运行时单个模块单个模块的运行，上面的运行了下面的才能调用，而且这样单模块操作很容易找出错误。

import matplotlib.pyplot as plt
import numpy as np
from matplotlib.pylab import mpl

mpl.rcParams['font.sans-serif'] = ['SimHei']   #显示中文
mpl.rcParams['axes.unicode_minus']=False       #显示负号

Fs = 150.0;                 # 采样率
Ts = 1.0/Fs;                # 采样区间
t = np.arange(0,1,Ts)       # 时间矢量，这里Ts也是步长
#range返回从0到1构成的list，而arange返回一个array对象

fs = 25;                    # frequency of the signal信号频率
y = np.sin(2*np.pi*fs*t)

n = len(y)                  # 信号长度
k = np.arange(n)            #采样点数的等差数列k
T = n/Fs                    #共有多少个周期T
frq = k/T                   # two sides frequency range两侧频率范围
frq1 = frq[range(int(n/2))] # #由于对称性，取一半区间

YY = np.fft.fft(y)          # 未归一化
Y = np.fft.fft(y)/n         #  归一化
Y1 = Y[range(int(n/2))]
##这里注释掉，是想演示在下面调用上面的数据............................
#fig, ax = plt.subplots(4, 1)

#ax[0].plot(t,y)
#ax[0].set_xlabel('Time')
#ax[0].set_ylabel('振幅')

#ax[1].plot(frq,abs(YY),'r') #绘制频谱
#ax[1].set_xlabel('Freq (Hz)')
#ax[1].set_ylabel('|Y(freq)|')

#ax[2].plot(frq,abs(Y),'g')  # plotting the spectrum
#ax[2].set_xlabel('Freq (Hz)')
#ax[2].set_ylabel('|Y(freq)|')

#ax[3].plot(frq1,abs(Y1),'b') # plotting the spectrum
#ax[3].set_xlabel('Freq (Hz)')
#ax[3].set_ylabel('|Y(freq)|')

#plt.show()

fig, ax = plt.subplots(4, 1)

ax[0].plot(t,y)
ax[0].set_xlabel('Time')
ax[0].set_ylabel('振幅')

ax[1].plot(frq,abs(YY),'r') #绘制频谱
ax[1].set_xlabel('Freq (Hz)')
ax[1].set_ylabel('|Y(freq)|')

ax[2].plot(frq,abs(Y),'g')  # plotting the spectrum
ax[2].set_xlabel('Freq (Hz)')
ax[2].set_ylabel('|Y(freq)|')

ax[3].plot(frq1,abs(Y1),'b') # plotting the spectrum
ax[3].set_xlabel('Freq (Hz)')
ax[3].set_ylabel('|Y(freq)|')

plt.show()

运行结果：
在这里插入图片描述

jupyter调用python包进行语音处理

import wave
import matplotlib.pyplot as plt
from scipy.io import wavfile
import numpy as np
# 打开WAV音频
f = wave.open(r"/root/python/C2_1_y_1.wav", "rb")
# 读取格式信息
# (声道数、量化位数、采样频率、采样点数、压缩类型、压缩类型的描述)
# (nchannels, sampwidth, framerate, nframes, comptype, compname)
params = f.getparams()
nchannels, sampwidth, framerate, nframes = params[:4]
print(nchannels, sampwidth, framerate, nframes) 
# 读取nframes个数据，返回字符串格式
str_data = f.readframes(nframes)
#将字符串转换为数组，得到一维的short类型的数组
wave_data = np.frombuffer(str_data, dtype=np.short)
# 赋值的归一化
wave_data = wave_data*1.0/(max(abs(wave_data))
# 最后通过采样点数和取样频率计算出每个取样的时间
time = np.arange(0, nframes) * (1.0 / framerate)
#绘画原始语音图像
plt.figure()
plt.plot(time, wave_data,color="red")
plt.xlabel("time (seconds)") #x轴坐标
plt.ylabel("Amplitude")   #y轴坐标
plt.title("Left channel")  #标题
plt.show()

# 应用傅里叶变换
fft_signal = np.fft.fft(wave_data)   #进行傅里叶变换
fft_signal = abs(fft_signal)   # 取复数的绝对值，即复数的模(双边频谱)
# 建立时间轴
Freq = np.arange(0, len(fft_signal))  
# 绘制语音信号的
plt.figure()
plt.plot(Freq, fft_signal, color='red')
plt.xlabel('Freq (in kHz)')
plt.ylabel('Amplitude')
plt.show()

运行结果：
在这里插入图片描述

在上面的基础上还可以继续在jupyter调用python包进行语音的分帧处理及加窗处理

wlen为帧长，inc为帧移，重叠部分为overlap，overlap=wlen - inc

信号帧数为：
$fn=\left( N−overlap \right) /inc=\left( N−wlen \right) /inc+1$
N为语音数据长度。

每一帧的起始点的位置为：
$startindex=\left( 0:\left( fn−1 \right) \right) *inc+1$

wlen=512  #帧长
inc=128   #帧移      
time = np.arange(0, wlen) * (1.0 / framerate) #一帧的时间
signal_length=len(wave_data) #信号总长度
if signal_length<=wlen: #若信号长度小于一个帧的长度，则帧数定义为1
        nf=1
else:                 #否则，计算帧的总长度
        nf=int(np.ceil((1.0*signal_length-wlen)/inc)+1)
        
pad_length=int((nf-1)*inc+wlen) #所有帧加起来总的铺平后的长度
zeros=np.zeros((pad_length-signal_length,)) #不够的长度使用0填补，类似于FFT中的扩充数组操作
pad_signal=np.concatenate((wave_data,zeros)) #填补后的信号记为pad_signal
indices=np.tile(np.arange(0,wlen),(nf,1))+np.tile(np.arange(0,nf*inc,inc),(wlen,1)).T  #相当于对所有帧的时间点进行抽取，得到nf*nw长度的矩阵
indices=np.array(indices,dtype=np.int32) #将indices转化为矩阵
frames=pad_signal[indices] #得到帧信号
a=frames[30:31]
plt.figure()
plt.plot(time,a[0],c="g")
plt.xlabel('time')
plt.ylabel('changdu')
plt.show()

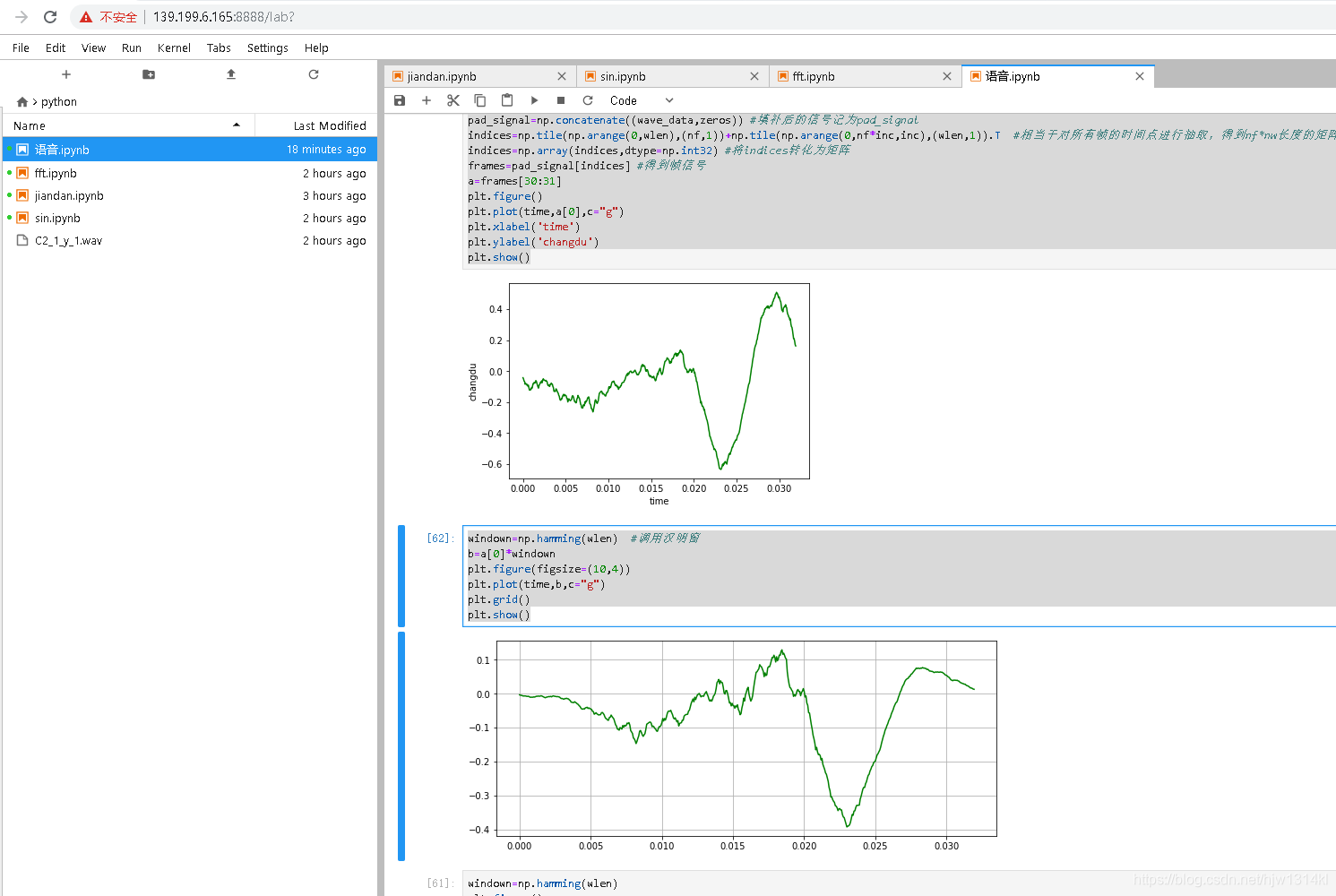
windown=np.hamming(wlen)  #调用汉明窗
b=a[0]*windown
plt.figure()
plt.plot(time,b,c="g")
plt.grid()
plt.show()

运行结果：
在这里插入图片描述

在前面基础上绘制语谱图：

plt.specgram(wave_data,Fs = framerate,scale_by_freq=True,sides='default')    
plt.ylabel('Frequency')
plt.xlabel('Time(s)')
plt.title('Spectrogram')

运行结果：
在这里插入图片描述

在前面基础上提取mfcc：

通过python_speech_features提取mfcc:

from scipy.io import wavfile
from python_speech_features import mfcc, logfbank

mfcc_features = mfcc(wave_data)
filterbank_features = logfbank(wave_data)
print('\nMFCC:\n窗口数 =', mfcc_features.shape[0])
print('每个特征的长度 =', mfcc_features.shape[1])
print('\nFilter bank:\n窗口数 =', filterbank_features.shape[0])
print('每个特征的长度 =', filterbank_features.shape[1])
# 画出特征图，将MFCC可视化。转置矩阵，使得时域是水平的
mfcc_features = mfcc_features.T
plt.matshow(mfcc_features)
plt.title('MFCC')
# 将滤波器组特征可视化。转置矩阵，使得时域是水平的
filterbank_features = filterbank_features.T
plt.matshow(filterbank_features)
plt.title('Filter bank')
plt.show()