文章目录
1-3. 概念题

4. 如何限制空间

1.约束版本
对于线性回归问题,限定参数向量
w的大小,即||w||₂ ≤ c。这里c是一个预先设定的常数,用于限制w的长度。这个约束条件直接对参数向量的长度进行了限制,确保其不会过大或过小。
2.无约束版本min ( 1 2 N ∣ ∣ X w − y ∣ ∣ 2 2 + λ 2 ∣ ∣ w ∣ ∣ 2 2 ) \min(\frac{1}{2N}||Xw - y||_2^2+\frac{\lambda}{2}||w||_2^2) min(2N1∣∣Xw−y∣∣22+2λ∣∣w∣∣22)
N是样本数量,X是输入数据矩阵,w是参数向量,y是目标值向量。这个目标函数由两部分组成:第一部分是均方误差项,表示模型对数据的拟合程度;第二部分是正则化项,通过惩罚参数向量w的长度来防止过拟合。参数λ用于控制正则化的强度。
通过调整λ的值,可以在拟合数据和限制参数大小之间进行权衡。
- 当
λ较大时,正则化项的作用更强,参数向量w会更趋向于零向量,从而防止过拟合;- 当
λ较小时,正则化项的作用较弱,模型更注重拟合数据。例如,在实际应用中,可以通过交叉验证等方法来选择合适的
λ值,以获得最佳的模型性能。
5. 梯度下降的计算

6. 随机梯度下降

- 批较小时的影响
- 随机梯度噪声大: 批大小很小时,每次用于计算梯度的样本少,导致计算出的随机梯度与真实梯度偏差大,噪声大。例如在图像分类任务中,小批大小可能使梯度在不同方向剧烈波动,影响模型向最优解前进。
- 不易收敛: 由于随机梯度噪声大,模型参数更新不稳定,难以收敛到较好的解。在回归问题中,模型可能在最优解附近振荡,且小批大小可能使模型陷入局部最优解。
- 批较大时的影响
- 运行速度慢:批大小较大时,每次参与梯度计算的样本多,虽然能减少随机梯度噪声,但会增加计算量和内存占用,导致训练速度变慢。
- 可能陷入局部最优:较大的批大小可能使模型参数更新过于“平滑”,缺乏对不同局部区域的探索能力,容易陷入局部最优解,错过全局最优解。
总之,在随机梯度下降中,选择合适的批大小很重要,需要综合考虑数据集大小、硬件资源和模型复杂度等因素,平衡随机梯度噪声和训练效率,以获得更好的训练效果。
7. Softmax计算

u u u的含义: u u u是一个属于 k k k维实数空间( u ∈ R k u\in\mathbb{R}^{k} u∈Rk)的向量。这意味着 u u u有 k k k个分量,每个分量都是一个实数。
y y y的含义: y y y是向量 u u u经过Softmax变换后得到的向量。
- Softmax函数常用于多分类问题中,它将一个 k k k维的实数向量转换为一个 k k k维的概率分布向量。具体来说,对于向量 u = ( u 1 , u 2 , ⋯ , u k ) u=(u_{1},u_{2},\cdots,u_{k}) u=(u1,u2,⋯,uk),经过Softmax变换后得到的向量 y = ( y 1 , y 2 , ⋯ , y k ) y=(y_{1},y_{2},\cdots,y_{k}) y=(y1,y2,⋯,yk),其中:
y i = e u i ∑ j = 1 k e u j y_{i}=\frac{e^{u_{i}}}{\sum_{j = 1}^{k}e^{u_{j}}} yi=∑j=1keujeui- 这里的 y i y_{i} yi表示向量 y y y中的第 i i i个元素,它代表了输入向量 u u u对应的第 i i i个类别上的概率。
注意:求导时,对求和的导数
8. 岭回归思想

岭回归的基本思想如下:
一、问题背景
在传统的线性回归中,通常使用最小二乘法来求解模型参数,其目标是最小化损失函数 1 2 N ∣ ∣ X w − y ∣ ∣ 2 2 \frac{1}{2N}||Xw - y||_2^2 2N1∣∣Xw−y∣∣22,其中(X)是输入数据矩阵,(w)是模型参数向量,(y)是目标值向量。然而,在实际应用中,当数据特征较多或者存在相关性时,普通的线性回归容易出现过拟合的问题。
二、基本思想引入
为了解决过拟合问题,岭回归在普通线性回归的损失函数基础上引入了对参数向量(w)的约束。具体来说,岭回归希望同时限定 ∣ ∣ w ∣ ∣ 2 2 ||w||_2^2 ∣∣w∣∣22(即(w)的长度平方)的大小,要求(w)的长度满足 ∣ ∣ w ∣ ∣ 2 2 ≤ c ||w||_2^2\leq c ∣∣w∣∣22≤c,其中(c)是一个预先设定的常数。这样做的直觉是,通过限制参数向量的长度,可以有效地缩小解空间的大小。
三、作用及意义
- 解决过拟合:限制解空间的大小有助于防止模型过度拟合训练数据。岭回归通过限制参数向量的长度,使得模型在选择特征时更加谨慎,从而提高了模型的泛化能力。
- 稳定性提升:在数据存在噪声或不确定性的情况下,岭回归可以减少参数估计的方差,使得模型对不同的数据集具有更好的鲁棒性。
总之,岭回归的基本思想是在普通线性回归的基础上,通过引入对参数向量长度的约束,来解决过拟合问题并提高模型的稳定性和泛化能力。
9. 套索回归基本思想

通过这样的约束,套索回归能够促使模型在众多特征中选择出最重要的一部分特征,将不重要的特征对应的参数设置为零,从而实现特征选择和提高模型的解释性,同时也有助于防止过拟合,提高模型的泛化能力。
10. Sigmoid函数

11. 岭回归使用的范数

12. 计算回归方程

参考:《人工智能基础-姚期智》







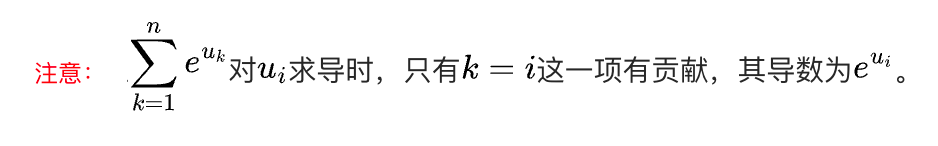



















 589
589

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










