文章目录
一. 监督、无监督、半监督学习
1. 监督学习
监督学习分为回归问题(=函数拟合)和分类问题
分类模型有:决策树、逻辑回归、支持向量机
回归问题:等价于函数拟合,即选择一个函数可以很好地拟合已知数据且能正确预测未知数据。回归正是用于捕捉输入到输出之间的函数映射关系。
2. 无监督学习
无监督学习中,训练数据不包含标签,算法需要找出数据中的结构和模式。
聚类是无监督学习中的一种算法:
聚类是将数据集中的样本根据相似性分组,使得同一组内相似度高、不同组样本相似度低。常见聚类算法:k-means、层次聚类、DBSCAN。
2.1. k-means算法:处理球形簇
目标:将数据集中的n个样本划分为k个簇,使得簇内的样本尽可能相似,而簇间的样本尽可能不同。
k-means算法的基本步骤:
算法优缺点:
优点:简单、高效、且容易实现
局限性:
- 对初始簇中心的选择敏感,可能造成局部最优解。
- 需要事先指定簇的数量k,这在实际应用中可能并不容易确定;
- 对于非球形的簇或者大小差异较大的簇,聚类效果可能不佳;
- 对噪声和异常点敏感。
为了解决这些问题,研究者们提出了一些改进的算法,如K-means++用于更好的初始簇中心选择,以及使用不同的距离度量和聚类评估指标来提高聚类的质量。
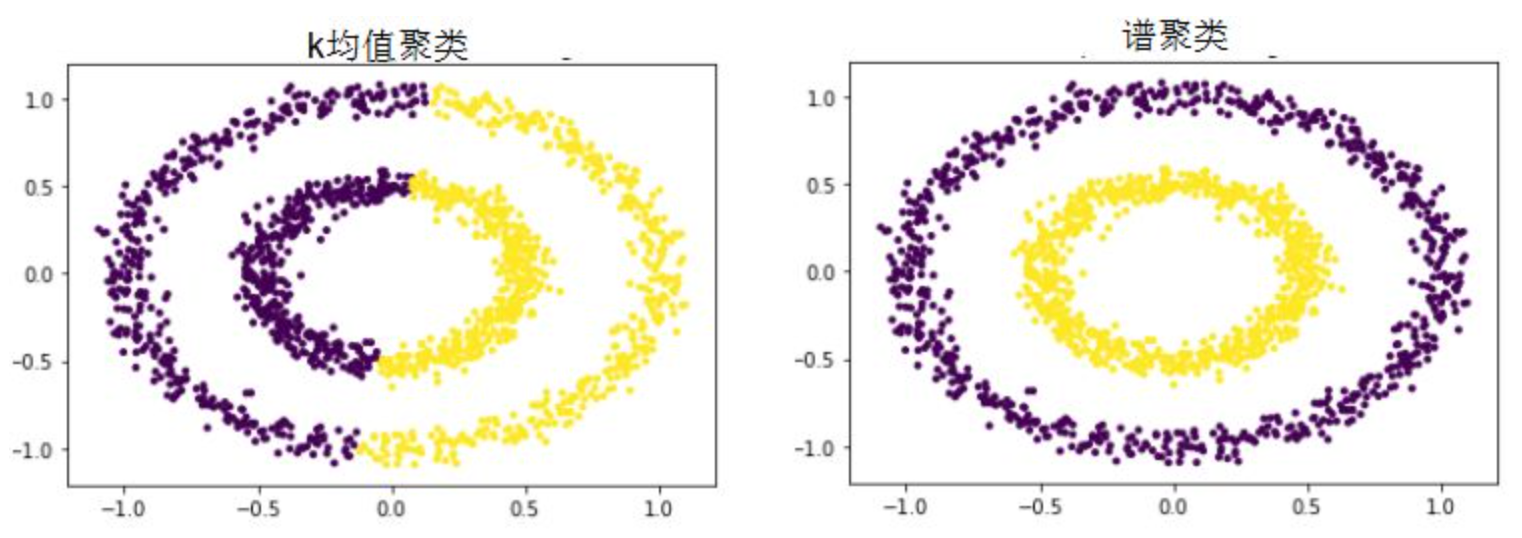
2.2. 谱聚类:处理非球形簇和高维数据
谱聚类(Spectral Clustering)是一种基于图论的聚类算法,它将数据集中的每个样本视为图中的一个顶点,样本间的相似度则转化为连接这些顶点的边的权重。
谱聚类的核心思想是通过图的切割方法,将图分割成若干个子图,使得每个子图内部的边权重和尽可能大,而子图之间的边权重和尽可能小,从而实现聚类的目的。
谱聚类的基本步骤包括:
| 步骤 | 描述 | |
|---|---|---|
| 1.构建相似度矩阵 | 首先,需要构建一个相似度矩阵来表示数据点之间的相似程度。这个矩阵可以是基于K近邻、高斯核函数或其他方法生成的。 | |
| 2.计算拉普拉斯矩阵 | 拉普拉斯矩阵是度矩阵D与相似度矩阵W的差,即L = D -W。拉普拉斯矩阵具有半正定性,其特征值和特征向量在谱聚类中扮演重要角色。 | |
| 3.特征值分解 | 对拉普拉斯矩阵进行特征值分解,提取最小的几个非零特征值对应的特征向量,这些特征向量构成了数据在低维空间的表示。 | |
| 4.降维 | 使用特征向量对数据进行降维,将数据映射到低维空间中。 | |
| 5.聚类 | 在低维空间中,使用传统的聚类算法(如K-means)对数据进行聚类。 |
优缺点
优势:在于它能够处理非球形簇和高维数据,对于复杂形状的数据集,谱聚类通常能提供更好的聚类效果。
缺点:计算拉普拉斯矩阵的特征值和特征向量的复杂度较高,且对参数敏感,这些是谱聚类需要克服的难题。
算法应用
谱聚类:用于图像分割、社交网络分析、生物信息学等领域。
例如:在社交网络中,谱聚类可以用来发现社区结构,即识别出网络中紧密连接的用户群体。
二. 损失函数
1. 四种损失函数
损失函数:表示预测与真实答案的距离。(交叉熵是一个比较好的损失函数)
以下是常见的用于回归和分类的损失函数:
1.1. 用于回归的损失函数
- 平方损失函数(均方误差,MSE)
- 公式: L ( Y , f ( x ) ) = ( Y − f ( x ) ) 2 L(Y,f(x))=(Y - f(x))^{2} L(Y,f(x))=(Y−f(x))2
- 特点:
- 衡量的是模型预测值与真实值之间差异平方的平均值。
- 对异常值比较敏感,因为较大的误差对损失函数的贡献更大。
- 在回归问题中广泛使用。
- 绝对损失函数(平均绝对误差,MAE)
- 公式: L ( Y , f ( x ) ) = ∣ Y − f ( x ) ∣ L(Y,f(x))=\vert Y - f(x)\vert L(Y,f(x))=∣Y−f(x)∣
- 特点:
- 对异常值(outliers)的敏感度较低,因为它不像平方损失函数那样对大的误差进行平方。
- 其梯度在误差为零的点上为零,这可能导致优化算法(如梯度下降)在这些点上难以收敛。
1.2. 用于分类的损失函数
- 0 - 1损失函数
- 公式: L ( Y , f ( x ) ) = { 1 , Y ≠ f ( x ) 0 , Y = f ( x ) L(Y,f(x))=\begin{cases}1, & Y \neq f(x) \\0, & Y = f(x)\end{cases} L(Y,f(x))={1,0,Y=f(x)Y=f(x)
- 特点:
- 用于衡量模型预测与真实标签之间的差异。
- 通常用于分类问题,但由于其非凸性和不连续性,在实际优化中较少直接使用。
- 交叉熵损失函数
- 二分类问题公式: C = − y ′ log y + ( 1 − y ′ ) log ( 1 − y ) C=-y'\log y+(1 - y')\log(1 - y) C=−y′logy+(1−y′)log(1−y)(其中(y)表示真实标签,(y’)表示预测标签)
- 多分类问题公式: C = − ∑ j = 1 n y j ′ log y j C =-\sum_{j=1}^{n}y'_{j}\log y_{j} C=−∑j=1nyj′logyj
- 特点
- 在神经网络中分类问题较常使用。
- 能够很好地衡量分类模型的预测概率分布与真实概率分布之间的差异,广泛应用于逻辑回归、神经网络等分类算法中。
2. 损失函数的优化(见后)
损失函数的优化算法:比如梯度下降法
三. 泛化:交叉验证:K折验证
在机器学习中,泛化(Generalization)是指模型对新的未见过的数据进行预测的能力。一个具有良好泛化能力的模型能够捕捉到数据的潜在规律,而不是仅仅记住训练数据。
泛化是机器学习中的一个核心目标,因为它关系到模型在实际应用中的有效性和可靠性。
交叉验证(Cross-Validation)是一种统计分析方法,用于评估并提高模型的预测性能。它是一种分割数据的技术,目的是想要测试模型在独立数据集上的表现。交叉验证的主要目的是通过减少 数据分割的偏差来提高模型评估的准确性。
交叉验证的基本步骤
| 步骤 | 描述 |
|---|---|
| 数据分割 | 将原始数据集分割成几个子集。通常,数据集会被分割成K个大小相等的子集。 |
| 模型训练与验证 | 对于K个子集,进行K次训练和验证,每次选择其中一个子集作为验证集,剩下的K - 1个子集作为训练集。使用训练集来训练模型,然后使用验证集来评估模型的性能。 |
| 结果平均 | 记录每次验证的结果,然后计算这些结果的平均值,以得到模型的整体性能评估。 |
交叉验证常用的是:
K折交叉验证(K - Fold Cross - Validation),将数据集平均分割成K个大小相等的子集;每次选择一个子集作为验证集,其余K - 1个子集作为训练集,重复K次,每次选择不同的子集作为验证集。

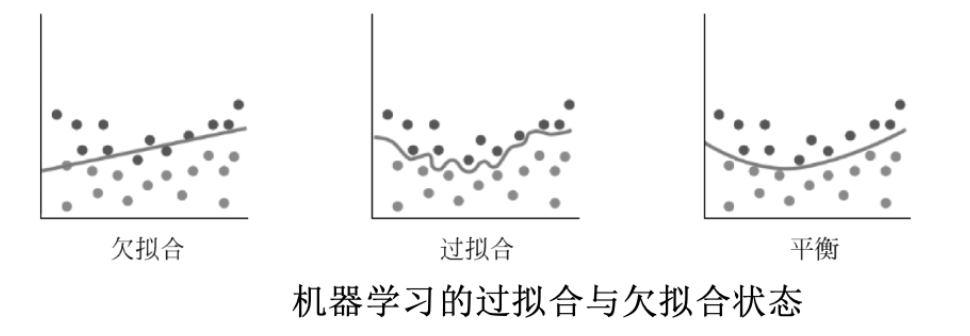
四. 过拟合与欠拟合
欠拟合(Underfitting)指的是模型在训练集和测试集上表现都很差,
过拟合(Overfitting)指的是模型在训练集上表现良好但在测试集上表现很差,即泛化性能不好。
1. 欠拟合解决办法
| 序号 | 解决办法 | 具体描述 |
|---|---|---|
| 1 | 增加特征数量 | 欠拟合可能是因为模型没有足够的特征来捕获数据中的关键信息,添加更多相关的特征可以提高模型的泛化能力。可以考虑加入特征组合、高次特征,以此增大假设空间。 |
| 2 | 增加模型复杂度 | 欠拟合通常是因为模型过于简单而无法适应数据的复杂性。增加模型的复杂度,例如增加神经网络的层数、增加决策树深度或增加多项式次数,可以提高模型性能。 |
| 3 | 减少正则化参数 | 在欠拟合情况下,可能需要减少正则化的程度或完全去除正则化。 |
| 4 | 增加训练数据 | 更多的训练数据可以提供更多的信息,有助于模型更好地泛化。 |
| 5 | 改进特征工程 | 仔细选择和构建特征可以帮助模型更好地适应数据。确保特征工程是合适的,可以提高模型的性能。 |
| 6 | 使用更复杂的算法 | 如果欠拟合问题无法通过调整模型复杂度来解决,可以考虑使用更复杂的机器学习算法,如深度学习模型或集成学习方法。 |
| 7 | 使用集成学习 | 集成学习方法,如随机森林和梯度提升树,可以将多个模型组合在一起,以提高整体性能。 |
2. 过拟合解决办法
| 序号 | 解决办法 | 具体描述 |
|---|---|---|
| 1 | 权值衰减 | 在神经网络训练过程中,通过乘一个小于1的因子(例如0.9,通常称为衰减率)来减小权重的绝对值。这种方法通过惩罚过大的权重值,有助于减少模型的复杂度和过拟合风险。 |
| 2 | 提前停止训练 | 通过早停法(Early Stopping)避免过拟合。在训练过程中监测验证集的性能,并在验证性能不提升时提前停止训练,有助于防止模型在训练数据上过拟合。 |
| 3 | 正则化 | 在目标函数(也称代价函数或损失函数)中加入正则项(如L1或L2正则化),以惩罚大的权重值。L1正则化倾向于生成稀疏权重矩阵,而L2正则化倾向于更平滑的权重调整。正则项的系数(通常称为lambda或alpha)表示正则化的强度,有助于控制模型复杂度,防止过拟合。 |
| 4 | 减少模型参数 | 过拟合通常发生在模型具有过多参数、过于复杂的情况下,因为这些参数容易记住训练数据的细节,而不是学习到通用的模式。减少模型参数的方法包括减少层数、减少每层神经元数量、选择简单的模型架构等。 |
| 5 | Dropout | Dropout是一种正则化技术,通过在训练过程中随机将一部分神经元的输出设置为零(或者说“丢弃”它们),来减少神经网络的复杂性,从而降低过拟合的风险。 |
| 6 | 数据增强 | 数据增强通过对训练数据进行一系列随机变换或扩充,生成新的训练样本,从而增加了训练数据的多样性。这有助于模型更好地泛化到新数据上,减少过拟合的风险。 |
| 7 | 决策树剪枝 | 决策树剪枝通过修剪(删除)决策树的一些分支或叶节点来降低树的复杂性,从而提高了模型的泛化能力。 |
| 8 | 交叉验证 | 使用交叉验证方法,如K折交叉验证,可以帮助检测模型是否在不同的数据子集上都表现良好,从而减轻了过拟合的风险。 |
























 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










