文章目录
本章需要掌握内容
- 理解线性方程组解的概念.
- 非齐次线性方程组
Ax = b可能有解(唯一解或无穷多解),亦可能无解,要理解方程组有解的充要条件是秩r(A) = r(Ā). - n元齐次方程组Ax = 0 有非零解的判断方法是检查
r(A) < n,或检查行列式 | A | = 0。
要理解基础解系这一概念,其实它就是解向量的极大线性无关组(一般都能化成单位矩阵?),要掌握基础解系的求法与证明. - 要熟悉线性方程组解的性质,掌握解的结构,熟练运用初等行变换求通解(特解、导出组基础解系)。
一. 基本内容与重要结论
1. 线性方程组的定义
1. 非齐次线性方程组、齐次线性方程组
2. 一组解与全部解
3. 方程组的增广矩阵与系数矩阵
4. 方程组的矩阵表示
2. 线性方程组的初等变换
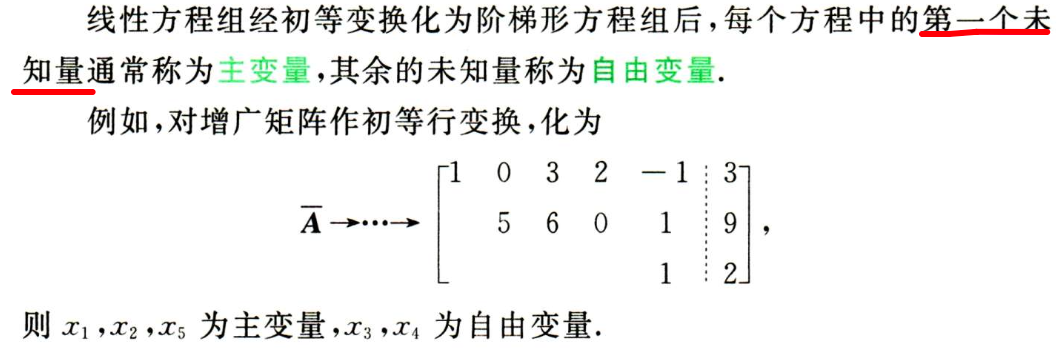
1. 初等变换
2. 主变量与自由变量的概念(主要用于得出基础解系ing)
3. 基础解系
1. 基础解系的特点
2. 齐次方程组的通解
注意:基础解系不唯一
二. 主要定理
1. 初等行变换可得同解方程组
2. 解的情况
- 情况矛盾
- 秩r(A) = r(Ā) 有唯一解:每一个参数都有限制
- r < n 说明有些参数并未限制,有些未知数可以随意写。
3. 齐次有解的定理
n阶齐次线性方程组
因为如果秩等于n,化成行阶梯矩阵,只能得到0解,与非零解矛盾。
4. (齐次)基础解系的构成ing

5. 非齐次有解定理

6. 解的性质与结构










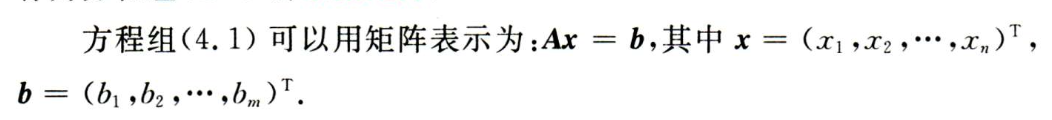
























 5196
5196

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










