这篇博客聚焦《数据结构导论》中的树和森林，讲解它们在自考和期末考试中的备考要点。内容包括树与二叉树的转换、遍历方法，以及森林的遍历策略。树转换成二叉树的关键在于兄弟结点的连接和旋转，而森林转换成二叉树则涉及根结点的兄弟关系。树的遍历包括先序、后序和层次遍历，森林的遍历则分为先序和中序两种方式。对于自考，这些转换和遍历是重点，建议加强练习。
树和森林
这篇博客继续我们的《数据结构导论》课程，今天重点说说树和森林怎么备考自考和通过期末考试。
在开始之前，上篇博客最后其实还有一点没有写完，就是如何通过已知序列，恢复一棵二叉树
看例题吧
假设一棵二叉树的中序序列与后序序列分别为：BACDEFGH 和 BCAEDGHF 建立该二叉树
这种题目的解法，其实还是考察树的遍历
先看后序序列，后序序列的最后一个结点，也就是F，一定是根结点，为啥？想想吧
有根结点了，在看中序序列中 F左侧的BACDE左子树，F右侧的GH右子树
然后一遍遍的重复这个顺序，看后序序列 BCAED / GH 中，D，H是左右子树的跟结点
看中序序列 BAC D E / G H
所以 D的左子树 包含BAC结点，H的左子树包含G结点，不包含右结点
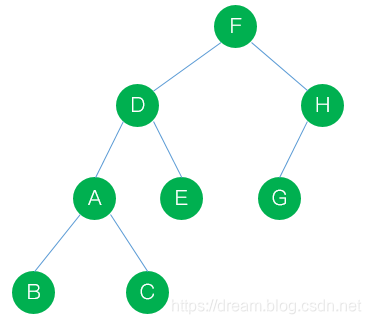
剩下的就交给你自己吧，最终要实现如下图所示即可
树的存储结构（该部分内容，近20年自考试卷中无涉及，过吧）
- 孩子链表 表示法
- 孩子兄弟链表 表示法
- 双亲 表示法
订阅专栏 解锁全文
扫一扫
1万+
到【灌水乐园】发言
