SVM支持向量机的核函数到底是干嘛的？-Note

原创于 2024-07-02 18:01:39 发布 · 368 阅读

·

4

·

CC 4.0 BY-SA版权

版权声明：本文为博主原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接和本声明。

文章标签：

#支持向量机 #算法 #机器学习

核函数原理

低纬度向高纬度映射，从而便于对其分类。

简单举例：

若用一条直线在二维难以分开，

那就将所有数据通过某一个映射函数映射到三维空间，

通过某一个面进行分割，

且不用关心是映射函数。

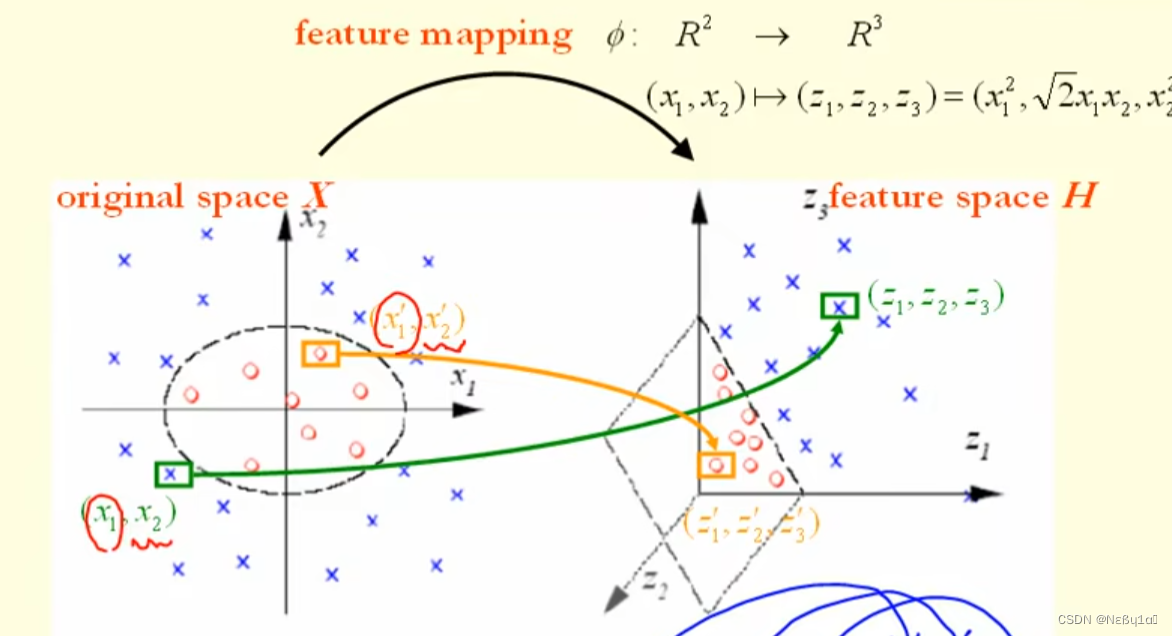
低维度向高维度映射后，通过kernel 函数进行分类， kernel函数可计算两个向量的内积：

$\phi$ 为映射函数

支持向量机的最根本的想法：用一个面进行分割两个类别

$\huge ||\phi(x)-\phi(x')||^{2} = (\phi(x)-\phi(x'))^{T}(\phi(x)-\phi(x'))$

$\huge = \phi(x)^{T}\phi(x)-2\phi(x)^{T}\phi(x')+\phi(x')^{T}\phi(x')$

$\Large=<\phi(x),\phi(x)> - 2<\phi(x),\phi(x')>+<\phi(x'),\phi(x')>$

$\huge=k(x,x)-2k(x,x')+k(x',x')$

$k(x,x)=\phi{(x)}^{T}*\phi{(x)}$

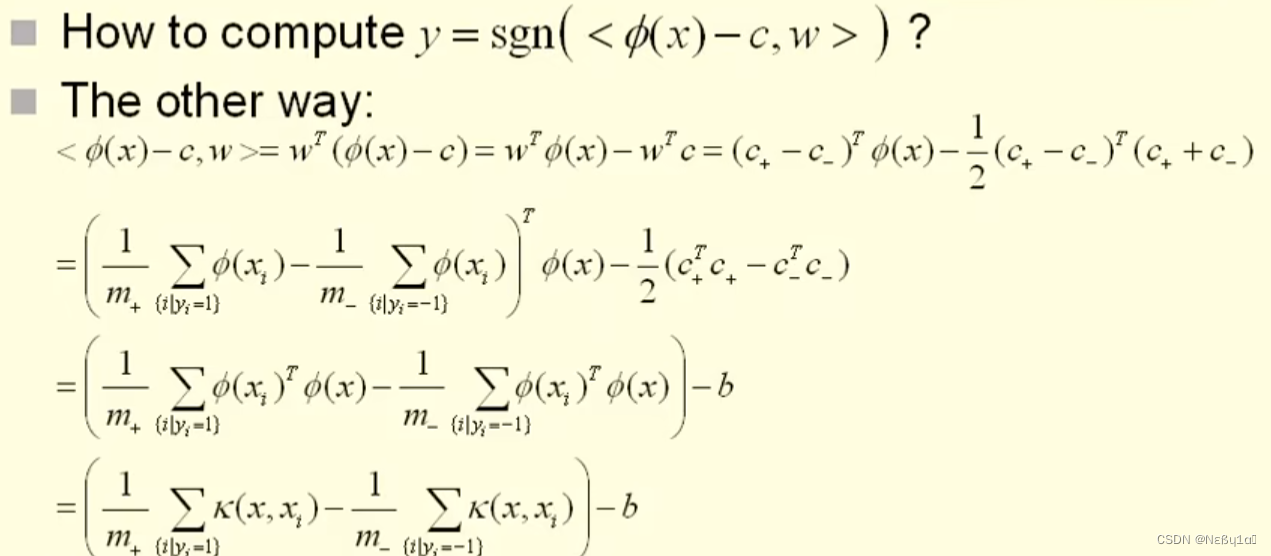
这样看结果无需关心映射关系，只需关心kernel函数k即可。

且对于kernel函数，只要函数满足半正定即

$A^{T}*A\geq 0$

线性核函数：

多项式核函数：

高斯核函数：

评论

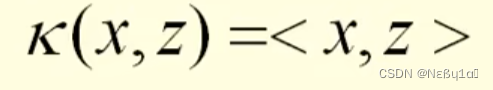
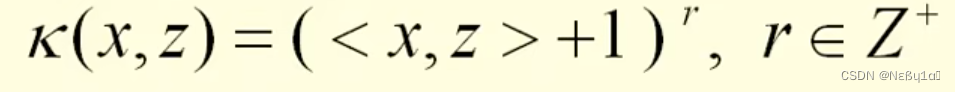
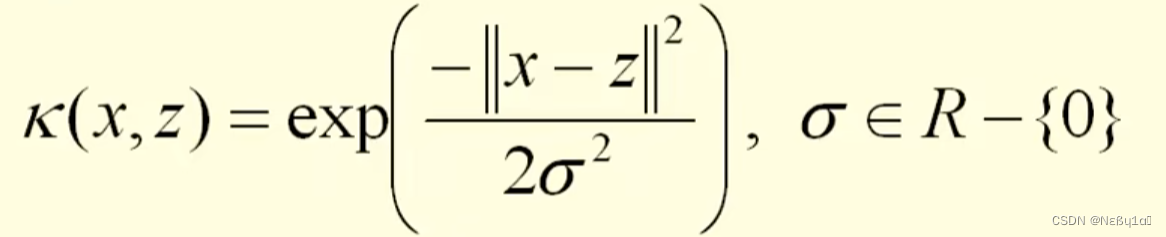
被折叠的条评论为什么被折叠?

到【灌水乐园】发言

查看更多评论

添加红包

成就一亿技术人!

hope_wisdom

发出的红包

实付元

使用余额支付

点击重新获取

扫码支付

钱包余额 0

抵扣说明：

1.余额是钱包充值的虚拟货币，按照1:1的比例进行支付金额的抵扣。
2.余额无法直接购买下载，可以购买VIP、付费专栏及课程。