A*算法的四叉树优化设计（理论）（纯文本无代码）

关于基础的a*算法请参考：Unity A星寻路算法实现

首先要理解什么是四叉树？为什么它可以达到优化的效果。它对a*算法的哪一步进行了优化？

四叉树，就是每个父节点有四个子结点的树。当在计算8邻域的寻路消耗时，若地图越大，点数越多，计算就会越多，效率越慢，原因在于计算冗余(均分的网格，无论有无必要均会逐个检查计算)，计算复杂度高O(n²)（二维数组遍历）

四叉树通过空间自适应分辨率和用空间复杂度换取时间复杂度获取更高的搜索效率，这两处加粗会在后文讲解。

先看一下在计算前需要做的准备工作。

1. 绘制四叉树

如果有看过图形学Games101的小伙伴，可以参考一下L14的Spatial Partitions空间划分

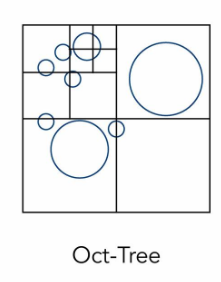
（感觉这个图错了，图是四叉树，但OctTree是八叉树的意思，四叉树是Quad Tree）

在A*中，也是类似的划分A*将点分为两大种，不可通过（障碍，已走过，越界）；可通过。

上述图是什么意思呢？四叉树构建步骤详解

1. ​​初始划分​​：将整个空间（如地图）划分为 ​​4个大小相等的矩形区域​​（象限）。

2. ​​递归评估与标记​​：对每个子区域检查其内部状态：

   • ​​混合状态​​（部分可通过/不可通过）→ 继续细分为4个子象限，​​递归处理​​。

   • ​​完全不可通过​​（如全为不可通过）→ 标记为“不可通过”节点，​​停止细分​​。

   • ​​完全可通过​​（如全为可通过）→ 标记为“可通过”节点，​​停止细分​​。

3. ​​终止条件​​：满足以下任一条件时停止细分：

   • 达到最大递归深度（防止无限细分）。

   • 达到预设的 ​​最小细分精度​​（如单像素/网格单元级别）。

   • 节点已为“完全可通过”或“完全不可通过”。

4. ​​生成树结构​​：

   • 最终形成一棵树，其中：

     • ​​叶节点​​：标记为可通过或不可通过。

     • ​​非叶节点​​：表示仍需进一步细分的混合区域。

此时树已经构建好了并且有了完整的点与点直接的关系，同时不难看出，空间自适应分辨率已经实现了。要注意不得不提且万分重要的一点，叶子结点的方向顺序是固定且不变的，这与后续计算邻域方式息息相关，此处按照：西北、东北、西南、东南的象限顺序。

2.显式转图（非必要）或动态计算邻接关系

此时虽然降低了时间复杂度，但不难发现找到8邻域似乎并不方便了，我们需要根据固定好的叶子结点方向顺序找到规律或构建邻接表。

例如，以第四个叶子结点（西南方向）为例：（上北下南）

图为：（绿色为终点，红色为起点，对钩表示可通过，错号表示不可通过）：左为地图，右为树

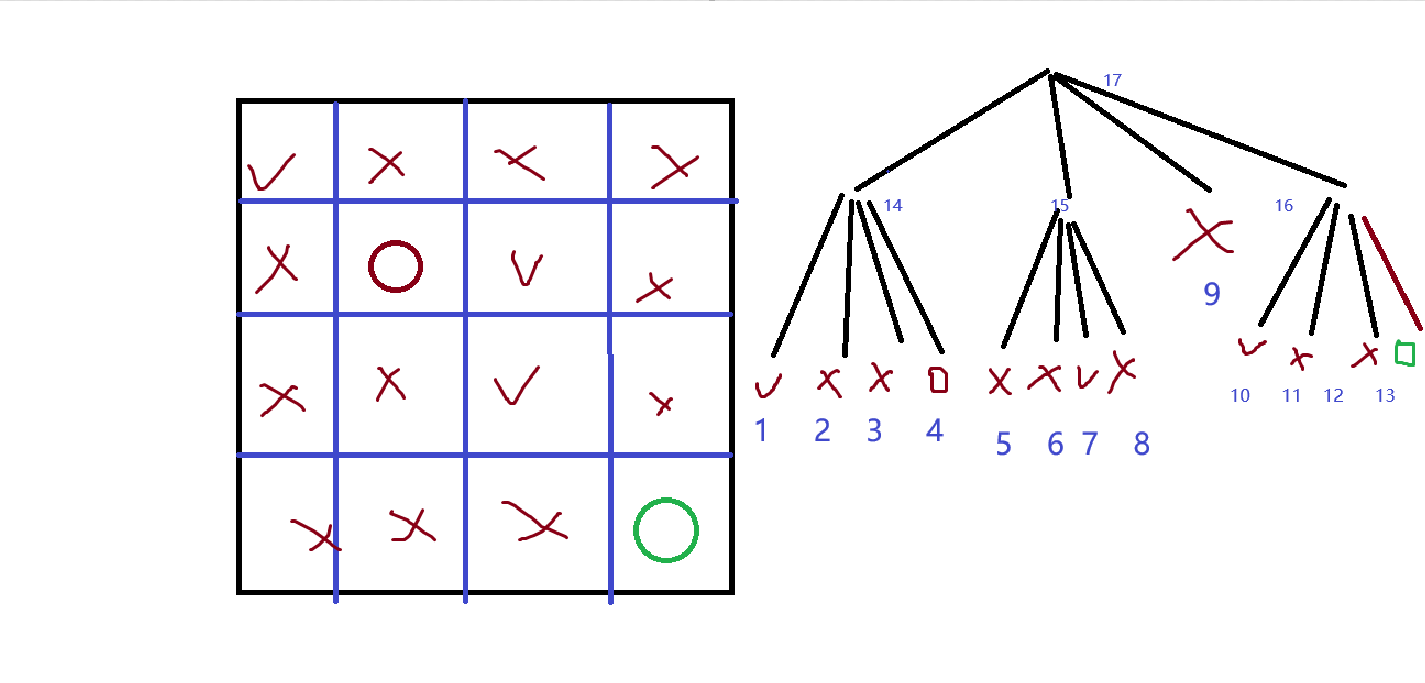
其八个方向为	结点为
西北	1（同级第一个结点）
北	2（同级第二个结点）
东北	5（父级第二个结点的第一个子结点）
西	3（同级第三个结点）
东	7（父级第二个结点的第三个子结点）
西南	9（父级第三个结点的第一个子结点（没有子节点，采用父结点的标签））
南	9（父级第三个结点的第二个子结点（没有子节点，采用父结点的标签））
东南	10（父级第四个结点的第一个子结点）

此表格仅为西南方向计算邻域表格，其他三个象限需要另外计算，作者懒了此处。如果是边界怎么处理啊作者？很简单，当成不可通过的点使用就好了。

此时发现找到了一种固定的连接方式，为了方便计算，我们可以把他们连接起来做成邻接表，虽然这会损坏四叉树的完美结构，但他可以在更复杂的地图中大幅度提高计算效率（我们无需通过父节点找到目标邻域）。

3. A*寻路

1. 确定起始点和终点所在的四叉树叶节点​​

• ​​起始点：从四叉树的根节点开始，递归检查其所在的象限，直到找到包含该点的 ​​最小叶节点​​（即不再细分的节点）。

• ​​终点：同理，递归查找终点所在的叶节点。

2.寻路

• ​​起始点加入关闭列表，修改标签，开启列表加入八邻域并计算消耗

• ​​选取消耗最小的点修改标签，加入关闭列表，并再次选取八邻域，递归

• 直至开启列表为空（死路）或到达目标点结束寻路计算

3. 美化一切

        发挥各位创造者的智慧制作出完美的敌人寻路吧！！！