Python__数据结构与算法——树、二叉树（实现先、中、后序遍历）

目录

一、树

二、二叉树

---

树和前面所讲的表、堆栈和队列等这些线性数据结构不同，树不是线性的。在处理较多数据时，使用线性结构较慢，而使用树结构则可以提高处理速度。不过，相对于线性的表、堆栈和队列等线性数据结构来说，树的构建便显得复杂了。

一、树

树是一种非线性的数据结构，如图-1 所示，之所以称之为树，是因为其形状像一棵倒置的树。每颗树都有一个根节点，如图-1 所示的树中，Root 为根节点。A、B、C 为 Root 的儿子，Root 为 A、B、C 的父亲。A、B、C 为兄弟。同样，A 为 D、E 的父亲，D、E 为 A 的儿子，D、E为兄弟。D、E为 Root 的孙子，Root 为 D、E 的祖父。在树中，如果一个元素没有儿子，则称之为树的叶子。

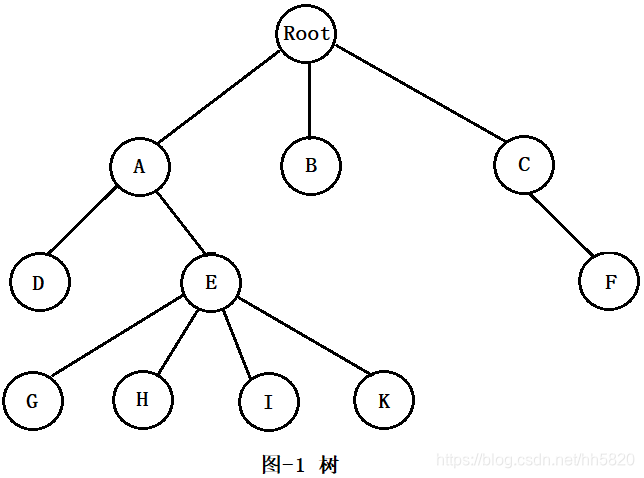
在 Python 中，树的实现可以使用列表或者类的方式。使用列表的方式较为简便，但树的构建过程较为复杂。使用类的方式构建树时，需要首先确定树中的节点所能拥有的最大儿子数。因为每个节点所拥有的儿子数量并不一定相同，因此使用类的方法将占用更大的存储空间。

如下所示的 pytree.py 脚本，以列表的形式构建了图-1所示的树。

# -*- coding:UTF-8 -*-
# file: pytree.py

G = ['G', []]  # 构造叶子 G，树中每个元素都由该元素的值和该元素的儿子列表组成
H = ['H', []]  # 构造叶子 H
I = ['I', []]  # 构造叶子 I
K = ['K', []]  # 构造叶子 K
E = ['E', [G, H, I, K]]  # 构造 E 节点
D = ['D', []]  # 构造叶子 D
F = ['F', []]  # 构造叶子 F
A = ['A', [D, E]]  # 构造 A 节点
B = ['B', []]  # 构造叶子 B
C = ['C', [F]]  # 构造 C 节点
Root = ['Root', [A, B, C]]  # 构造树根
print(Root)

输出结果：

C:\Users\图图\AppData\Local\Programs\Python\Python37-32\python.exe D:/Python/pytree.py
['Root', 
[['A', [['D', []], ['E', [['G', []], ['H', []], ['I', []], ['K', []]]]]], 
['B', []], 
['C', [['F', []]]]
]]

Process finished with exit code 0

二、二叉树

二叉树是一类比较特殊的树，在二叉树中每个节点最多只有两个儿子，分为左和右，如图-2 所示。相对于树而言，二叉树的构建和使用都要简单得多。

任何一棵树，都可以通过变换转换成一棵二叉树。

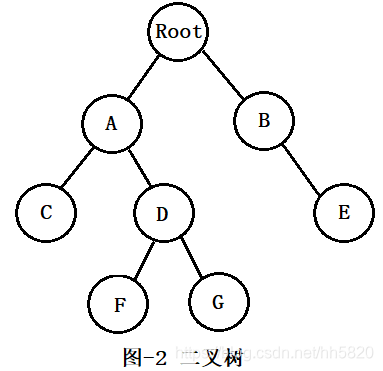
在 Python 中，二叉树的构建和树一样，可以使用列表或者类的方式。由于二叉树中的节点具有确定的儿子数，因此，使用类的方式更为简便。下面所示的 pytree.py 用较为简单的方式生成了如图-2所示的树。

# -*- coding:UTF-8 -*-
# file: pytree.py


class Btree:  # 二叉树节点
    def __init__(self, value):  # 初始化函数
        self.left = None  # 左儿子
        self.data = value  # 节点值
        self.right = None  # 右儿子

    def insertLeft(self, value):  # 向左子树插入节点
        self.left = Btree(value)
        return self.left

    def insertRight(self, value):  # 向右子树插入节点
        self.right = Btree(value)
        return self.right

    def show(self):  # 输出节点数据
        print(self.data)


if __name__ == '__main__':
    Root = Btree('Root')  # 根节点
    A = Root.insertLeft('A')  # 向根节点中插入 A 节点
    C = A.insertLeft('C')  # 向 A 节点中插入 C 节点
    D = A.insertRight('D')  # 向 A 节点中插入 D 节点
    F = D.insertLeft('F')  # 向 D 节点中插入 F 节点
    G = D.insertRight('G')  # 向 D 节点中插入 G 节点
    B = Root.insertRight('B')  # 向根节点中插入 B 节点
    E = B.insertRight('E')  # 向 B 节点中插入 E 节点
    Root.show()  # 输出节点数据
    Root.left.show()
    Root.right.show()
    A = Root.left
    A.left.show()
    Root.left.right.show()

输出结果：

当创建好一棵二叉树后，可以按照一定的顺序对树中所有的元素进行遍历。按照先左后右，树的遍历方法有三种：先序遍历、中序遍历和后序遍历。

先序遍历的次序——如果二叉树不为空，则先访问根节点，然后访问左子树，最后访问右子树；否则，程序退出。

中序遍历的次序——如果二叉树不为空，则先访问左子树，然后访问根节点，最后访问右子树；否则，程序退出。

后序遍历的次序——如果二叉树不为空，则先访问左子树，然后访问右节点，最后访问根子树；否则，程序退出。

下面所示的 TreeTraversal.py 脚本使用了三种遍历方式遍历图-2 所示的树。

# -*- coding:UTF-8 -*-
# file: TreeTraversal.py


class BTree:  # 二叉树节点
    def __init__(self, value):  # 初始化函数
        self.left = None  # 左儿子
        self.data = value  # 节点值
        self.right = None  # 右儿子

    def insertLeft(self, value):  # 向左子树插入节点
        self.left = BTree(value)
        return self.left

    def insertRight(self, value):  # 向右子树插入节点
        self.right = BTree(value)
        return self.right

    def show(self):  # 输出节点数据
        print(self.data)


def preorder(node):  # 先序遍历
    if node.data:
        node.show()
        if node.left:
            preorder(node.left)
        if node.right:
            preorder(node.right)


def inorder(node):  # 中序遍历
    if node.data:
        if node.left:
            inorder(node.left)
        node.show()
        if node.right:
            inorder(node.right)


def postorder(node):  # 后序遍历
    if node.data:
        if node.left:
            postorder(node.left)
        if node.right:
            postorder(node.right)
        node.show()


if __name__ == '__main__':
    Root = BTree('Root')  # 构建树
    A = Root.insertLeft('A')
    C = A.insertLeft('C')
    D = A.insertRight('D')
    F = D.insertLeft('F')
    G = D.insertRight('G')
    B = Root.insertRight('B')
    E = B.insertRight('E')
    print('**************************')
    print('Binary Tree Pre-Traversal')
    print('**************************')
    preorder(Root)  # 对树进行先序遍历
    print('**************************')
    print('Binary Tree In-Traversal')
    print('**************************')
    inorder(Root)  # 对树进行中序遍历
    print('**************************')
    print('Binary Tree Post-Traversal')
    print('**************************')
    postorder(Root)  # 对树进行后序遍历

运行 TreeTraversal.py 脚本输出结果：

C:\Users\图图\AppData\Local\Programs\Python\Python37-32\python.exe D:/Python/TreeTraversal.py
**************************
Binary Tree Pre-Traversal
**************************
Root
A
C
D
F
G
B
E
**************************
Binary Tree In-Traversal
**************************
C
A
F
D
G
Root
B
E
**************************
Binary Tree Post-Traversal
**************************
C
F
G
D
A
E
B
Root

Process finished with exit code 0