堆排序、单链表排序

为什么要用堆排序呢？那么复杂，别的排序不行么？可能真不行呢

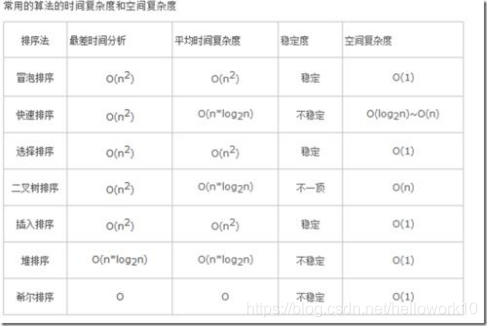
看看这个图就会发现，堆排序的时间复杂度（nlogn）空间复杂度（1），这就是为什么要选用他的原因了。其他算法你可能都会，但面试官就考堆排序，因为这个算法更优
堆是具有以下性质的完全二叉树：每个结点的值都大于或等于其左右孩子结点的值，称为大顶堆；或者每个结点的值都小于或等于其左右孩子结点的值，称为小顶堆。

算法步骤
创建一个堆 H[0……n-1]；
把堆首（最大值）和堆尾互换；
把堆的尺寸缩小 1，并调用 shift_down(0)，目的是把新的数组顶端数据调整到相应位置；
重复步骤 2，直到堆的尺寸为 1。
堆排序主要两个思想：构造堆，将元素按照一定的规则加到堆中（堆上升过程）；交换对顶和最后一个元素，将剩余的元素做堆构造；
推荐博客 https://blog.youkuaiyun.com/u010452388/article/details/81283998
我这里主要是手撕代码

package main;

public class heapSort {
   

    public static void heapSort(int[] arr){
   
        //构造堆
        heapInsert(arr);
        int size=arr.length;
        while (size>1){
   
            swap(arr,0,size-1);
            size--;
            //再次构造堆
            heapify(arr,0,size);
        }
    }
    //构造大根堆（堆中的数上升）
    public static void heapInsert(int[] arr){
   
        for (int i=0;i<arr.length;i++){
   
            int currentIndex =i;
            int fatherIndex=(currentIndex-1)/2;
            while (arr[currentIndex] > arr[fatherIndex]){
   
                swap(arr,currentIndex,fatherIndex);
                currentIndex=fatherIndex;
                fatherIndex=(currentIndex-1)/2;
            }
        }
    }
    //将剩余的数构造成大根堆（堆中的数下降）
    public static void heapify(int[] arr,int index,int size){
   
        int left=2*index+1;
        int right=2*index+2;
        while (left < size){
   
            int largestIndex;
            if (arr[left] < arr[right] && right<size){
   
                largestIndex=right;