二叉树遍历：广度优先、深度优先

最新推荐文章于 2025-05-26 00:41:44 发布

原创最新推荐文章于 2025-05-26 00:41:44 发布 · 389 阅读

0 ·

CC 4.0 BY-SA版权

文章标签：

#算法

算法专栏收录该内容

4 篇文章

订阅专栏

本文详细介绍了二叉树的遍历方法，包括广度优先（层次遍历）和深度优先（先序、中序、后序）遍历。广度优先遍历按层次从上至下，从左至右访问结点；深度优先遍历则深入每个可能的分支路径，分为先序（根左右）、中序（左根右）、后序（左右根）。同时对比了广度优先和深度优先搜索算法的特点。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

二叉树遍历：广度优先、深度优先

广度优先又叫层次遍历，从上往下对每一层依次访问，在每一层中，从左往右（也可以从右往左）访问结点，访问完一层就进入下一层，直到没有结点可以访问为止。又叫层次遍历，从上往下对每一层依次访问，在每一层中，从左往右（也可以从右往左）访问结点，访问完一层就进入下一层，直到没有结点可以访问为止。
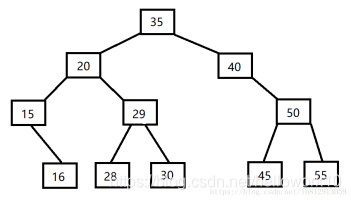
在这里插入图片描述

广度优先遍历：35 20 40 15 29 50 16 28 30 45 55

/**
     * 二叉树的广度优先遍历
     */
    public List<Integer> bfs(TreeNode root) {
        Queue<TreeNode> queue = new LinkedList<TreeNode>();
        List<Integer> list=new LinkedList<Integer>();
 
        if(root==null)
            return list;
        queue.add(root);
        while (!queue.isEmpty()){
            TreeNode t=queue.remove();
            if(t.left!=null)
                queue.add(t.left);
            if(t.right!=null)
                queue.add(t.right);
            list.add(t.val);
            }
        return list;
    }

深度优先
对每一个可能的分支路径深入到不能再深入为止，而且每个结点只能访问一次。对每一个可能的分支路径深入到不能再深入为止，而且每个结点只能访问一次。
要特别注意的是，二叉树的深度优先遍历比较特殊，可以细分为先序遍历、中序遍历、后序遍历。具体说明如下：
先序遍历：对任一子树，先访问根，然后遍历其左子树，最后遍历其右子树。
中序遍历：对任一子树，先遍历其左子树，然后访问根，最后遍历其右子树。
后序遍历：对任一子树，先遍历其左子树，然后遍历其右子树，最后访问根。

/**
     * 二叉树的深度优先遍历
     * @param root
     * @return
     */
    public List<Integer> dfs(TreeNode root){
        Stack<TreeNode> stack=new Stack<TreeNode>();
        List<Integer> list=new LinkedList<Integer>();
 
        if(root==null)
            return list;
     //压入根节点
        stack.push(root);
    //然后就循环取出和压入节点，直到栈为空，结束循环
        while (!stack.isEmpty()){
            TreeNode t=stack.pop();
            if(t.right!=null)
                stack.push(t.right);
            if(t.left!=null)
                stack.push(t.left);
            list.add(t.val);
        }
        return  list;
    }

递归的方法来实现这个深度优先遍历

public void solution(TreeNode root)
    {
        List<Integer> list=new LinkedList<Integer>();
        depthTraversal(list,root);
    }
 
    private void dfs(List<Integer> list,TreeNode tn)
    {
        if (tn!=null)
        {
            list.add(tn);
 
            //每次先添加左节点，直到没有子节点点，返回上一级
            dfs(tn.left);
            dfs(tn.right);
        }
    }

附加两种算法的进阶
深度优先搜素算法：
不全部保留结点，占用空间少；有回溯操作(即有入栈、出栈操作)，运行速度慢。
通常深度优先搜索法不全部保留结点，扩展完的结点从数据库中弹出删去，这样，一般在数据库中存储的结点数就是深度值，因此它占用空间较少。所以，当搜索树的结点较多，用其它方法易产生内存溢出时，深度优先搜索不失为一种有效的求解方法。
广度优先搜索算法：
保留全部结点，占用空间大；无回溯操作(即无入栈、出栈操作)，运行速度快。
广度优先搜索算法，一般需存储产生的所有结点，占用的存储空间要比深度优先搜索大得多，因此，程序设计中，必须考虑溢出和节省内存空间的问题。但广度优先搜索法一般无回溯操作，即入栈和出栈的操作，所以运行速度比深度优先搜索要快些。
转载：https://blog.youkuaiyun.com/lb812913059/article/details/83313360
转载：https://blog.youkuaiyun.com/XTAOTWO/article/details/83625586