在进行线性回归时，为什么最小二乘法是最优方法？

最根本的原因是哲学/逻辑。

偏差平方和，恒大于等于0。同时可以知道，这玩意是不可能达到最大值的（只要足够偏离的话，那肯定是越来越大的），因此在偏导数为0时取到的是最小值咯~（取极值的条件嘛，偏导数为0）

我们进行回归分析，自变量为x，因变量y，寻找y和x之间的连接，更确切地说x是如何求y的，所以x和y是两个本质不同的量，一个是原因，另一个是果。现在让我们来看一个主题：“我们应该使用这样一条直线，它使每一点与最小线之间的距离”。这种方法实际上是混合因果关系，试图在（x，y）向量空间中找到最佳的超平面。没有错误，这至少是一种非自然的逻辑。最小二乘法的逻辑更为自然。例如，我有一个因变量y和两个独立变量，X1，x2，它们用我观察到的样本中的一个向量表示。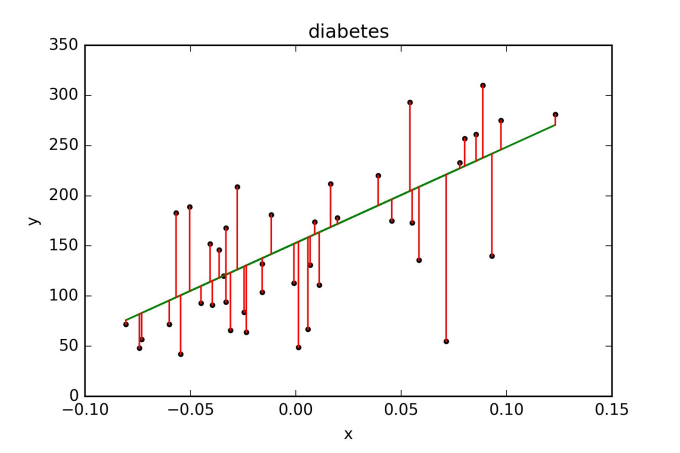

最小二乘法是做什么的？它是由观察向量X1和x2生成的线性空间中观察到的y向量的最近点。从几何的观点来看，这是正交投影。许多答案不一定是最小二乘法的最好，我们也可以使用其他距离。这很好，但最小二乘法的优势正是它的“自然”。我们最习惯的空间是带内积的欧氏空间。如果我们使用其他距离，就没有“自然”的内积。如果没有这个距离，最小方差（蓝色）的属性就消失了。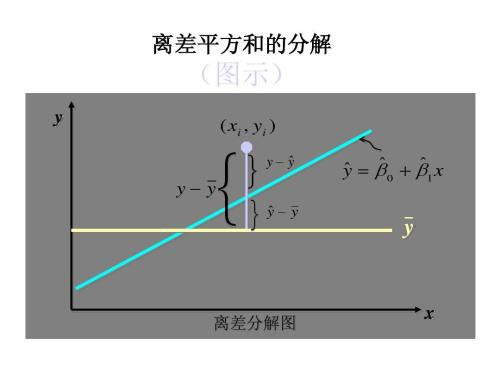

如果没有这样的距离，就假定噪声服从另一个分布。我回答了这个问题（为什么很多变量可以用正态分布来描述）？人们解释了为什么喜欢使用正态分布假设。

在更高的点上，现代科学的全部方法是“归纳”和“演绎”两种。从归纳的角度看，在实际问题中应该使用什么样的噪声？应该采用什么样的分配方式？从演绎的角度来看，哪种方法最自然，最美，最容易理解的就是尝试使用这种方法。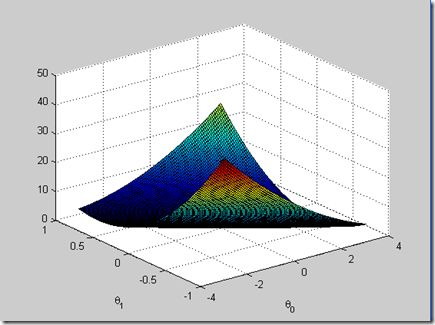

欧氏距离是最自然、最直观的距离，正态分布是最常见、最容易处理的噪声分布，自然最小二乘法是最好的方法。