本文深入探讨了导数的概念，强调了它在几何上的意义——求函数图像上某点的切线斜率。介绍了如何计算导数，包括重要三角函数的导数和反函数的导数。此外，还讲解了微分的计算及其在近似计算中的应用，并讨论了隐函数求导的方法。文章最后提到了函数n次求导后的形式以及一些常用的等价关系。
导数
导函数是一个重要的函数，它赋予了函数全新的意义
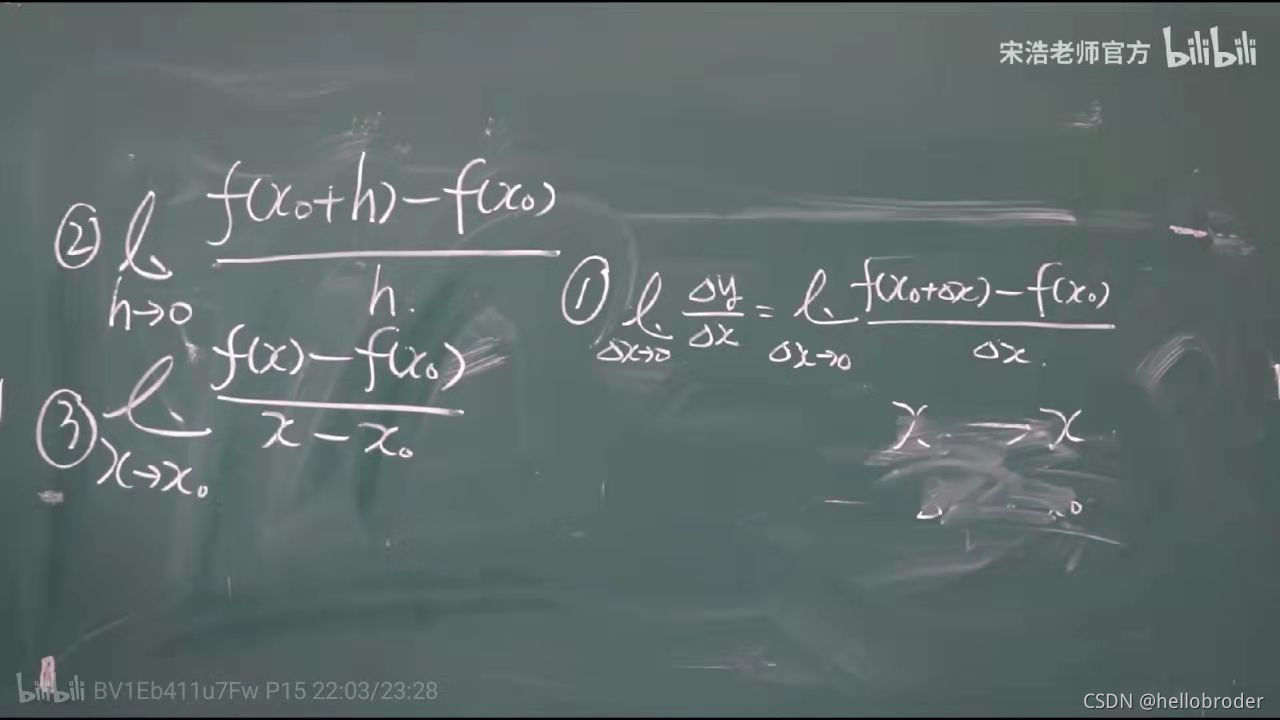
根据定义去计算一个函数的导函数
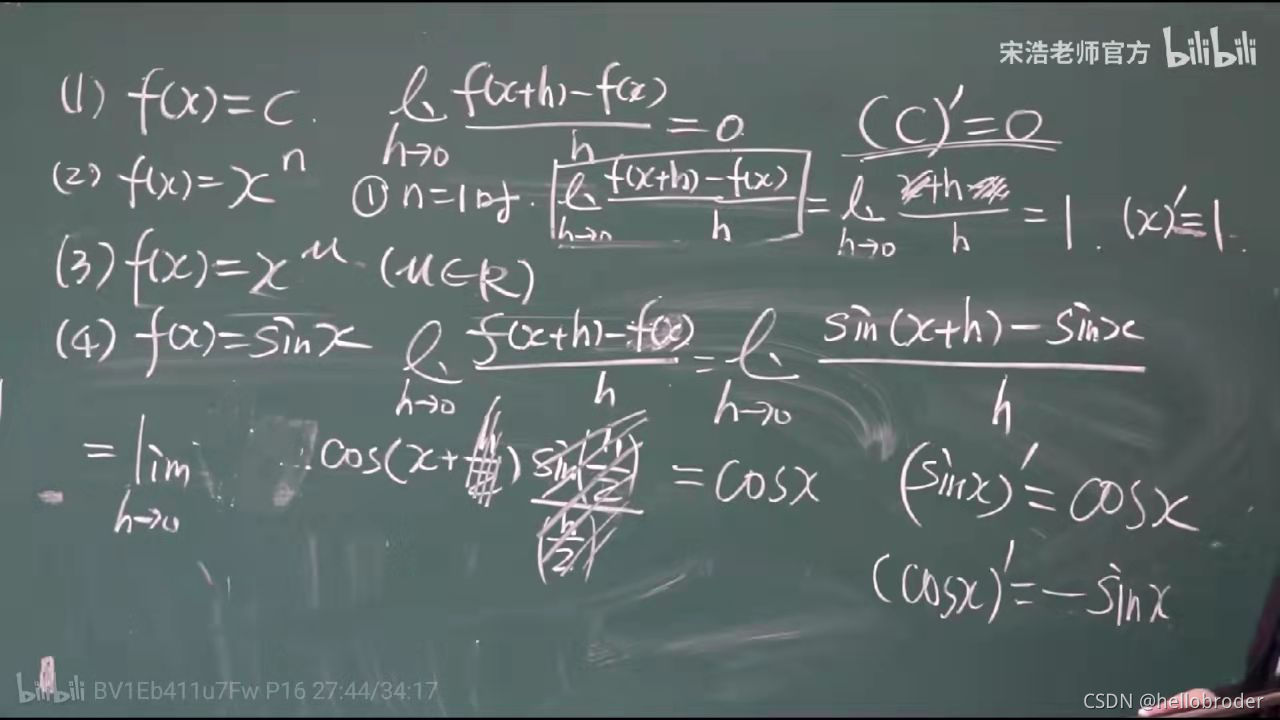
只有函数在每个点左右导数存在且相等时该函数可导
导函数的几何意义：对一个点求导相当于求在函数图像上这个点的切线斜率
几个重要三角函数的导数
如何对反函数求导
实际上一个函数的反函数的导数相当于导数切线斜率的余角的正切值
对于一些函数的求导的简易过程
微分即为微商
其中表达式中的A即为该点的导数
一些导数n次求导后的函数
一些常用的等价关系
函数和的n次求导后的形式
隐函数求导：即不能直接求导，而是隐藏在表达式中，并且求导后右侧含有原来函数
主要通过左右两侧同时求导后通过移项拼凑形成
微分的几何意义类似于导数的几何意义
一个重要函数的求导过程
通过插空寻找可求导区间
可微即可导
并且A与x的差值无任何关系 
微分的公式以及运算法则
当x的差值趋于0时，dy与三角形y近似相等
微分在近似计算中的应用的简单演绎
扫一扫
4万+
被折叠的 条评论
为什么被折叠?
到【灌水乐园】发言
