AVL树操作分析与实现

最新推荐文章于 2024-03-19 00:41:19 发布
最新推荐文章于 2024-03-19 00:41:19 发布
阅读量420 收藏 1
点赞数
CC 4.0 BY-SA版权
文章标签： AVL树 数据结构
版权声明：本文为博主原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接和本声明。
本文链接：https://blog.youkuaiyun.com/hello_world_ww/article/details/45620957

 AVL树是绝对的平衡二叉树。(貌似很吸引人的样子……)

    不过增删的操作复杂度过高，应用不如红黑树广，故而很少有详细分析AVL树操作的文章。我花了两天时间还有好几页纸终于是把这货整出来了。

    基本的二叉树操作，如查找前驱后继，左旋右旋不再赘述，只讨论AVL的插入删除。(我已经假设你看过AVL树，只是有些操作不太清楚……)当然，平衡因子左加右减。

    实现AVL树时，最好也像红黑树一样设置哨兵叶子，以便调整恢复AVL性质时的归一化而不需要在去做复杂的判定。(当然在某些查找或修改时注意判断，不要操作失效……) 

      注：设子树X的平衡因子为F(X)，高度为H(X)，左子树为L(X)，右子树为R(X)

    AVL树——插入：

    1).像世界上所有排序二叉树一样，把新的结点的平衡因子设置为0，然后插入当前保持AVL性质的二叉树T中。(千万注意不要插到哨兵后面去……)    

    2).从插入的结点开始，递归向上回溯(记得判断是否到树根)，过程如下：

        a).判断当前结点是父结点的左孩子还是右孩子：如果是左孩子则给父结点平衡因子+1，否则对平衡因子-1，代表当前插入结点对所在子树平衡性的影响

        b).如果父亲结点的平衡因子为0，说明插入节点后以父节点为根的子树高度没有发生变化且该子树没有失衡，直接结束处理；如果父亲结点的平衡因子在[-1，1]中，说明当前子树仍然保持平衡，但子树高度发生变化，递归向上处理父结点；否则此时以此父结点为根的子树失去平衡，需要平衡处理

        此过程直到遇到根直接返回原树T或者遇到失衡子树返回调整后的树T‘！之所以调平最小失衡子树后平衡调整过程就可以结束，是因为在调整失衡子树后整棵子树的高度恢复到了插入结点之前的高度，不再影响其他部分。   

        插入平衡处理：     (注：后面分析均以失衡结点因子=2为例，即失衡子树左偏)

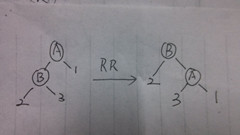
        对于左偏失衡的情况，基本的方法是右旋失衡子树。不过由于树旋转的特性，右旋树时树根左子的右孩子会挂到根结点左孩子的位置，如下图子树2：

    

        如果F(B)>=0，那么直接旋转树A做平衡调整！

        若此时F(B)<0(右偏)，即H(2)>H(C)，那么直接旋转树A将导致树A右偏失衡，所以此时需要对右偏的子树B进行左旋调整。

        不过此时的调整并非是为了调平的旋转，而是为了防止这种平衡性逆转的情况出现而做的处理，我称其为“偏置旋转”(相对于"平衡旋转")。

        树旋转本身没什么技术含量，不过因为AVL树旋转时需要考虑平衡因子的修正，故而略麻烦一点。所以在每次树旋转之前，需要先行一步平衡因子的矫正(这才是在关键所在啊……)

        当然此处我先说一下偏置右旋的平衡因子调整，如下图：

        

        F(A)==1，即进行偏置右旋。分情况讨论：

        1).F(B)==1:    显然有H(2)-H(3)==1，R(A)没有变化，L(A)的高度从H(2)+1( 因为H(2)>H(3) )变为H(3)，子树A旋转后L(A)高度减小了2，所以F(A)修正F(A)-=2；L(B)没有变化，R(B)的高度从H(3)变为H(1)+1( 因为H(2)==H(1)>H(3) )，子树A旋转后R(B)的高度增加了2，所以F(B)修正F(B)-=2

        2).F(B)==0:    显然有H(2)==H(3)，L(A)的高度从H(2)+1变为H(2)( 因为H(2)==H(3))，F(A)修正F(A)--；R(B)的高度从H(3)变为H(3)+1，F(B)修正F(B)--

        3).F(B)==-1:   显然有H(3)-H(2)==1( 此时有H(3)==H(1)>H(2))，L(A)的高度从H(3)+1变为H(3)，F(A)修正F(A)--；R(B)的高度从H(3)变为H(3)+1，F(B)修正F(B)--        

        按此调整平衡因子后，可保证接下来的右旋操作后子树平衡因子的正确性……(左旋偏置同理……)

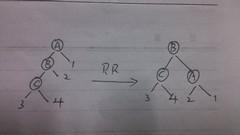
        接着再说平衡右旋～～～如下图：

        

        继续分情况讨论，此时F(A)==2，F(B)有以下三种情况(可能对B做过偏置左旋)：

        1).F(B)==0:    显然H(2)==H(C)，L(A)的高度从H(2)+1变为H(2)，F(A)修正F(A)--；R(B)的高度从H(2)变为H(2)+1(因为H(2)==H(C)==H(B)-1==H(1)+1)，F(B)修正F(B)-- 

        2).F(B)==1:    显然H(C)-H(2)==1，L(A)的高度从H(C)+1变为H(2)，F(A)修正F(A)-=2( 因为H(2)+1==H(C)==H(B)-1==H(1)+1)；R(B)的高度从H(2)变为H(2)+1，F(B)修正F(B)-- 

        3).F(B==2):    偏置旋转可能导致这种情况，不用管之～显然H(C)-H(2)==2，L(A)从H(C)+1变为H(2)，F(A)修正F(A)-=3；R(B)从H(2)变为max{ H(2)，H(1) }+1，因为H(C)-H(2)==2，H(C)-H(1)==1，所以H(1)-1==H(2)，R(B)变为H(1)+1，F(B)修正F(B)-=2

        先于平衡旋转进行因子调整后，平衡旋转即可恢复AVL树的性质！平衡左旋同理！

    AVL树——删除：

        1).按一般的二叉树删点，删除目标结点。二叉树删除特性——最终删除的点至少有一个孩子为空。

        2).以移到被删除结点位置的结点P为起点(因为有哨兵叶子，所以P不会为NULL)，递归向上回溯

                a).  判断P是其父结点的左孩子还是右孩子：如果是左孩子则给父结点平衡因子-1，否则对平衡因子+1，代表删除结点对所在子树平衡性的影响 

                b). 如果父结点的平衡因子为-1或者1，说明子树的删点没有影响到以父结点为根的子树的高度，可以直接返回。 如果父结点平衡因子为0，说明不需要调整以父结点为根的子树，继续向上回溯。如果父结点平衡因子为-2或者2，则根据不同情况按上面的方法调整，然后继续向上回溯

C++实现代码：(后面的display能打印出子字符界面的二叉树树型)

#include<iostream>
#include<string>
#include<queue>
#include<cstdlib>
using namespace std;
 
class  Node
{
public:
    Node(int x,Node* f)
    {
        value=x;father=f;
        handle=1;balance=0;
        lchild=rchild=NULL;
    }
    int id,value,handle,balance;
    Node *father,*lchild,*rchild;
};
 
Node* NewNode(int x,Node* f)
{
    Node* T=new Node(x,f);
    T->lchild=new Node(0,T);
    T->rchild=new Node(0,T);
}
 
bool IsLeaf(Node* p)
{
    if(p->lchild==NULL&&p->rchild==NULL) 
        return true;
    else return false;
}
 
Node* LRotate(Node* T,Node* p)
{
    Node* f=p->father;
    Node* r=p->rchild;
    if(r==NULL) return T;
    p->rchild=r->lchild;
    if(r->lchild!=NULL)  r->lchild->father=p;
    r->lchild=p; p->father=r;
    if(f==NULL) 
    {
        r->father=NULL;
        return r;
    }
    else 
    {
        if(f->lchild==p) f->lchild=r;
        else f->rchild=r;
        r->father=f;
        return T;
    }
}
 
Node* RRotate(Node* T,Node* p)
{
    Node* f=p->father;
    Node* l=p->lchild;
    if(l==NULL) return T;
    p->lchild=l->rchild;
    if(l->rchild!=NULL)  l->rchild->father=p;
    l->rchild=p; p->father=l;
    if(f==NULL) 
    {
        l->father=NULL;
        return l;
    }
    else
    {
        if(f->lchild==p) f->lchild=l;
        else f->rchild=l;
        l->father=f;
        return T;
    }
}
 
void LRAdjust(Node* p)
{
    if(p->balance== -2)
    {   //平衡左旋
        if(p->rchild->balance==0)
        {
            p->balance++;
            p->rchild->balance++;
        }
        else if(p->rchild->balance==-1)
        {
            p->balance+=2;
            p->rchild->balance++;
        }
        else
        {
            p->balance+=3;
            p->rchild->balance+=2;
        }
    }
    else
    {   //偏置左旋
        if(p->rchild->balance<0)
        {
            p->balance+=2;
            p->rchild->balance+=2;
        }
        else
        {
            p->balance++;
            p->rchild->balance++;
        }
    }
}
 
void RRAdjust(Node* p)
{
    if(p->balance== 2)
    {   //平衡右旋
        if(p->lchild->balance==0)
        {
            p->balance--;
            p->lchild->balance--;
        }
        else if(p->lchild->balance==1)
        {
            p->balance-=2;
            p->lchild->balance--;
        }
        else 
        {
            p->balance-=3;
            p->lchild->balance-=2;
        }
    }
    else
    {   //偏置右旋
        if(p->lchild->balance>0)
        {
            p->balance-=2;
            p->lchild->balance-=2;
        }
        else
        {
            p->balance--;
            p->lchild->balance--;
        }
    }
}
 
Node* IAdjust(Node* T,Node* p)
{
    if(p==NULL) return T;
    if(p->balance>=2) //左偏
    {
        if(p->lchild->balance<0) //右偏
        {
            LRAdjust(p->lchild); 
            T=LRotate(T,p->lchild);
        }
        RRAdjust(p);
        return RRotate(T,p);
    }
    else if(p->balance<=-2) //右偏
    {
        if(p->rchild->balance>0)   //左偏
        {
            RRAdjust(p->rchild);
            T=RRotate(T,p->rchild);
        }
        LRAdjust(p);
        return LRotate(T,p);
    }
    else   
    {
        if(p->father==NULL) return T; 
        if(p==p->father->lchild) 
            p->father->balance++;
        else p->father->balance--;
        if(p->father->balance!=0) 
            return IAdjust(T,p->father);
        else return T;
    }
}
 
Node* Insert(Node* T,int x)
{
    Node *f=NULL,*p=NULL;
    if(T==NULL) T=NewNode(x,NULL);
    else
    {
        f=p=T;
        while(!IsLeaf(p))
        {
            f=p;
            if(x<p->value)    p=p->lchild;
            else if(x>p->value) p=p->rchild;
            else {p->handle++;return T;}
        }
        delete p;p=NewNode(x,f);
        if(x<f->value) f->lchild=p;
        else f->rchild=p;
    }
    T=IAdjust(T,p);
    return T;
}
 
Node* Build(int* array,int size)
{
    if(size==0) return NULL;
    Node* T=NULL;
    for(int i=0;i<size;i++) T=Insert(T,array[i]);
    return T;
}
 
Node* Find(Node* T,int x)
{
    if(IsLeaf(T)) return NULL;
    if(x==T->value) return T;
    else if(x>T->value)
        return Find(T->rchild,x);
    else return Find(T->lchild,x);
}
 
Node* pre(Node* x)
{
    Node* p=x;
    if(!IsLeaf(p->lchild))
    {
        p=p->lchild;
        while(!IsLeaf(p->rchild)) p=p->rchild;
        return p;
    }
    else
    {
        while(p->father!=NULL&&p->father->rchild!=p) p=p->father;
        return p->father;
    }
}
 
Node* next(Node* x)
{
    Node* p=x;
    if(!IsLeaf(p->rchild))
    {
        p=p->rchild;
        while(!IsLeaf(p->lchild)) p=p->lchild;
        return p;
    }
    else
    {
        while(p->father!=NULL&&p->father->lchild!=p) p=p->father;
        return p->father;
    }
}
 
Node* DAdjust(Node* T,Node* p)
{
    if(p==NULL) return T;
    if(p->balance>=2)   //左偏
    {
        if(p->lchild->balance<0) //右偏
        {
            LRAdjust(p->lchild);
            T=LRotate(T,p->lchild);
        }
        RRAdjust(p);
        T=RRotate(T,p);
        p=p->father;
    }
    else if(p->balance<=-2) //右偏
    {
        if(p->rchild->balance>0)    //左偏
        {
            RRAdjust(p->rchild);
            T=RRotate(T,p->rchild);
        }
        LRAdjust(p);
        T=LRotate(T,p);
        p=p->father;
    }
    if(p->father==NULL) return T;
    if(p==p->father->lchild) p->father->balance--;
    else p->father->balance++;
    if(p->father->balance==1||p->father->balance==-1)   return T;
    else return DAdjust(T,p->father);
}
 
Node* Delete(Node* T,int x)
{
    Node *p=Find(T,x),*n=NULL;
    if(p==NULL) return NULL;
    if(--p->handle) return T;
    if(IsLeaf(p->lchild)&&IsLeaf(p->rchild))
    {               //双子空
        if(p->father==NULL) return NULL;
        if(p->father->lchild==p) 
            n=p->father->lchild=p->lchild;
        else n=p->father->rchild=p->lchild;
        p->lchild->father=p->father;
        delete p->rchild;
    }
    else if(IsLeaf(p->lchild))
    {               //左空
        if(p->father==NULL) 
        {
            n=T=p->rchild;
            n->father=NULL;
        }
        else
        {
            if(p==p->father->lchild)
                n=p->father->lchild=p->rchild;
            else n=p->father->rchild=p->rchild;
            n->father=p->father;
        }
        delete p->lchild;
    }
    else if(IsLeaf(p->rchild))
    {               //右空
        if(p->father==NULL)
        {
            n=T=p->lchild;
            n->father=NULL;
        }
        else
        {
            if(p->father->lchild==p)
                p->father->lchild=p->lchild;
            else p->father->rchild=p->lchild;
            n->father=p->father;
        }
        delete p->rchild;
    }
    else
    {   
        n=next(p);
        if(n==n->father->lchild)
            n->father->lchild=n->rchild;
        else n->father->rchild=n->rchild;
        n->rchild->father=n->father;
        p->value=n->value;
        p->handle=n->handle;
        delete n->lchild;
        n=n->rchild;
    }
    return DAdjust(T,n);
}
 
int depth(Node* T)
{
    if(IsLeaf(T)) return 0 ;
    int a=depth(T->lchild)+1;
    int b=depth(T->rchild)+1;
    return a>b?a:b;
}
 
string space(int n)
{
    string s=string("");
    for(int i=0;i<n;i++) s+=" ";
    return s;
}
 
void Display(Node* T,int mode)
{
    if(IsLeaf(T)) return ;
    queue<Node> Q;
    int pl=0,pid=0,H=depth(T),h=0; //pl，之前打印所在层数
    T->id=1;
    Q.push(*T);                 //pid，之前打印结点的编号
    while(!Q.empty())
    {
        Node& p=Q.front();
        for(h=0;;h++)   //当前结点在树中所在的层数
            if((1<<h)>=p.id+1) break;
        int offset=(1<<(H-h+1))-1;//本层两个结点之间的偏移量
        if(h==pl) 
        {                           //加上了结点本身的占位,当结点打印值超过1个字符位时会导致混乱                    
            cout<<space((p.id-pid)*offset)<<space(p.id-pid-1);
            if(mode) cout<<p.value;
            else cout<<p.balance;
            pid=p.id;
        }
        else 
        {
            pid=1<<(h-1); //前一次结点编号
            int of=(1<<(H-h))-1; //本层总偏移量
            cout<<endl<<space(of)<<space((p.id-pid)*offset)<<space(p.id-pid);
            if(mode) cout<<p.value;
            else cout<<p.balance;
            pid=p.id;pl=h;
        }
        Q.pop();
        if(!IsLeaf(p.lchild))
        {
            p.lchild->id=p.id*2;
            Q.push(*p.lchild);
        }
        if(!IsLeaf(p.rchild))
        {
            p.rchild->id=p.id*2+1;
            Q.push(*p.rchild);
        }
    }
    cout<<endl<<endl;
}
 
int main(int argc,char* argv[])
{
//  int array[9]={5,3,4,7,6,1,2,9,8};
    int array[9]={1,2,3,4,5,6,7,8,9};
//  int array[6]={3,2,8,5,9,6};
    Node* T=Build(array,atoi(argv[1]));
    Display(T,1);
    Display(T,0);
    if(argc==3)
    {
        T=Delete(T,atoi(argv[2]));
        Display(T,1);
        Display(T,0);
    }
    return 0;
}


hello_world_ww
关注
AVL 树应用
实践求真知
08-06 390
平衡二叉树
AVL树分析
MoMo的奋斗
04-26 627
这篇文章只专注四件事：avl树的分析；为什么会这么做？为什么我没有想到？问题出在哪里？ 相信会是一次不同以往的体验并给你带来巨大的收获。
数据结构与算法课程设计---AVL TREE的实现及分析
09-07
（1）编写 AVL树判别程序，并判别一个二元查找树是否为 AVL树。二元查找树用其先序遍历结果表示，如：5，2，1，3，7，8。 （2）实现 AVL树的 ADT，包括其上的基本操作：结点的加入和删除；另外包括将一般二元查找树转变为 AVL树的操作。
小肥柴慢慢手写数据结构（C篇）（2-1 单链表 SingleLinkedList self版实现（1））
卷毛迷你猪的博客
10-30 792
小肥柴慢慢手写数据结构（C篇）（2-1 单链表 SingleLinkedList self版实现）目录2-1 为啥要有链表2-2 出列ADT2-3 边想边写2-4 反思一下 目录 2-1 为啥要有链表 在1篇中“动态”数组ArrayList的学习中，我们发现这个动态是依靠resize操作实现的，非真正意义上的动态，因为我们需要随时关注size和capacity之间的关系。 虽然ArrayList的查询效率非常高，但是插入和删除开销大。 针对以上弱点，给出一个新的数据结构–链表。 2-2 出列ADT 节
数据结构与算法分析之--->AvlTree的实现
Elapsed_Hiyori的专栏
03-06 652
主体风格参照Weiss于《数据结构与算法分析（C语言描述）》中的AvlTree的相关描述 自己补全了AvlTree的删除等操作以及课后习题的高效率双旋转 /* Project: AvlTree */ /* Author: ZZ_InoRi/Elasped_Hiyoti */ /* Home: http://blog.youkuaiyun.com/Elapsed_Hiyori
自平衡的艺术：深入了解 AVL 树的核心原理与实现
最新发布
09-23
《 C++ 修炼全景指南：十 》自平衡的艺术：深入了解 AVL 树的核心原理与实现 https://lenyiin.blog.youkuaiyun.com/article/details/142290626?spm=1001.2014.3001.5502 我的这篇技术博客所涉及的所有完整代码。...
java数据结构与算法之平衡二叉树(AVL树)的设计与实现分析.pdf
12-08
本篇文档旨在详细探讨AVL树的设计原理、结构特点以及实现过程，为深入理解这一自平衡二叉查找树的内部机制提供一份清晰的分析。 首先，AVL树作为一种特殊的二叉查找树，其根本特性在于任何节点的两个子树的高度差不...
掌握AVL树删除操作与程序实现
#### AVL树删除操作的源代码分析 源代码中将包含上述操作的程序实现。通常，我们会定义一个AVL树节点的结构体（class或struct），并且会有如下几个核心函数： - `remove()`：主函数，用于处理节点删除逻辑。 - `...
java数据结构与算法之平衡二叉树(AVL树)的设计与实现分析.docx
12-21
### Java数据结构与算法之平衡二叉树(AVL树)的设计与实现分析 #### 普通二叉查找树的问题及解决方案 在介绍平衡二叉树之前，我们首先需要了解普通二叉查找树的一些问题。普通二叉查找树在理想情况下能够提供较快的...
AVL树的细节实现_课程设计文档+代码
12-27
6. **课程设计与毕业论文**：在课程设计或毕业论文中，可能会涉及AVL树的理论分析、算法设计、代码实现以及性能测试。文档可能包括了AVL树的定义、性质、插入和删除的详细步骤、旋转操作的逻辑和伪代码，以及实际...
AVL树实现及其性能分析
weixin_42562387的博客
05-17 1786
AVL树的提出: 二叉搜索树虽然可以缩短查找的效率, 但如果数据有序, 或者接近有序, 二叉搜索树将退化为单支树, 查找元素相当于在顺序表中搜索元素, 效率低下. 二叉搜索树实现及其性能分析 由此,1962年G.M.Adelson-Velskii和E.M.Landis两位俄罗斯数学家提出平衡二叉搜索树的方法: 当向二叉搜索树中插入新结点后, 保证每个结点的左右子树高度之差的绝对值不超过1(超过了则对树的结点进行相应的调整), 即可降低树的高度, 从而减少平均搜索长度. 概念: 一颗AVL树或者是空树, 或者
AVLTree简单实现
Runner的专栏
07-09 471
AVL树的性质 1. 左子树和右子树的高度之差的绝对值不超过1 2. 树中的每个左子树和右子树都是AVL树 3. 每个节点都有一个平衡因子(balance factor--bf),任一节点的平衡因子是-1,0,1。(每个节点的平衡因子等于右子树的高度减去左子 树的高度 ) AVL树的效率 一棵AVL树有N个节点，其高度可以保持在log2N，插入/删除/查找的时间复杂度也是log2N
[数据结构] 搜索树与AVL树
一氧化二氢的执着
03-02 543
搜索树与AVL树知识点总结
数据结构：二叉搜索树递归与非递归的实现 及性能，AVL，红黑树分析
W_J_F_的博客
06-09 439
二叉搜索树 二叉查找树(Binary Search Tree)，(二叉搜索树 或 二叉排序树)它或者是一棵空树， 或者是具有下列性质的二叉树: 若它的左子树不空，则左子树上所有结点的值均小于它的根结点的值; 若它的右子树不空，则右子树上所有结点的值均大于它的根结点的值;  它的左、右子树也分别为二叉排序树。 二叉树实现： 二叉树及二叉树的基本操作（递归与非递归） - W_J_F_的博客 ...
【数据结构高阶】终于有人把AVL树给说清了
qq_54883034的博客
07-09 880
二叉搜索树又被称为二叉排序树，它是一棵空树，或者是具有一下性质的二叉树若它的左子树不为空，则左子树上所有的节点的值都小于根节点的值。若它的右子树不为空，则右子树上所有的节点的值都大于根节点的值。它的左右子树也分别为二叉搜索树。图例： 从上述概念以及图中可以看出，二叉搜索树具有以下的特性：既然将其称为二叉搜索树，因此这颗树主要是用来进行查找元素，而且查询的原理特别简单。具体如下：题目在一棵二叉搜索树中，查找某个值，如果在树中存在这个元素，那么就返回true,否则返回false图例： 插入和删除操作，都是建立在
数据结构——AVL树
m0_72165281的博客
03-19 838
数据结构——AVL树
2024.1.5 关于 二叉平衡树（AVL 树）详解
weixin_63888301的博客
01-07 1038
二叉搜索树 二叉搜索树的简介 二叉搜索树的查找 二叉搜索树的效率 AVL树 AVL 树的简介 AVL 树的实现 AVL树的旋转 右单旋 左单旋 左右双旋 右左双旋 完整 AVL树插入代码 验证 AVL 树 AVL 树的性能
SXF python
aaaqqq1234的博客
09-17 350
闭包 嵌套函数，第二层函数引用了第一层函数的变量，且返回的是第二层函数名。 装饰器 在不改变原函数情况下进行功能扩展。 这个不改变包括函数内部的逻辑，和函数的调用代码。 只需要在原来函数上方加一个魔术方法。 import time def time_it(func): def inner(): start = time.time() func() end = time.time() print(‘用时:{}秒’.format(end-start)) return inner @time_it def fun
评论
添加红包

请填写红包祝福语或标题

个

红包个数最小为10个

元

红包金额最低5元

当前余额3.43元 前往充值 >
需支付：10.00元
成就一亿技术人!
领取后你会自动成为博主和红包主的粉丝 规则
hope_wisdom
发出的红包
实付元
使用余额支付
点击重新获取
扫码支付
钱包余额 0

抵扣说明：

1.余额是钱包充值的虚拟货币，按照1:1的比例进行支付金额的抵扣。
2.余额无法直接购买下载，可以购买VIP、付费专栏及课程。

余额充值