Day06双向链表

原创已于 2022-11-09 08:46:35 修改 · 434 阅读

0 ·

CC 4.0 BY-SA版权

文章标签：

#链表 #数据结构

于 2022-10-29 11:58:05 首次发布

本文围绕双向链表展开，介绍了其定义，即节点保存前后节点地址，能找直接后继和前驱。阐述了双向链表的结构体设计，详细讲解了初始化、插入、删除等功能的实现，包括各操作中指针域的修改情况及特殊情况处理，最后留了双向循环链表的思考题。

定义

每一个节点不仅保存着下一个节点的地址，还存在一个指针域保存上一个节点的地址

意义

每一个节点既可以找到直接后继又可以找到直接前驱

双向链表的结构体设计

typedef int ELEM_TYPE;
typedef struct DNode{
    ELEM_TYPE data;//数据域
    struct DNode *next;//后继
    struct DNode *prior;//前驱
}DNode,*PDNode;

双向链表实现的功能

初始化

void Init_dlist(PDNode pdlist){
    assert(Pdlist!=NULL);
    pdlist->next=NULL;
    pdlist->prior=NULL;
}

初始化状态下，头结点的next和prior都是NULL；

图表解释

头插

bool Insert_head(PDNode pdlist,ELEM_TYPE val){
    assert(Pdlist!=NULL);
    struct Node*pnewnode=(struct Node*)malloc(sizeof(struct Node));
    assert(pnewnode!=NULL);
    pnewnode->data=val;
    pnewnode->next=pdlist->next;
    pnewnode->prior=pdlist;
    if(pdlist->next!=NULL){
        pdlist->next->prior=pnewnode;
    }
    pdlist->next=pnewnode;
    return true;
}

注意事项

1.因为是头插直接使用pdlist头结点即可

2.一共有4个指针域受到影响

自身的prior域，next域，头结点的next域，有效节点的prior域

图表解释

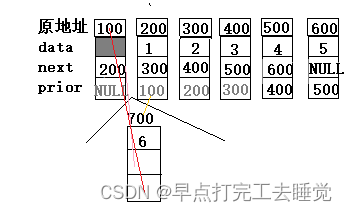
3.修改的先后顺序(不唯一，但是头结点的next需要在最后一个修改)

first.自身的prior域，

second.自身的next域，

third.有效节点的prior域，(存在特殊情况：空链表)

forth.头结点的next域，

尾插

bool Insert_tail(PDNode pdlist,ELEM_TYPE val){
    assert(Pdlist!=NULL);
    struct Node*pnewnode=(struct Node*)malloc(sizeof(struct Node));
    assert(pnewnode!=NULL);
    pnewnode->data=val;
    struct DNode*p=pdlist;
    for(;p!=NULL;p=p->next);
    pnewnode->next=p->next;
    pnewnode->prior=p;
    p->next=pnewnode;
    free(p);
    return true;
}

不存在特例，只需要修改三个指针域：自身的next,prior，尾结点的next域

按位置插

bool Insert_pos(PDNode pdlist,int pos,ELEM_TYPE val){
    assert(Pdlist!=NULL);
    assert(pos>=0&&pos<=GetLenth(pdlist));
    if(pos==0){
       return  Insert_head(pdlist,val);
    }else if(pos==GetLength(pdlist)){
       return  Insert_tail(pdlist,val);
    }
    else{
        strcut Node *pnewnode=(strcut Node*)malloc(strcut Node);
        struct Node*p=plist;
        for(int i=0;i<pos;i++){
            p=p->next;
        }
        pnewnode->data=val;
        pnewnode->next=p->next;
        pnewnode->prior=p;
        p->next->prior=pnewnode;
        p->next=pnewnode;
        
    }
    return true;
}

图表解释

pos==0:头插有特例修改三个指针域

pos==length:尾插修改三个指针域

pos>0&&pos<length:中间位置插入修改四个指针域

头删

也存在特例

bool Del_head(PDNode pdlist){
    assert(Pdlist!=NULL);
    if(IsEmpty(pdlist)){
        return false;
    }
    struct Node*p=pdlist->next;
    pdlist->next=p->next;
    if(p->next!=NULL)//判断待删除节点的下一个节点是否存在
    {
        p->next->prior=pdlist;
    }
    //因为是头删，待删除节点的上一个节点是头结点
    //存在特例只需要修改一个指针域
    free(p);
    return true;
    
}

图表解释

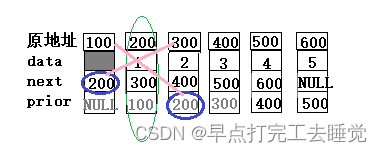
正常情况下进行头删，需要修改两个指针域

1.待删除节点的上一个节点的next域

2.待删除节点的下一个节点的prior域

注意事项：

头删时，删除的是仅剩下的唯一一个节点

这个时候只需要修改待删除节点的上一个节点的next域即可

尾删

bool Del_tail(PDNode pdlist){
    assert(Pdlist!=NULL);
    if(IsEmpty(pdlist)){
        return false;
    }
    struct DNode*p=pdlist;
    for(;p!=NULL;q=q->next);
    struct DNode*q=pdlist;
    for(;q!=p;q=q->next);
    q->next=p->next;
    free(p);
    return true;
}

图表原理

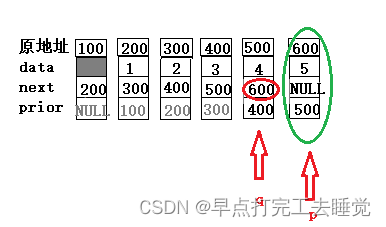
尾删不存在特殊情况，待删除节点为尾结点，所以只有待删除节点的上一个节点存在，待删除节点的下一个节点不存在,只需要待删除节点的上一个节点的next域

按位置删

bool Del_pos(PDNode pdlist,int pos){
    assert(Pdlist!=NULL);
    assert(pos>=0&&pos<GetLength(pdlist));
    if(IsEmpty(pdlist)){
        return false;
    }
    struct DNode*q=pdlist;
    for(int i=0;i<pos;i++){
        q=q->next;
    }
    struct DNode *p=q->next;
    q->next=p->next;
    free(p);
    return true;
    
}

定义两个指针，一个指向待删除节点，一个指向待删除节点的上一个节点。

顺序：

按值删

bool Del_val(PDNode pdlist,ELEM_TYPE val){
    assert(Pdlist!=NULL);
     if(IsEmpty(pdlist)){
        return false;
    }
    struct DNode*p=Search(pdlist,val);
    if(p==NULL){
        return false;
    }//保证待删除节点存在且用p 指向
     struct DNode*q=pdlist;
    for(;p->next!=p;q=q->next);
    //可能存在特例，比如删除为尾结点
    if(p->next==NULL)//代表尾结点
    {
        q->next=p->next;
    }
    else//不是尾结点
    {
        q->next=p->next;
        p->next->prior=q;
    }
    free(p);
    return true;
   
}

查找

struct DNode *Search(PDNode pdlist,ELEM_TYPE val){
    assert(Pdlist!=NULL);
    struct DNode*p=pdlist->next;
    for(;p!=NULL;p=p->next){
        if(p->data==val){
            return p;
        }
    }
    return NULL;
}

销毁

void Destory1(PDNode pdlist){
    assert(Pdlist!=NULL);
    while(!IsEmpty(pdlist)){
        Del_head(pdlist);
    }
}//无限头删
void Destory2(PDNode pdlist){
    assert(Pdlist!=NULL);
    struct DNode*p=pdlist->next;
    pdlist->next =NULL;
    struct DNode*q;
    while(p!=NULL){
        q->next=p->next;
        free(p);
        p=q;
    }
}//利用两个指针完成

清空

void clean(PDNode pdlist){
    assert(Pdlist!=NULL);
    Destory (pdlist);
}

判空

bool IsEmpty(PDNode pdlist){
    assert(Pdlist!=NULL);
    return pdlist->next==NULL;
}

获取有效值个数

int GetLength(PDNode pdlist){
    assert(Pdlist!=NULL);
    int count=0;
    struct DNode*p=pdlist->next;
    for(;p!=NULL;p=p->next){
        count++;
    }
    return count;
}

打印

void Show(PDNode pdlist){
        assert(Pdlist!=NULL);
    int count=0;
    struct DNode*p=pdlist->next;
    for(;p!=NULL;p=p->next){
       printf("%d",p->data);
    }

}

从按值删后原理与Day04的单链表的原理差不多，大家有什么不明白的地方可以去Day04单链表去看看，小白在这给大家留一个思考题双向循环链表该如何设计，它与双向链表有什么区别，我们下期见。