hdu 2364 Escape【模拟优先队列】【bfs】

最新推荐文章于 2025-05-25 15:42:57 发布

原创最新推荐文章于 2025-05-25 15:42:57 发布 · 245 阅读

0 ·

CC 4.0 BY-SA版权

HDUOJ 同时被 2 个专栏收录

85 篇文章

订阅专栏

ACM--搜索

31 篇文章

订阅专栏

本文介绍了一种迷宫逃脱算法，该算法优先选择转弯路径而非直线前进，并详细解析了实现细节及代码示例。

Escape

Time Limit: 1000/1000 MS (Java/Others) Memory Limit: 32768/32768 K (Java/Others)
Total Submission(s): 1182 Accepted Submission(s): 500

Problem Description

You find yourself trapped in a large rectangular room, made up of large square tiles; some are accessible, others are blocked by obstacles or walls. With a single step, you can move from one tile to another tile if it is horizontally or vertically adjacent (i.e. you cannot move diagonally).
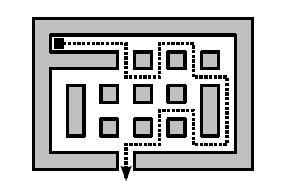
To shake off any people following you, you do not want to move in a straight line. In fact, you want to take a turn at every opportunity, never moving in any single direction longer than strictly necessary. This means that if, for example, you enter a tile from the south, you will turn either left or right, leaving to the west or the east. Only if both directions are blocked, will you move on straight ahead. You never turn around and go back!
Given a map of the room and your starting location, figure out how long it will take you to escape (that is: reach the edge of the room).

Input

On the first line an integer t (1 <= t <= 100): the number of test cases. Then for each test case:

a line with two integers separated by a space, h and w (1 <= h, w <= 80), the height and width of the room;

then h lines, each containing w characters, describing the room. Each character is one of . (period; an accessible space), # (a blocked space) or @ (your starting location).
There will be exactly one @ character in each room description.

Output

For each test case:

A line with an integer: the minimal number of steps necessary to reach the edge of the room, or -1 if no escape is possible.

Sample Input

2
9 13
#############
#@..........#
#####.#.#.#.#
#...........#
#.#.#.#.#.#.#
#.#.......#.#
#.#.#.#.#.#.#
#...........#
#####.#######
4 6
#.####
#.#.##
#...@#
######

Sample Output

31
-1

题意：从唯一的起点‘@’出发，输出到达边界的步数，如果不能到达，输出-1。每走下一步，优先选择转弯的方向，只能直走（两边都是障碍物）时，才选择直走方向，重点是，不能往回走。

判断能否下一步转弯的思路是：先将四个方向用0,1,2,3标记，如果当前步方向和下一步方向相等，当前步方向+1，方向-1，如果这两个方向上同时存在障碍物，说明只能直走，加入队列；如果当前步方向和下一步方向不相等时，直接加入队列。这道题我理解错一个地方，它走过的地方其实可以再走，只是，走过的方向不能再走，所以当我用二维数组标记该点是否走过时，是有问题滴，因为它直接就将四个方向都标记为已经走过，正解应该是，在二维基础上多加一维，用以标记该点的四个方向。

~~~这道题，为什么我先判断只能直走的情况，再判断转弯的情况呢~~因为我对 c++的优先队列并不熟悉，就在函数内部直接判断的时候模拟优先队列操作过程，如果不用优先队列，直接用if(nowq.father!=i)Q.push(nextq);会将除了往回走的方向以外的三个方向直接无序加入，而此题的要求是，优先转弯，不能转弯再直走。

ps:昨天本来想把这道题作为我的双十一大礼包的，结果写了一个下午，都没有写出来，自己好菜啊~~~

#include<stdio.h>
#include<string.h>
#include<queue>
using namespace std;
#define N 85
int map[N][N],mmin,flag,n,m,vis[N][N][4];
char str[N][N];
typedef struct node{
    int x,y;
    int father;//记录方向 
    int step;//记录步数 
}node;

int bfs(int x,int y)
{
    int k[4][2]={0,1,-1,0,0,-1,1,0};
    int nx,ny,xi,yi,x1,y1,x2,y2;
    node nextq,nowq;
    memset(vis,0,sizeof(vis));//初始化标记数组 
    queue<node>Q;
    flag = 0;//标记是否能够成功到达 
    nowq.father = -1;//起点的方向是-1，区别其它点 
    nowq.x = x;
    nowq.y = y;
    nowq.step = 0;//初始化起点 
    vis[x][y][0]=1,vis[x][y][1]=1;//起点标记为已经走过 
    vis[x][y][2]=1,vis[x][y][3] = 1;
    Q.push(nowq);//将起点加入队列 
    while(!Q.empty())
    {
        nowq = Q.front() ;
        Q.pop();
        if(nowq.x == 0||nowq.y == 0||nowq.x == n-1||nowq.y == m-1)//到达出口 
        {
            if(str[nowq.x][nowq.y]!='#')
                flag = 1;//能够成功到达 
            return nowq.step ;
        }
        for(int i = 0; i < 4; i ++)
        {
            nx = nowq.x + k[i][0];
            ny = nowq.y + k[i][1];
            if(nx < 0||ny < 0||nx > n-1||ny > m-1||str[nx][ny]=='#'||vis[nx][ny][i])
                continue;    //不能越界，不能是墙，不能已经是访问过的点 
            nextq.x = nx;
            nextq.y = ny;
            nextq.father = i;//记录父点到当前点的方向 
            nextq.step = nowq.step + 1;//步数加1 
             if(nowq.father%2 == i%2)
            {
                if(nowq.father == i)
                {
                    x1 = nowq.x + k[(i+1)%4][0];
                    y1 = nowq.y + k[(i+1)%4][1];
                    x2 = nowq.x + k[(i-1+4)%4][0];
                    y2 = nowq.y + k[(i-1+4)%4][1];
                    if(str[x1][y1]!='.'&&str[x2][y2]!='.')//如果当前位置左右两边都不能走即只能直走 
                    {
                        vis[nx][ny][i] = 1;//标记该方向为已经访问过
                        Q.push(nextq);
                    }
                }
            }
            else
            {
                    vis[nx][ny][i] = 1;
                    Q.push(nextq);
            }    
        }
    }
    return -1;
}
int main()
{
    int t,i,j,x,y;
    scanf("%d",&t);
    while(t--)
    {
        scanf("%d%d",&n,&m);
        memset(str,0,sizeof(str));
        for(i = 0; i < n; i ++)
        {
            scanf("%s",str[i]);
            for(j = 0; j < m; j ++)
            {
                if(str[i][j] == '@')//找到起点，存入x,y. 
                {
                    x = i;
                    y = j;
                }
            }
        }
        mmin = bfs(x,y);//返回步数 
        if(flag)//如果能到达出口。输出步数 
            printf("%d\n",mmin);
        else
            printf("-1\n");    //否则输出-1 
        
    }
    return 0;
 }