数据结构-链式前向星

链式前向星存储结构

链式前向星是一种高效的图存储方式，特别适合存储稀疏图：

数据结构组成：

• Edge 结构体：存储边的信息（终点、权重、下一条边索引）
• head[] 数组：每个节点的第一条边的索引
• edges[] 数组：存储所有边的信息

存储原理：

• 每个节点的所有出边通过链表串联
• head[u] 指向从节点u出发的第一条边
• 通过 edges[i].next 遍历该节点的所有出边

#include <iostream>
#include <vector>
#include <queue>
#include <climits>
#include <cstring>
using namespace std;

const int MAXN = 1005;  // 最大节点数
const int MAXM = 10005; // 最大边数
const int INF = INT_MAX;

// 链式前向星结构
struct Edge {
    int to;     // 边的终点
    int weight; // 边的权重
    int next;   // 下一条边的索引
};

class Graph {
private:
    Edge edges[MAXM];  // 存储所有边
    int head[MAXN];    // head[i]表示从节点i出发的第一条边的索引
    int edge_count;    // 当前边的数量
    int n;             // 节点数量
    
    // DFS相关
    bool visited[MAXN];
    
    // Dijkstra相关
    int dist[MAXN];
    bool dijkstra_visited[MAXN];

public:
    Graph(int nodes) : n(nodes), edge_count(0) {
        // 初始化head数组，-1表示没有边
        memset(head, -1, sizeof(head));
        memset(visited, false, sizeof(visited));
        memset(dijkstra_visited, false, sizeof(dijkstra_visited));
        fill(dist, dist + MAXN, INF);
    }
    
    // 添加有向边
    void addEdge(int from, int to, int weight) {
        edges[edge_count].to = to;
        edges[edge_count].weight = weight;
        edges[edge_count].next = head[from];  // 链接到之前的边
        head[from] = edge_count;              // 更新头指针
        edge_count++;
    }
    
    // 添加无向边（两条有向边）
    void addUndirectedEdge(int u, int v, int weight) {
        addEdge(u, v, weight);
        addEdge(v, u, weight);
    }
    
    // 打印图的邻接表表示
    void printGraph() {
        cout << "\n=== 图的邻接表表示 ===" << endl;
        for (int i = 1; i <= n; i++) {
            cout << "节点 " << i << ": ";
            for (int j = head[i]; j != -1; j = edges[j].next) {
                cout << "(" << edges[j].to << "," << edges[j].weight << ") ";
            }
            cout << endl;
        }
    }
    
    // DFS深度优先搜索
    void dfs(int u) {
        visited[u] = true;
        cout << u << " ";
        
        // 遍历从节点u出发的所有边
        for (int i = head[u]; i != -1; i = edges[i].next) {
            int v = edges[i].to;
            if (!visited[v]) {
                dfs(v);
            }
        }
    }
    
    // DFS搜索入口
    void dfsSearch(int start) {
        cout << "\n=== DFS搜索结果（从节点" << start << "开始）===" << endl;
        memset(visited, false, sizeof(visited));
        cout << "访问顺序: ";
        dfs(start);
        cout << endl;
    }
    
    // Dijkstra最短路径算法
    void dijkstra(int start) {
        cout << "\n=== Dijkstra最短路径（从节点" << start << "开始）===" << endl;
        
        // 初始化
        fill(dist, dist + MAXN, INF);
        memset(dijkstra_visited, false, sizeof(dijkstra_visited));
        dist[start] = 0;
        
        // 使用优先队列优化
        priority_queue<pair<int, int>, vector<pair<int, int>>, greater<pair<int, int>>> pq;
        pq.push({0, start}); // {距离, 节点}
        
        while (!pq.empty()) {
            int d = pq.top().first;
            int u = pq.top().second;
            pq.pop();
            
            if (dijkstra_visited[u]) continue;
            dijkstra_visited[u] = true;
            
            // 遍历从节点u出发的所有边
            for (int i = head[u]; i != -1; i = edges[i].next) {
                int v = edges[i].to;
                int weight = edges[i].weight;
                
                if (!dijkstra_visited[v] && dist[u] + weight < dist[v]) {
                    dist[v] = dist[u] + weight;
                    pq.push({dist[v], v});
                }
            }
        }
        
        // 输出结果
        cout << "到各节点的最短距离:" << endl;
        for (int i = 1; i <= n; i++) {
            cout << "到节点" << i << ": ";
            if (dist[i] == INF) {
                cout << "不可达" << endl;
            } else {
                cout << dist[i] << endl;
            }
        }
    }
    
    // 朴素Dijkstra实现（不使用优先队列）
    void dijkstraNaive(int start) {
        cout << "\n=== 朴素Dijkstra算法（从节点" << start << "开始）===" << endl;
        
        // 初始化
        fill(dist, dist + MAXN, INF);
        memset(dijkstra_visited, false, sizeof(dijkstra_visited));
        dist[start] = 0;
        
        for (int count = 0; count < n; count++) {
            // 找到未访问的距离最小的节点
            int u = -1;
            for (int i = 1; i <= n; i++) {
                if (!dijkstra_visited[i] && (u == -1 || dist[i] < dist[u])) {
                    u = i;
                }
            }
            
            if (u == -1 || dist[u] == INF) break;
            
            dijkstra_visited[u] = true;
            
            // 更新相邻节点的距离
            for (int i = head[u]; i != -1; i = edges[i].next) {
                int v = edges[i].to;
                int weight = edges[i].weight;
                
                if (!dijkstra_visited[v] && dist[u] + weight < dist[v]) {
                    dist[v] = dist[u] + weight;
                }
            }
        }
        
        // 输出结果
        cout << "到各节点的最短距离:" << endl;
        for (int i = 1; i <= n; i++) {
            cout << "到节点" << i << ": ";
            if (dist[i] == INF) {
                cout << "不可达" << endl;
            } else {
                cout << dist[i] << endl;
            }
        }
    }
};

int main() {
    // 创建一个5个节点的图
    Graph g(5);
    
    // 添加有权边 (无向图)
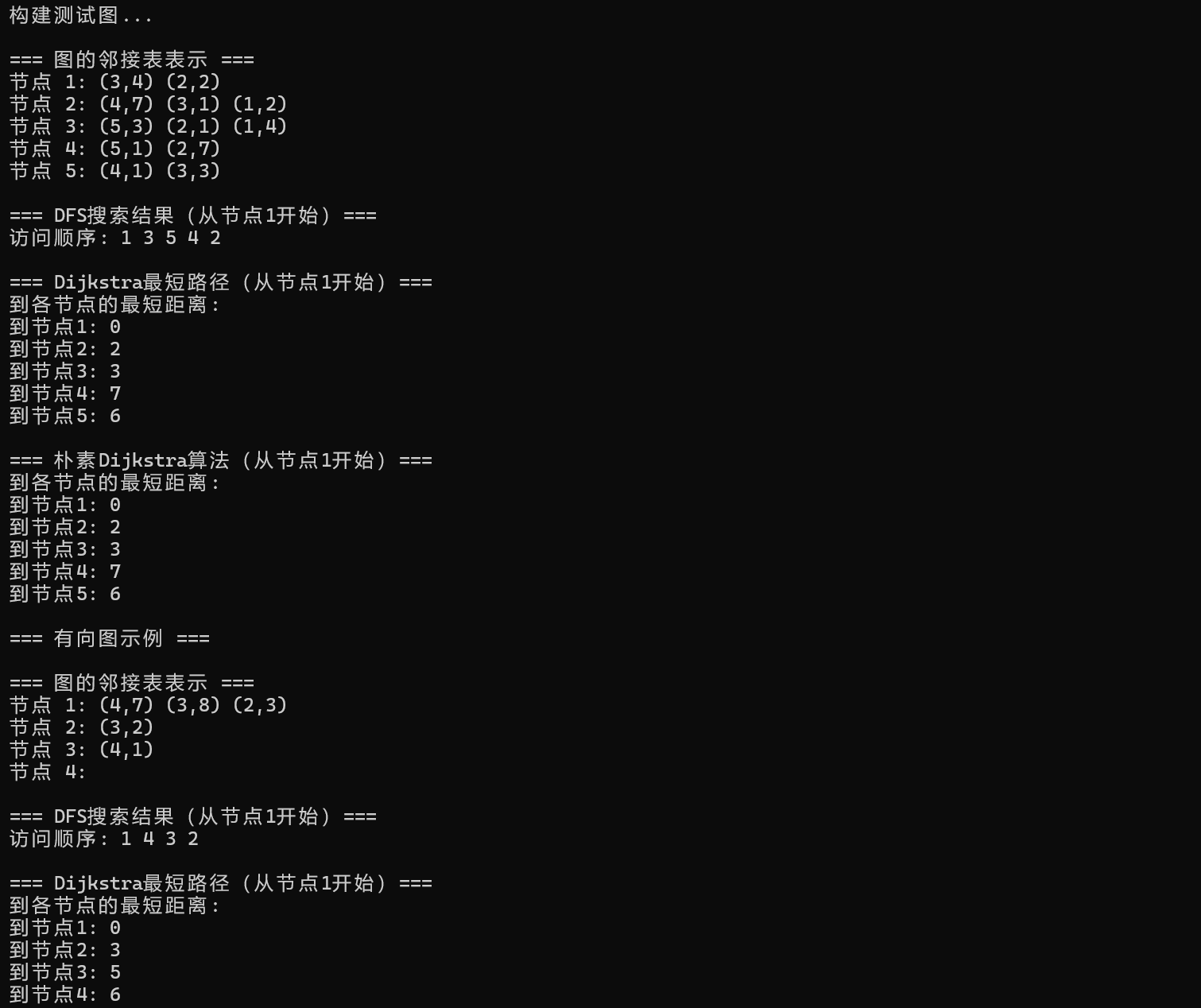
    cout << "构建测试图..." << endl;
    g.addUndirectedEdge(1, 2, 2);
    g.addUndirectedEdge(1, 3, 4);
    g.addUndirectedEdge(2, 3, 1);
    g.addUndirectedEdge(2, 4, 7);
    g.addUndirectedEdge(3, 5, 3);
    g.addUndirectedEdge(4, 5, 1);
    
    // 打印图结构
    g.printGraph();
    
    // 执行DFS搜索
    g.dfsSearch(1);
    
    // 执行Dijkstra算法（优先队列版本）
    g.dijkstra(1);
    
    // 执行朴素Dijkstra算法
    g.dijkstraNaive(1);
    
    cout << "\n=== 有向图示例 ===" << endl;
    Graph directed_g(4);
    directed_g.addEdge(1, 2, 3);
    directed_g.addEdge(1, 3, 8);
    directed_g.addEdge(1, 4, 7);
    directed_g.addEdge(2, 3, 2);
    directed_g.addEdge(3, 4, 1);
    
    directed_g.printGraph();
    directed_g.dfsSearch(1);
    directed_g.dijkstra(1);
    
    return 0;
}