题目描述:
输入一颗二叉树和一个整数,打印出二叉树中结点值的和为输入整数的所有路径。路径定义为从树的根结点开始往下一直到叶结点所经过的结点形成一条路径。
思想:
利用树的先序遍历访问所有结点,先将当前结点存储,然后更新target为target-root.val,继续递归访问其左右子树即可。如果到达叶子结点的时候,target==0,则当前路径即为所求路径
import java.util.ArrayList;
class TreeNode{
int val;
TreeNode left;
TreeNode right;
TreeNode(int x){
val = x;
}
}
public class test1 {
public static ArrayList<ArrayList<Integer>> res = new ArrayList<ArrayList<Integer>>();
public static ArrayList<Integer> list = new ArrayList<Integer>();
public static void findPath(TreeNode root, int target) {
if(root == null)
return;
//先序遍历,先存储根节点
list.add(root.val);
//更新target,因为已经保存当前节点的值了,所以接下的目标值就是target-root.val
target -= root.val;
//如果当前结点为叶子节点,且target为0,说明当前路径符合要求,保存
if(target == 0 && root.left == null && root.right == null)
//这个地方一定要新建对象实例
res.add(new ArrayList<Integer>(list));
findPath(root.left, target);
findPath(root.right, target);
//回溯,因为当前节点已经访问过了,下一次遍历路径不应该包含当前节点了
list.remove(list.size() - 1);
}
public static void main(String[] args) {
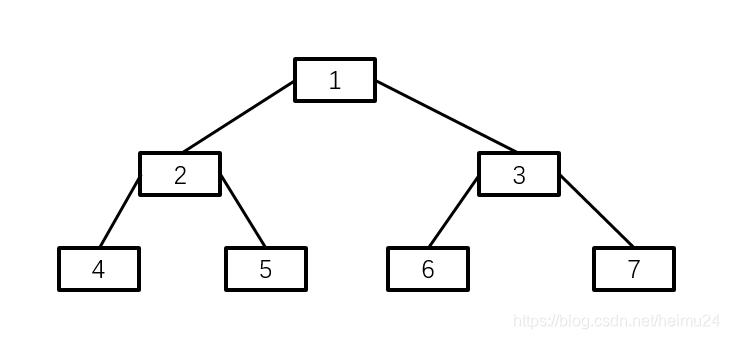
TreeNode root = new TreeNode(1);
root.left = new TreeNode(2);
root.right = new TreeNode(3);
root.left.left = new TreeNode(4);
root.left.right = new TreeNode(5);
root.right.left = new TreeNode(6);
root.right.right = new TreeNode(7);
int target = 7;
findPath(root, target);
System.out.println(res);
}
}
输入:
打印结果
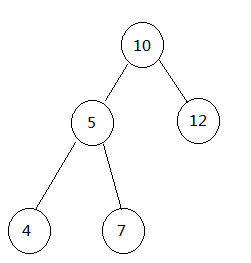
具体遍历及回溯过程如下(来源参考链接)
二叉树root, target = 22
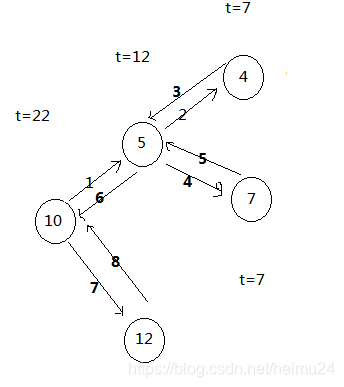










 本文介绍了一种算法,用于查找二叉树中所有路径的节点值之和等于特定整数的路径。通过先序遍历的方式,递归地访问每个节点,更新目标值并检查是否达到叶子节点且目标值为零,以确定路径是否符合要求。
本文介绍了一种算法,用于查找二叉树中所有路径的节点值之和等于特定整数的路径。通过先序遍历的方式,递归地访问每个节点,更新目标值并检查是否达到叶子节点且目标值为零,以确定路径是否符合要求。
















 2379
2379

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








