文章目录
导数
导数引告
导数描述的是变化率, 我们使用生活中的例子进行举例.
例如: 冬天中, 水杯0s - 10s从 100° - 0° 的变化.

平均每1秒, 温度变化多少?
那么公式会变为这样:

此时我们得到了平均变化率, 此时我们应该知道, 第3秒的时候水温变化了多少. 但是我们却不知道3.5秒, 0.8时, 温度瞬间变为多少.
导数的定义
通过上面的例子我们知道.
时间: 0s -> 10s
温度: 0° -> 100°
温度平均变化率: (100° - 0°) / (10s - 0s) = 10°/s
那么如果有个问题, 在第2秒时, 温度瞬间变为多少, 此时我们就应该引入极限.

当然了, 生活中除了这个温度变化率, 当然还有山坡陡峭等其他例子, 这里不做其他演示. 在数学中, 我们用函数来进行计算.
函数的导数
定义式
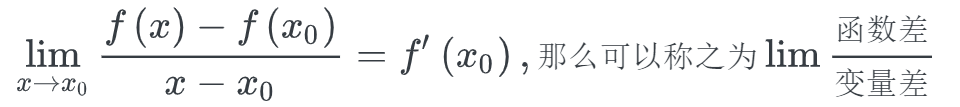
增量式
这里我们引入一个概念

△x如何理解呢, 我们可以看一下数轴:
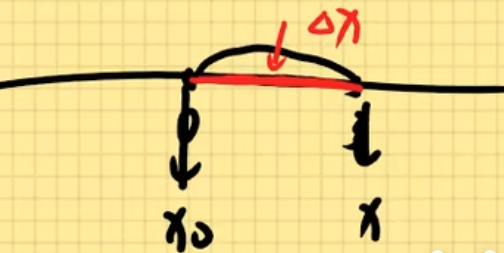
其实也就是x-x0的差值, 不难理解, 那么带入到我们之前的公式后变为了:

注:
- △x可以换成其余字母 h t 等.
- 整体思想, △x 可以替换为 □
- 谁趋向于0, 谁就是 △x
引申公式

增量式例题
例题1&解题 (增量式)
题目:

解题:

例题2&解题 (引申公式)
题目:

解题:

例题3&解题 (引申公式)

例题4&解题 (引申公式)

例题5&解法 (详细)

定义式例题
例题1&解题 (利用定义式)

图中利用了定义式, 将结果算出.
例题2&解题 (利用定义式)

例题3&解题

极限得出常数项, 则分母趋0, 分子也趋0. 将a带入发现分母是零比零型, 所以f(x)等于0.
定义式建立极限关系
例题1&解法 (拼凑法)
题目:

解题:

例题2&解法

解题思路大同小异.
左右导数定义
导数定义

理解: 导数源于极限, 极限存在则是左右极限相等, 而导数存在, 也对应了左右导数相等
函数在某点x0可导条件:

可导的必要条件: 可导函数必连续, 连续必极限存在.
理解

为什么尖点处不可导: 因为尖点处的切线可以做任意多个, 所以不可导.
做题技巧: 如果函数加上了绝对值, 那么就会产生尖点(绝对值函数的零点), 就不可导了.
例题1&解法

解题应用
这里记载一下遇到"可导"两个字眼的思考方向:

例题1&解法
题目:

解法:

例题2&解法
题目:

解法:

不可导情况 (了解)
不可导的情况有两种
左导≠右导
导数为∞
例题1&解法

这里需要注意绝对值问题, 当趋向于0的右侧时, 我们可以模拟的将绝对值看为0.xxx, 然后来判断绝对值的正负号, 当倾向于0的左侧时, 我们可以模拟的将绝对值看为-0.xxx.
例题2&解法

解题上大同小异, 绝对值表达式的正负根据1的左侧右侧来判断. 左导数与右导数不相等, 那么不可导.
例题3&解法

例题4&解法

导数四则运算, 复合运算法则
各大类函数的求导公式
常数函数
[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-eun1owZd-1681644028423)(C:\Users\Heihu577\AppData\Roaming\Typora\typora-user-images\image-20220929083748528.png)]
任何一个常数求导, 都等于0.
幂函数

指数
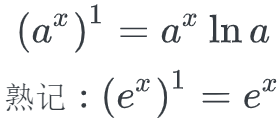
对数

三角函数

反三角函数

四则运算

拓展 (了解即可): (uvw)’ = u’vw + uv’w + uvw’
补充: dy/dx & f’(x) 的关系

例题1&解法

例题2&解法

复合运算
原则: 从外向里, 层层求导, 每层相乘.
例题1&解法

初等函数求导
例题1&解法

例题2&解法

复合函数求导
例题1&解法

例题2&解法
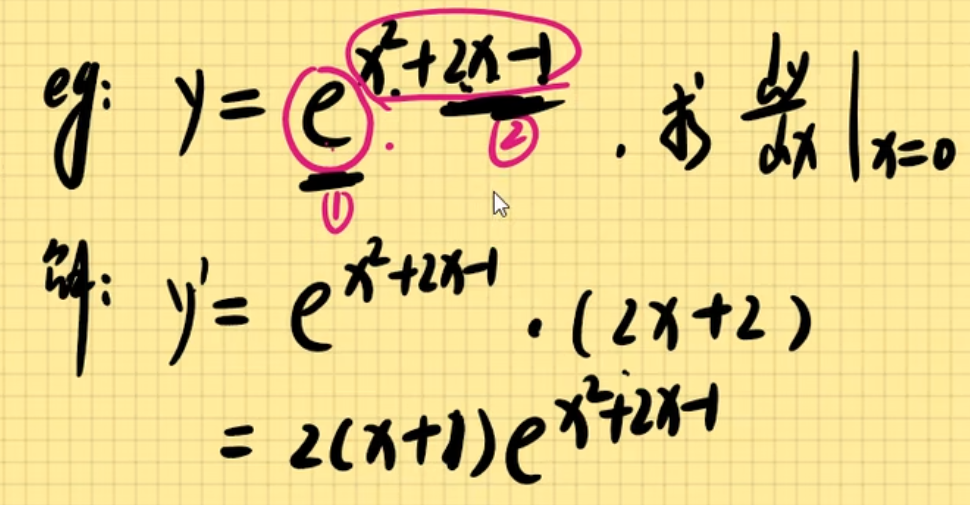
例题3&解法

抽象函数求导
例题1&解法

例题2&解法 (经典)

复合函数常见公式
当我们对一个复杂表达式求导时, 尽可能去化简它, 常见公式如下:

尽可能的避免分式求导.
例题1&解法

例题2&解法 (经典)
题目:

解法:

各类函数求导 (另类)
分段函数求导
求导原则:
- 分段点两侧, 直接求导
- 中间分段点处, 用定义求导
可导 = 可微
例题1&解法
题目:

解法:

答案选D.
例题2&解法
题目:

解法: 左极限右极限求出b, 左导右导求出a
隐函数求导
隐函数定义
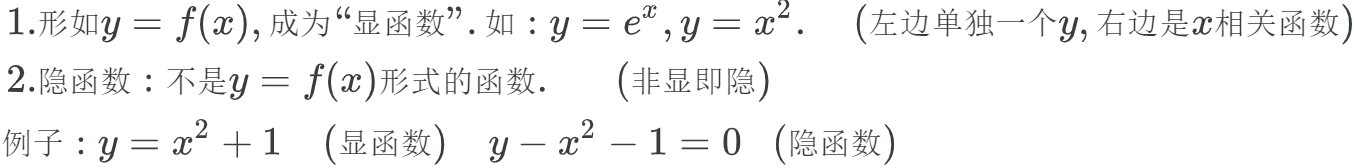
解法
公式法

正规解法
将 y 看为 y(x), 然后使用复合函数求导法则即可.如图:

例题1&解法
题目:

解法:
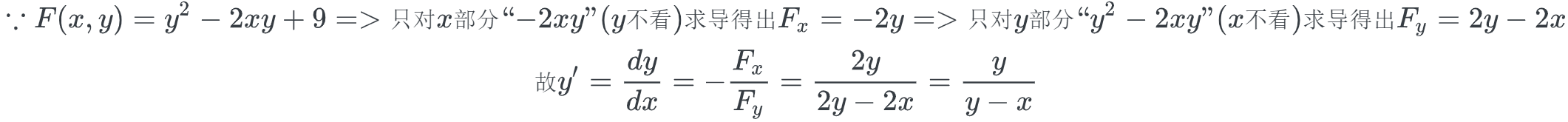
例题2&解法

例题3&解法 (经典)
题目:

解法:

例题3&解法
题目:

解法:

例题5&解法 (经典)

例题6&解法 (必看)

例题7&解法 (必看)

参数方程求导
参数方程定义
定义: x与y通过中间变量t, 间接建立的函数关系式.

求导原则

原理

例题1&解法
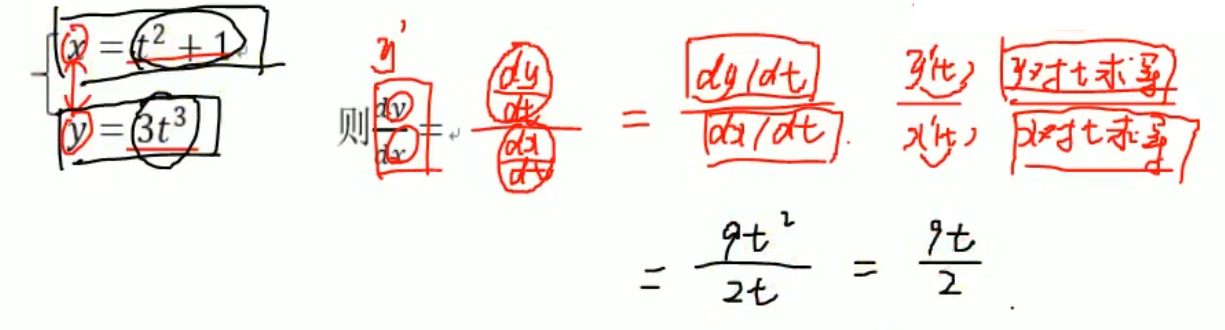
例题2&解法 (必看)

例题3&解法 (必看)

例题1&解法

例题2&解法 (经典)
题目:

解法:

例题3&解法 (隐函数+参数方程)
题目:

解法:

幂指函数求导
例如:

称为幂指函数, 它有自己独立一套的求导方法.
求导方法
对数求导法
-
遇到
幂指函数, 例如:
-
等式两边
同时取对数, 如图:
-
对两边同时求导. (前者是复合函数, 后者是乘法求导公式)

图中等式后边存在错误, 应该是
u'lnv+u(lnv)', 前导后不导, 前不导后导. -
因为左边存在y分之1, 那么等式两边同乘y

图中等式后边存在错误, 注意前面两项需要加上括号.
-
将y等式右边的y替换成原式

简单例题1&解法

例题2&解法 (经典)
题目:

解题:

公式变形法

简单例题1&解法

两种方法的选择

例题1&解法

例题2&解法

变限积分求导
定义

求导方法

例题1&解法 (简单)

例题2&解法 (经典错误)

针对考题

例题1&解法
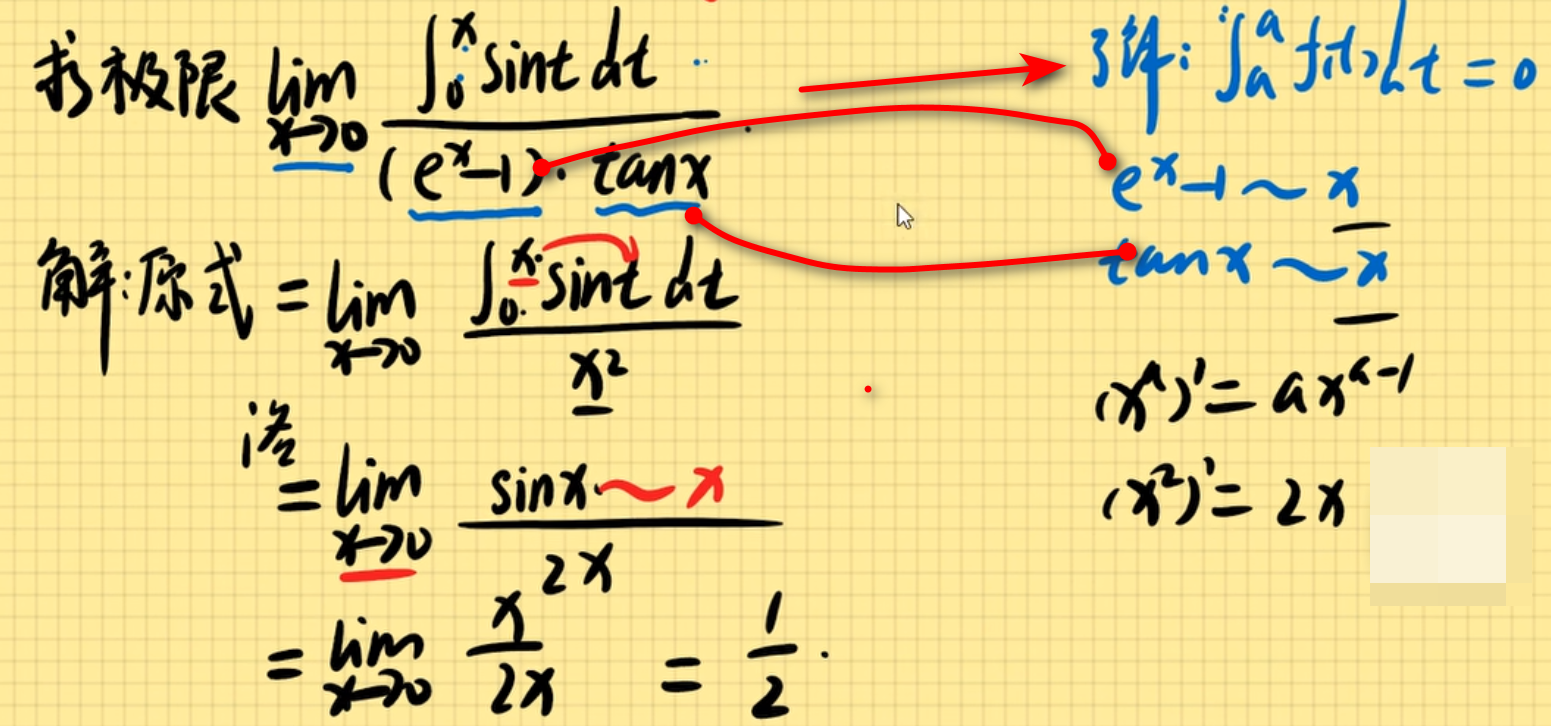
高阶导数
河北大纲: 会求某些简单函数的 n 阶导数.
定义

拓展

题型及解法
题型一: 求具体导数
例题1&解法 (引子)

通过这道题我们可以得出:

拓展:

例题2&解法 (经典)

例题3&解法

例题大总汇

题型二: 求n阶导数表达式
这类题目的解法为: 求2次或3次导数, 找规律. 遇到sin或cos或分式使用现有的公式.
例题1&解法

例题2&解法 (三角函数n阶公式)

例题3&解法 (分式)

函数的微分
函数微分的概念

微分的另一种形式

例题1&解法

例题2&解法

例题总结

导数的几何应用
切线的引入
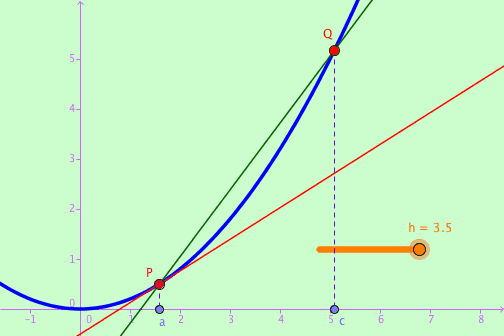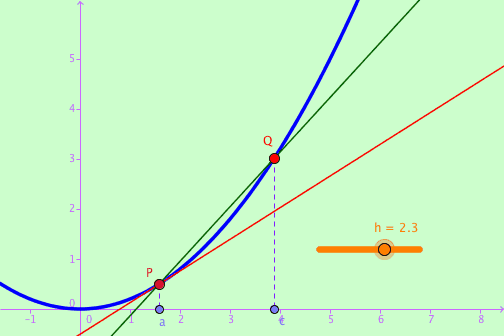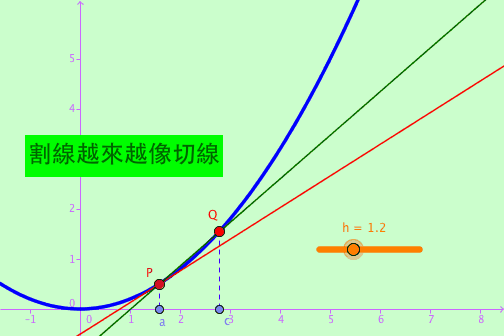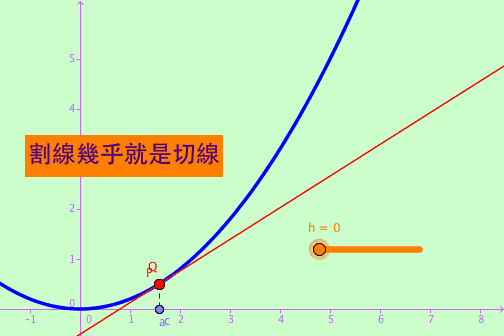
图中蓝色部分为函数图像, Q点是函数上的某一点例如坐标 (x, y), P点也是函数上的某一点 例如坐标 (x0, y0).
我们知道, 两点确定一条直线 (图中Q与P最初的绿色部分), Q与P两点确定的一条线叫做割线.
而在Q趋向于P的过程的最终结果, 会形成一条特有的线 (图中橙色部分), 叫做切线. 那么就诞生了导数函数的最初公式.
定义及公式

题型总结
题型一: 切点[x0, f(x0)] 已知
题目1&解法

题目2&解法
题目:

解法:

例题3&解法 (超详细)

题型二: 切点未知情况
- 设切点为[a, f(a)] 得到切线 y-f(a)=f(a)(x-a)
- 利用题干的切线满足条件算出a的值
题目1&解法

题目2&解法

题目3&解法 (相切导数相同得出)

题目4&解法 (平行求点)

题目5&解法 (外一点, 超详细)

导数确定函数单调性
定义及概念
设 f(x) 在区间 [a, b] 可导, 那么有如下规则:
- 若 f’(x) > 0, 那么 f(x) 在 [a, b] 中为单调增.
- 若 f’(x) < 0, 那么 f(x) 在 [a, b] 中为单调减.
- 若 f’(x0) = 0, 那么称 x0 为
驻点.

理解图2:

例题1&解法 (经典)

得出求导结果后, 我们去查找可能极值点 (驻点, 一阶导不存在的点).

例题2&解法 (小题)

例题3&解法

函数的极值
定义及概念
-
极值: 指f(x)的局部最值
- 极大值: 指局部范围最大值
- 极小值: 指局部范围最小值
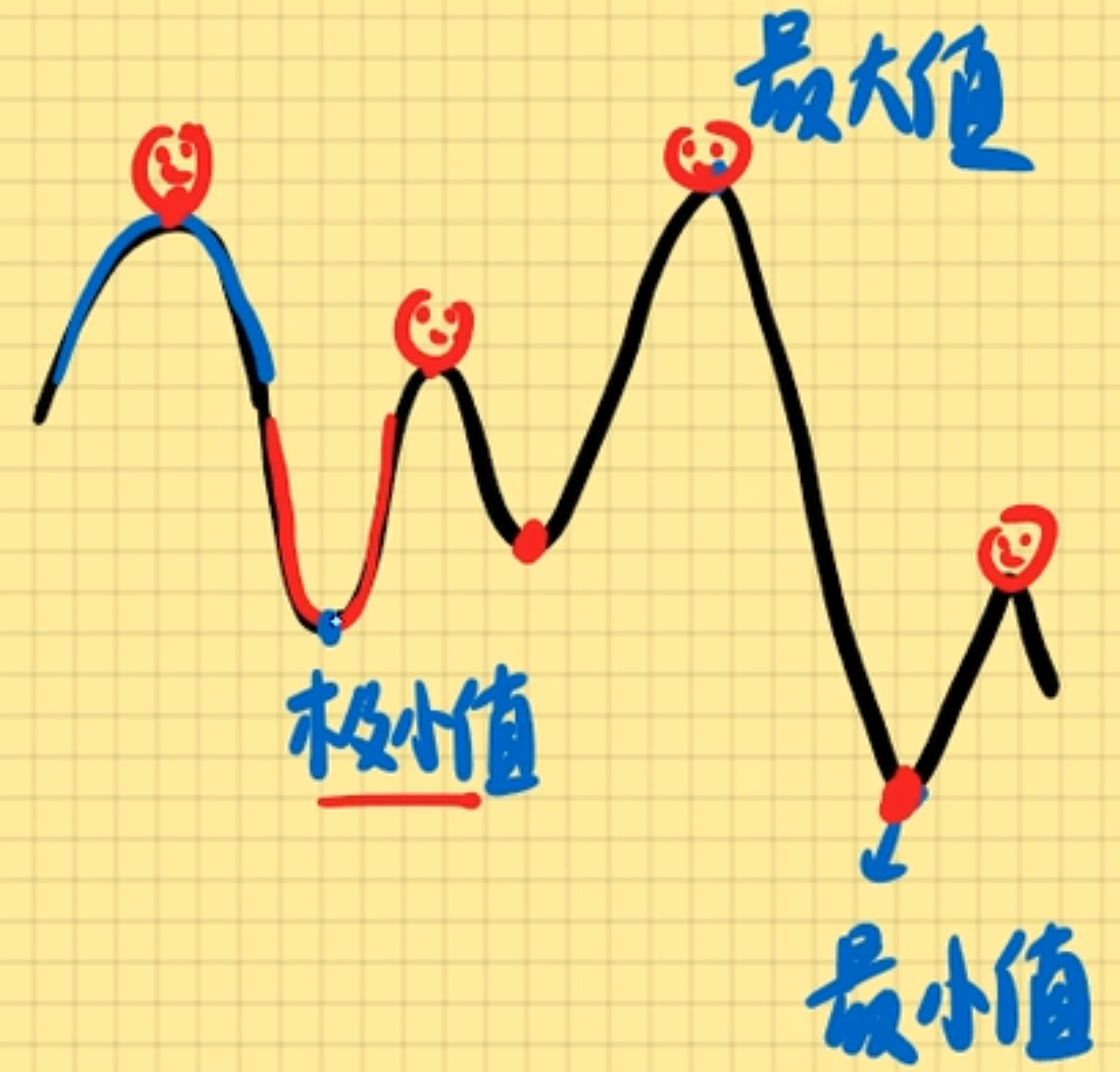
-
极值点的出处
-
f'(x)=0的点 ->(驻点) -
f’(x) 不存在的点
(无定义点)-> 不可导点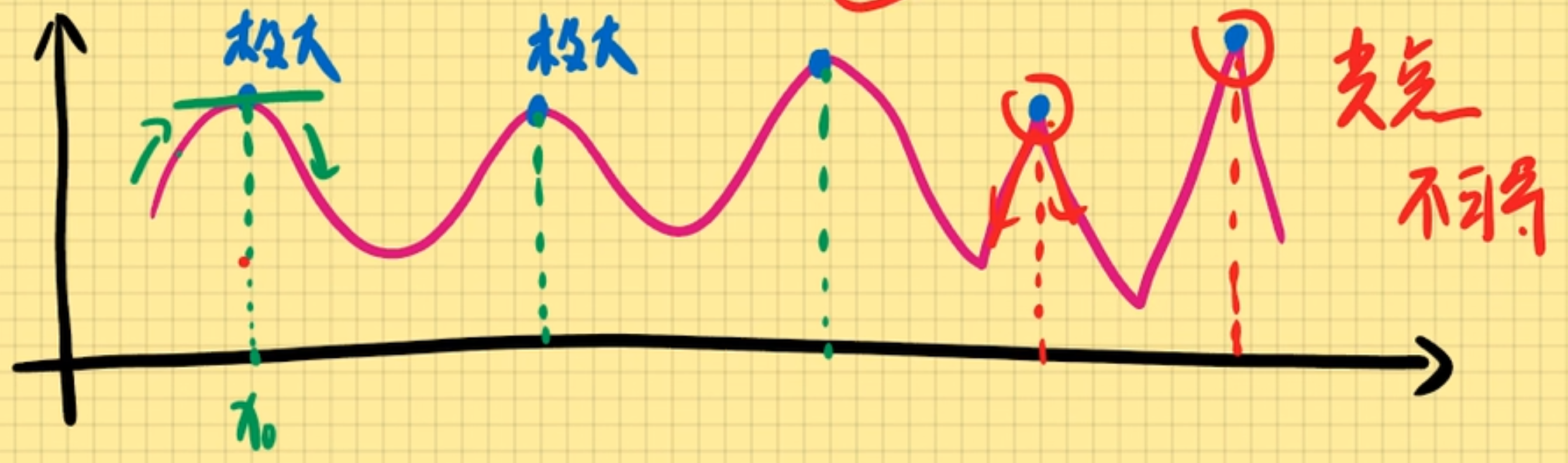
-
-
极值的判断
-
利用
单调性来进行判断 (大题使用较多)-
先增后减为极大值 -
先减后增为极小值
-
-
利用二阶导f’'(x0)判断. (小题使用较多)
- f’'(x0) < 0 则 可以判断出是极大值
- f’'(x0) > 0 则 可以判断出是极小值
-
-
求极值的步骤
- 确定 f(x) 的定义域
- 令 f’(x)=0, 找到驻点, 以及 f(x) 无定义点
- 利用这些点, 分割定义域, 成子区间
- 列表讨论子区间内的单调性, 即 f’(x) 正负性
极大值以及极小值.
题目1&解法

题目2&解法

题目3&解法

题目4&解法

题目5&解法

极值点与驻点的关系

题目1&解法

函数的最值 (低频考点)
定义及概念
在一段函数中, 最高的值叫做最大值, 最低的值叫做最小值.

解法
- 确定f(x)的定义域
- 最大值包括
端点值以及极值, 所以我们将其求出. - 比较以上函数值, 最大的值则是最大值, 最小的值则是最小值.
题目1&解法
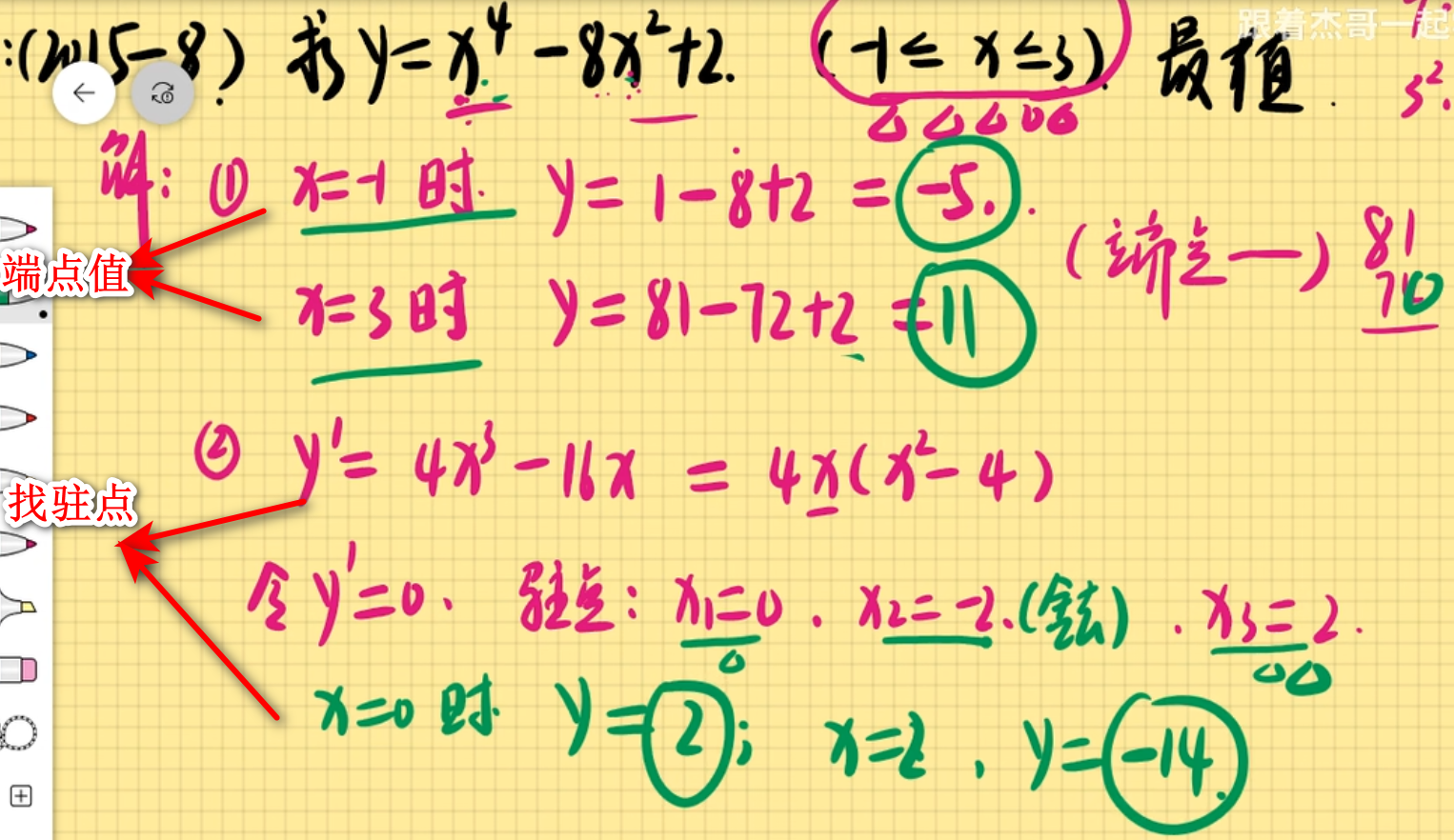
最终结果为, 最大值11, 最小值-14.
题目2&解法
将边长为a的一个正方形铁皮, 四角截去一个大小相同的小正方形, 再将四边形折成一个无盖方盒, 问: 截掉的小正方形边长为多大时, 方盒的容积最大.
画图列出关系式


函数的凹凸性 (二阶导的应用)
定义及概念
曲线的凹凸性可以看如下图:

当然, 我们可以通过二阶导来进行判断:
当 f’'(x) > 0 时, 图像是凹的. (极小值)
当 f’'(x) < 0 时, 图像是凸的. (极大值)
当 f’‘(x) = 0 || f’‘(x) 不存在 时, 判断f’‘(左端)以及f’'(右端)是异号, 则是拐点. 例如:
求解f(x)凹凸区间及拐点.
- 确定f(x)定义域
- 求f’‘(x), 且令f’‘(x)=0, 或f’'(x)不存在的点
- 用这些分割定义域, 讨论子区间f’'(x)正负性, 是凹还是凸
题目1&解法

拐点不存在的情况[例题]

题目&解法 (经典)

题目&解法 (反求)

题目集

罗尔定理 (河北出小题)

例题1&解法

证明题

简单证明题

拉格朗日定理 (河北出小题)

例题1&解法

例题2&解法

例题3&解法

























 1万+
1万+

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








