acwing周赛第一场补题3

将 1∼n 按顺序排成一排，构成一个数列。

数字 i 刚好位于位置 i。

再给定一个长度为 n 的位置序列 p1,p2,…,pn，它是 1∼n 的一种排列。

接下来，我们会重复不断地对数列进行如下操作：

重新排列数列中每个数的位置，将位于位置 i 的数移动至位置 pi。（如果 i=pi 则该数仍移动至位置 i）。
每次操作开始时，所有数的移动同时进行，操作结束后，数列将变为一个新的 1∼n 的排列。
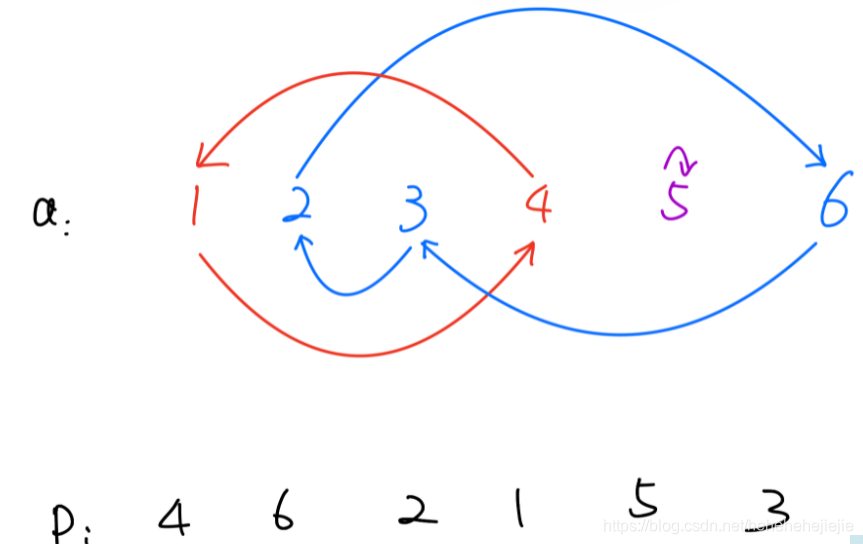
例如，当 n=6 并且 p=[4,6,1,3,5,2] 时，第一次操作后，数字 1 将移动至位置 4，数字 2 将移动至位置 6，以此类推；第二次操作后，数字 1 将移动至位置 3，数字 2 将移动至位置 2，以此类推。

你的任务是确定从 1 到 n 的每个数字 i，经过多少次操作后，第一次重新回到位置 i。

例如，考虑 p=[5,1,2,4,3]，数字 1 的移动轨迹如下：

第一次操作后，到达位置 5。
第二次操作后，到达位置 3。
第三次操作后，到达位置 2。
第四次操作后，回到位置 1。
所以，经过四次操作后，数字 1 第一次回到位置 1。

值得一提的是，数字 4 经过一次操作后就回到了位置 4.

输入格式
第一行包含整数 T，表示共有 T 组测试数据。

每组数据第一行包含整数 n。

第二行包含 n 个整数 p1,…,pn。

输出格式
每组数据输出一行结果，包含 n 个整数，其中第 i 个整数表示数字 i 第一次回到位置 i 所经过的操作次数。

整数之间用单个空格隔开。

数据范围
对于 30% 的数据，1≤T≤10，1≤n≤10。
对于 100% 的数据，1≤T≤1000，1≤n≤2×105，1≤pi≤n。
保证 p1∼pn 是 1∼n 的一种排列。
保证 ∑n≤2×105（一个输入中的 T 个 n 相加之和不超过 2×105）。

输入样例：
6
5
1 2 3 4 5
3
2 3 1
6
4 6 2 1 5 3
1
1
4
3 4 1 2
5
5 1 2 4 3
输出样例：
1 1 1 1 1
3 3 3
2 3 3 2 1 3
1
2 2 2 2
4 4 4 1 4

首先，分析题意，每个点从第一次跳转到最终回到自己，所联结成的路径是一个环，第一次回到原来的位置需要走的步数是这个环上的点的数目，那么第一个思路，我们可以对每一个点dfs一遍求出其所有环上的点，dfs的过程中把在环上的点记录下来，然后这些点的第一次回到原本的位置的所需要的步数都是这个环上的点的数目。

#include<bits/stdc++.h>
using namespace std;

int T;

const int N = 2e5+10;
int n;

int a[N];

bool st[N];
int res[N];
int node[N];
int cnt=0;

int dfs(int x)
{
    if(st[x])return 0;
    st[x]=true;
    node[cnt++]=x;
    return dfs(a[x])+1;
}

int main()
{
    scanf("%d",&T);
    
    while(T--)
    {
        scanf("%d", &n);
        
        for(int i=1;i<=n;i++)scanf("%d",&a[i]);
        
        memset(st,0,sizeof(st));
        memset(res,0,sizeof(res));
        memset(node,0,sizeof(node));
       
       

        
        for(int i=1;i<=n;i++){
            if(!st[i]){
                int t=dfs(i);
                 cnt=0;
                for(int j=0;j<cnt;j++)res[node[j]]=t;
               
            }

        }

        for(int i=1;i<=n;i++)printf("%d ",res[i]);

        cout<<endl;
        
        
    }

   system("pause");
   
    
    return 0;
}

第二种做法，我们发现每一个点的要回到自己的经过的所有点中连接成一个环，我们可以把这个环看成一个连通块，连通块中点的数量就是每一个点第一次经过交换后要到达自己所走过的步数，那么这个点就可以用一个维护连通块中点的数量的并查集来维护。

#include<bits/stdc++.h>
using namespace std;

int T;

const int N = 2e5+10;
int n;

int a[N];
int p[N];
int s[N];
int find(int x)  // 并查集
{
    if (p[x] != x) p[x] = find(p[x]);
    return p[x];
}

int main()
{
    scanf("%d",&T);
    
    while(T--)
    {
        scanf("%d", &n);
        
        for(int i=1;i<=n;i++)scanf("%d",&a[i]);
        
        for(int i=1;i<=n;i++)p[i]=i,s[i]=1;
        
        for(int i=1;i<=n;i++)
        {
            if(find(a[i])!=find(i))
            {
                s[find(a[i])]+=s[find(i)];
                p[find(i)]=find(a[i]);
            }
        }
        
        for(int i=1;i<=n;i++)printf("%d ",s[find(i)]);
        
        
        cout<<endl;
        
        
    }
    
    return 0;
}