C语言 四边形的最大面积(Maximum area of quadrilateral)

给定四边形a, b, c, d的四条边，根据给定的边数求四边形的最大面积。

例子： 

输入：1 2 1 2

输出：2.00

构造一个矩形以获得最大面积是最佳的。

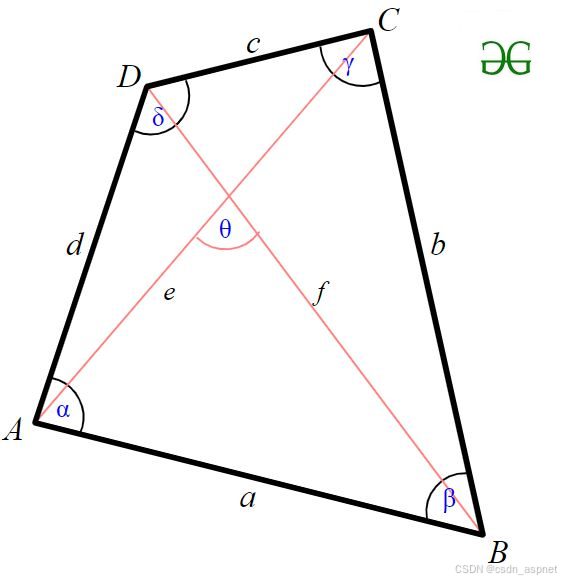
根据Bretschneider 公式，一般四边形的面积为，K=

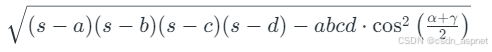
这里，a、b、c、d 是四边形的边长，s 是四边形的半周长，角是两个对角。 
因此，只有当对角和等于 π(180) 时，该公式才最大化。然后，我们可以使用 Bretschneider 公式的简化形式来计算（最大）面积 K。

这个公式被称为Brahmagupta 公式。 
 

下面是给定方法的实现：

// CPP program to find maximum area of a 
// quadrilateral
#include <stdio.h>
#include <math.h>
 
double maxArea(double a, double b,
                double c, double d)
{
    // Calculating the semi-perimeter 
    // of the given quadrilateral
    double semiperimeter = (a + b + c + d) / 2;
 
    // Applying Brahmagupta's formula to
    // get maximum area of quadrilateral
    return sqrt((semiperimeter - a) *
                (semiperimeter - b) * 
                (semiperimeter - c) * 
                (semiperimeter - d));
}
 
// Driver code
int main()
{
    double a = 1, b = 2, c= 1, d = 2;
    printf("%.2f\n",maxArea(a, b, c, d));
    return 0;
}

输出：  

2.00

时间复杂度： O(logn) 

辅助空间： O(1)

如果有人有在空间和时间方面更高效的更好解决方案，请提出建议。

如果您喜欢此文章，请收藏、点赞、评论，谢谢，祝您快乐每一天。